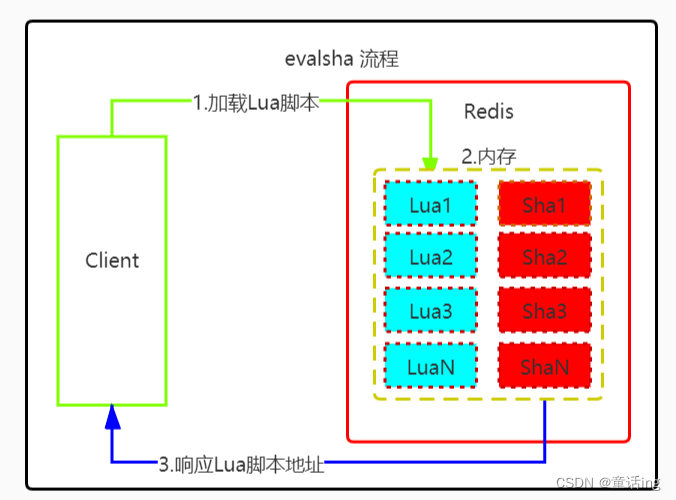
前缀表达式的计算机求值

注意:在前缀表达式中,遇到运算符时,如“-”,是栈顶元素 - 次顶元素
中缀表达式
后缀表达式

 注意:在后缀表达式中,遇到运算符时,如“-”,是次顶元素 - 栈顶元素
注意:在后缀表达式中,遇到运算符时,如“-”,是次顶元素 - 栈顶元素
逆波兰计算器

思路如后缀表达式中的第二张图所示
代码实现如下:
# 用数组模拟栈
class ArrayStack:
def __init__(self, size):
self.max_size = size # 栈的最大容量
self.top = -1 # top 表示栈顶
self.stack = [] # 用列表表示数组
# 判断栈满
def is_full(self):
return self.top == self.max_size - 1
# 判断栈空
def is_empty(self):
return self.top == -1
# 入栈
def push(self, ele):
if self.is_full():
print("栈已满")
else:
self.top += 1
self.stack.insert(self.top, ele)
# 出栈
def pop(self):
if self.is_empty():
print("栈空")
else:
val = self.stack.pop(self.top)
self.top -= 1
return val
# 实现逆波兰表达式
def poland(expression: str):
# 以空格分割输入的逆波兰表达式
str_list = expression.split(" ")
# 创建操作数栈
num_stack = ArrayStack(len(str_list))
operator = {
"+": lambda x, y: x + y,
"-": lambda x, y: x - y,
"*": lambda x, y: x * y,
"/": lambda x, y: x / y
}
# 从左往右遍历逆波兰式列表
for i in str_list:
try:
i = float(i)
# 遇到数字将其压入操作数栈
num_stack.push(float(i))
except Exception: # 遇到运算符弹出两个操作数进行运算,并将结果压入数栈
# 弹出两个操作数,注意是 次顶元素 运算符(如 -) 栈顶元素
num2 = num_stack.pop()
num1 = num_stack.pop()
res = operator[i](num1, num2)
if res:
# 将运算结果压入栈
num_stack.push(res)
else:
raise ValueError("不支持运算符{}".format(i))
print("运算结果为:", num_stack.pop())
poland("3 4 + 5 * 6 -")
poland("4 5 * 8 - 60 + 8 2 / +")中缀表达式转后缀表达式
思路分析

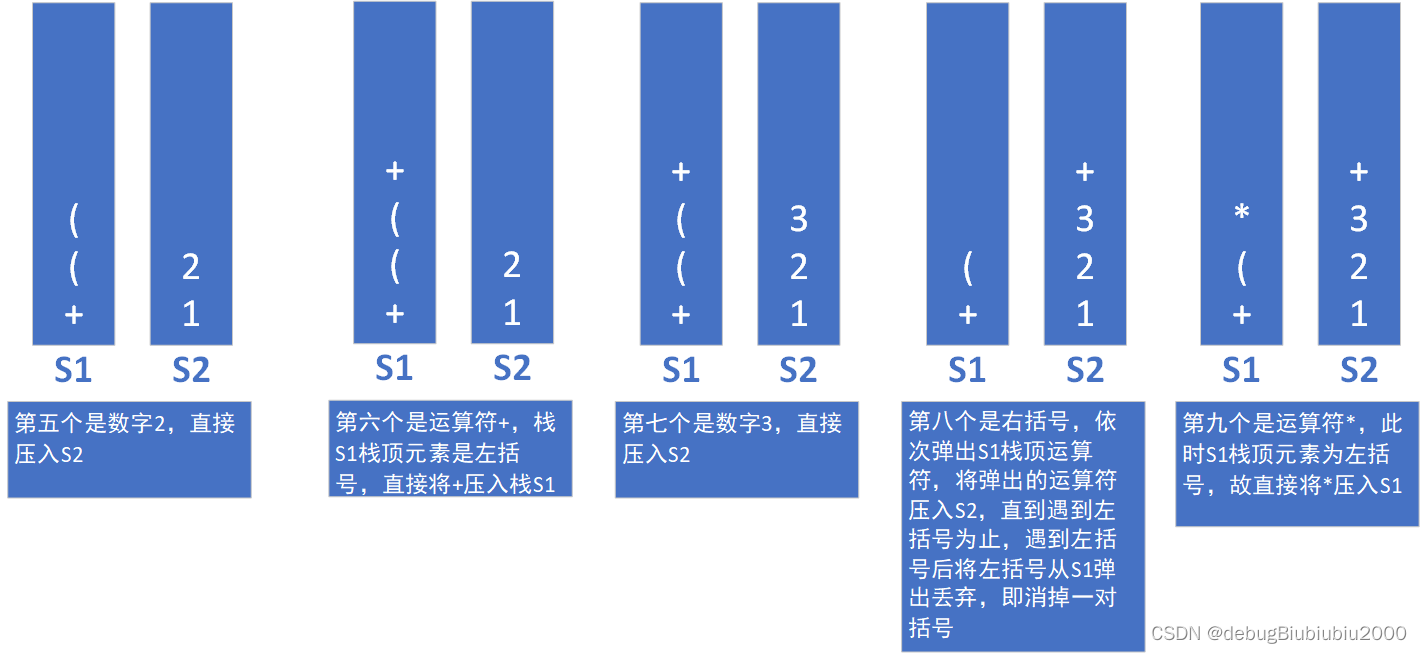
示意图
例子:将中缀表达式:1+((2+3)* 4)-5 转为后缀表达式: 1 2 3 + 4 * + 5 -


代码实现
# 用数组模拟栈
class ArrayStack:
def __init__(self, size):
self.max_size = size # 栈的最大容量
self.top = -1 # top 表示栈顶
self.stack = [] # 用列表表示数组
# 判断栈满
def is_full(self):
return self.top == self.max_size - 1
# 判断栈空
def is_empty(self):
return self.top == -1
# 入栈
def push(self, ele):
if self.is_full():
print("栈已满")
else:
self.top += 1
self.stack.insert(self.top, ele)
# 出栈
def pop(self):
if self.is_empty():
print("栈空")
else:
val = self.stack.pop(self.top)
self.top -= 1
return val
# 查看栈顶元素
def get_top(self):
if self.is_empty():
print("栈空")
else:
return self.stack[self.top]
# 中缀表达式转后缀表达式
class InfixToPostfix:
def __init__(self, size):
# 1、初始化两个栈 s1, s2
self.s1 = ArrayStack(size)
self.s2 = ArrayStack(size)
def is_high_priority(self, oper1, oper2):
"""判断 oper1 的优先级是否大于 oper2,是返回 True"""
priority_dict = {
'+': 0,
'-': 0,
'*': 1,
'/': 1
}
prio1 = priority_dict.get(oper1)
prio2 = priority_dict.get(oper2)
if prio1 is None:
raise ValueError('不支持运算符' + oper1)
if prio2 is None:
raise ValueError('不支持运算符' + oper2)
return prio1 > prio2
def infix2postfix(self, infix_exp: str) -> list:
"""将中缀表达式转为后缀表达式返回"""
# 将中缀表达式字符串转换为列表
infix_list = self.str_to_list(infix_exp)
# 2、从左往右遍历中缀表达式,即遍历列表的每一个元素 ele
for ele in infix_list:
# 3、遇到的元素 ele 是数字,直接压入栈 s2
if '0' <= ele <= '9':
self.s2.push(ele)
# 4、遇到的元素 ele 是运算符,按以下三种情况处理:
elif ele != '(' and ele != ')':
while True:
# 4.1、如果栈 s1 为空,或者 s1 栈顶为左括号 ( ,则直接将元素 ele 压入栈 s1
if self.s1.is_empty() or self.s1.get_top() == '(':
self.s1.push(ele)
break
# 4.2、如果不满足4.1,则比较元素 ele 和 s1 栈顶元素的优先级,
# 如果 ele 优先级大于 s1 栈顶元素,则直接将元素 ele 压入栈 s1
elif self.is_high_priority(ele, self.s1.get_top()):
self.s1.push(ele)
break
# 4.3、如果不满足4.1、4.2,则弹出 s1 栈顶元素压入 s2,
# 然后回到 4.1 步重新判断元素 ele 和 s1 栈顶元素的关系
else:
self.s2.push(self.s1.pop())
# 5、遇到的元素 ele 是左括号 ( ,直接压入栈 s1
elif ele == '(':
self.s1.push(ele)
# 6、遇到的元素 ele 是右括号 ) ,依次弹出 s1 元素,并将弹出的元素压入 s2,
# 直到弹出的元素是 左括号 ( ,则停止弹出 s1 元素,并且将弹出的左括号丢弃,不压入栈 s2
else:
val = self.s1.pop()
while val != '(':
self.s2.push(val)
val = self.s1.pop()
# 7、重复步骤2-6,直到列表遍历完毕,将栈 s1 剩余的元素依次弹出压入栈 s2 ,
# 此时栈 s2 中的元素,从栈底到栈顶的顺序就是得到的后缀表达式
while not self.s1.is_empty():
self.s2.push(self.s1.pop())
result = []
# 依次弹出 s2 栈顶元素,并添加到列表 result 中
while not self.s2.is_empty():
result.append(self.s2.pop())
# 将列表 result 反转,得到的才是后缀表达式
result.reverse()
return result
def str_to_list(self, infix_expression: str) -> list:
"""将中缀表达式字符串转换为列表"""
# 将字符串转换为列表,并去除字符串中的空格
infix_list = [i for i in infix_expression if i != ' ']
# 遍历列表,将多位数合并成一个字符串
i = 0
while i < len(infix_list):
val = infix_list[i]
# 如果该元素是数字
if '0' <= val <= '9':
next = infix_list[i + 1] if i + 1 < len(infix_list) else None
# 判断列表的下一个元素是不是数字,是的话说明是多位数,需要进行拼接
while next and '0' <= next <= '9':
val += next # 拼接数字
infix_list.pop(i + 1) # 并从列表中移除下一位数字
# 继续判断下一个元素是不是数字,如果是还需要继续拼接
next = infix_list[i + 1] if i + 1 < len(infix_list) else None
# 将拼接好的多位数赋值给i,即列表中遇到的多位数的第一个数字的位置
infix_list[i] = val
i += 1
return infix_list # 返回转换后的中缀表达式列表
# 1+((2+3)* 4)-5 转为后缀表达式: 1 2 3 + 4 * + 5 -
s = '1+((2+3)* 4)-5'
infix_to_postfix = InfixToPostfix(len(s))
print(infix_to_postfix.infix2postfix(s)) # 1 2 3 + 4 * + 5 -