多元线性回归：

# coding=utf-8
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

if __name__ == '__main__':
    X1 =[12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
        2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8,
         29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
        11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59]
    X2 =[29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
        11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59,
         12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
         2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8]
    Y= []
    for i in range(len(X1)):
        Y.append(2 * X1[i] +3*X2[i]+ 5)
    # for i in range(1):
    X1.append(4.5)
    X1.append(15)
    X2.append(10)
    X2.append(20)
    Y.append(100)
    Y.append(10)
    #特征缩放
    X1_train=[]
    X2_train=[]
    for i in range(len(X1)):
        X1_train.append(X1[i]/(max(X1)-min(X1)))
        X2_train.append(X2[i] / (max(X2) - min(X2)))
    w1=1
    w2=-1
    b=2
    a=0.001 # 学习率
    lda=1 #正则化参数
    w1_temp=-100
    w2_temp = -100
    b_temp=-100
    w1change = 100
    w2change = 100
    bchange = 100
    while abs(w1change)>1e-12 and abs(w2change)>1e-12 and abs(bchange)>1e-12:
        print(w1change)
        w1change=0
        w2change=0
        bchange=0
        for i in range(len(X1)):
            w1change+=(w1*X1[i]+w2*X2[i]+b-Y[i])*X1[i]+lda*w1
            w2change += (w1 * X1[i] + w2 * X2[i] + b - Y[i]) * X2[i]+lda*w2
            bchange+=w1*X1[i]+ w2 * X2[i]+b-Y[i]
        w1change/=len(X1)
        w2change /= len(X2)
        bchange /= len(X1)
        w1_temp=w1-a*w1change
        w2_temp = w2 - a * w2change
        b_temp=b-a*bchange
        w1=w1_temp
        w2 = w2_temp
        b=b_temp
    print("y=%.4f*x1+%.4f*x2+%.4f" % (w1,w2, b))

  # 创建网格点
    x = np.linspace(0, 50, 100)
    y = np.linspace(0, 50, 100)
    X_point, Y_point = np.meshgrid(x, y)

  # 计算对应的Z值
    Z =w1*X_point+w2*Y_point+b

  # 创建三维图形
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')

  # 绘制二元函数曲面
    ax.plot_surface(X_point, Y_point, Z, cmap='viridis')

   # 绘制点
    points = []
    for i in range(len(X1)):
        points.append((X1[i],X2[i],Y[i]))
    for point in points:
       ax.scatter(point[0], point[1], point[2], color='red')

   # 添加标签和标题
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title('3D Plot')

# 显示图形
    plt.show()

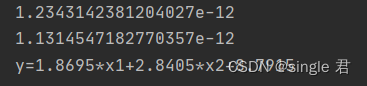
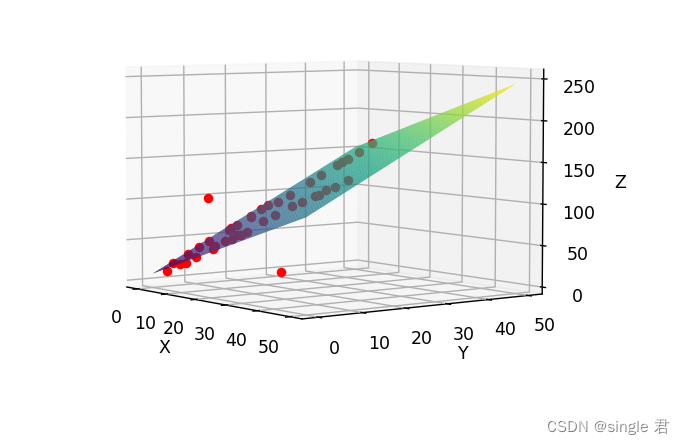
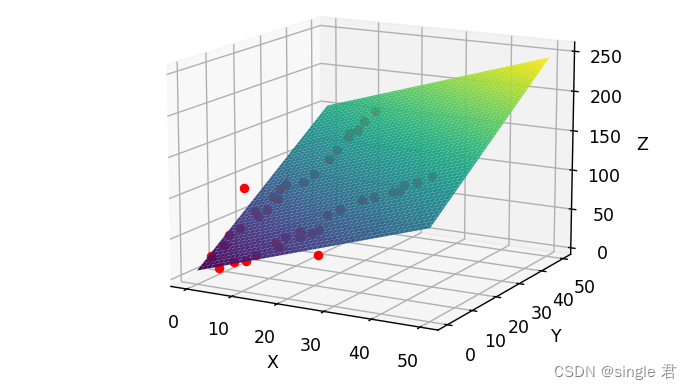
效果还不错。

逻辑回归中加入噪声：

# coding=utf-8
import matplotlib.pyplot as plt
import numpy as np

def f(w1,x1,w2,x2,b):
    z=w1*x1+w2*x2+b
    return 1/(1+np.exp(-z))
if __name__ == '__main__':
    X1 =[12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
        2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8,
         29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
        11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59]
    X2 =[29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
        11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59,
         12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
         2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8]
    Y= []
    for i in range(len(X1)):
        if X1[i]+X2[i]<20:Y.append(0)
        else:Y.append(1);

    #制造噪声
    for i in range(2):
        if Y[3*i+1]==1:Y[3*i+1]=0
        else:Y[3*i+1]=1
    w1=1
    w2=-1
    b=2
    a=5 # 学习率
    lda=0.01 #正则化参数
    w1_temp=-100
    w2_temp = -100
    b_temp=-100
    w1change = 100
    w2change = 100
    bchange = 100
    while abs(w1change)>1e-6 and abs(w2change)>1e-6 and abs(bchange)>1e-6:
        print(w1change)
        w1change=0
        w2change=0
        bchange=0
        for i in range(len(X1)):
            w1change+=(f(w1,X1[i],w2,X2[i],b)-Y[i])*X1[i]+lda*w1
            w2change += (f(w1,X1[i],w2,X2[i],b) - Y[i]) * X2[i]+lda*w2
            bchange+=(f(w1,X1[i],w2,X2[i],b) - Y[i])
        w1change/=len(X1)
        w2change /= len(X2)
        bchange /= len(X1)
        w1_temp=w1-a*w1change
        w2_temp = w2 - a * w2change
        b_temp=b-a*bchange
        w1=w1_temp
        w2 = w2_temp
        b=b_temp
    print("y=%.4f*x1+%.4f*x2+%.4f" % (w1,w2, b))
    print(Y)


    X1_1 = []
    X1_2 = []
    X2_1 = []
    X2_2 = []
    for i in range(len(X1)):
        if(Y[i]==0):
            X1_1.append(X1[i])
            X2_1.append(X2[i])
        else:
            X1_2.append(X1[i])
            X2_2.append(X2[i])
    print(X1_1)
    # 简单画图显示
    plt.scatter(X1_1, X2_1, c="blue")
    plt.scatter(X1_2, X2_2, c="red")

    x = np.linspace(0, 40, 200)  # 在0到50之间生成100个等间距的值
    y=(w1*x+b)/(-w2)
    plt.plot(x,y)

    plt.show()

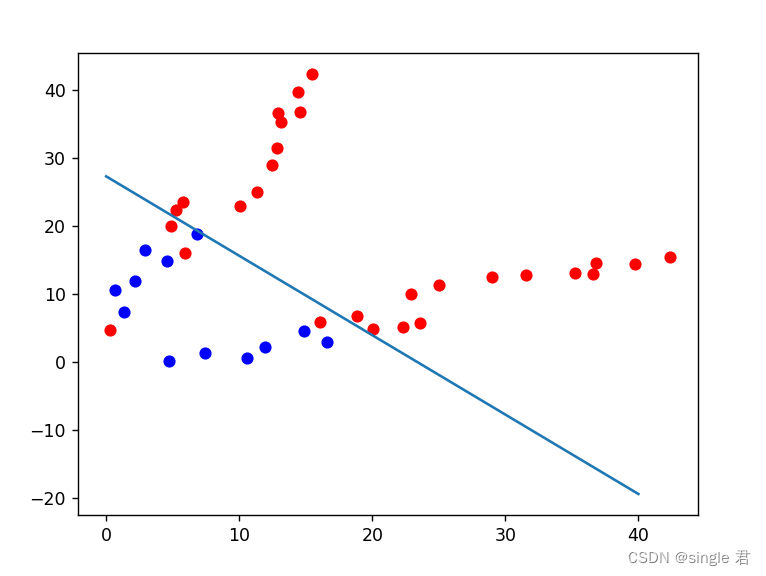
额，想用多项式优化一下逻辑回归结果跑不出来，很离谱。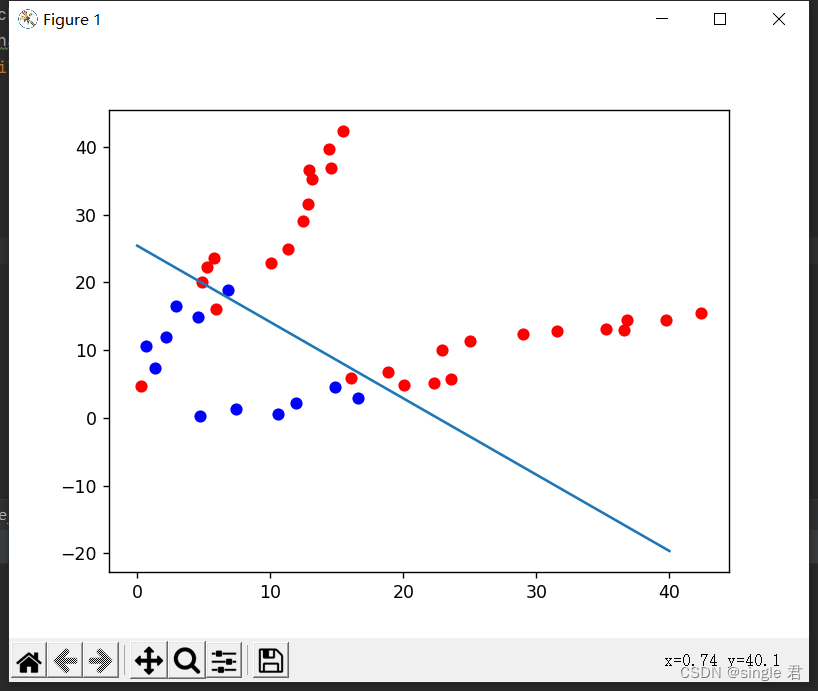
如果不正则化的话，对训练集的拟合效果会更好一些。