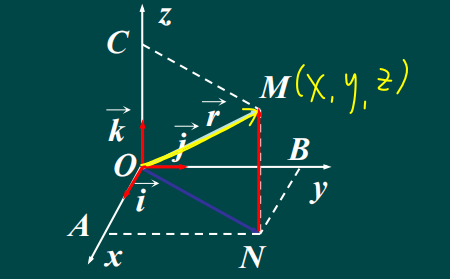
空间中的曲线与曲面
知识点1 曲面方程定义
定义1 如果曲面 S 与方程F (x,y,z ) = 0 有下述关系:
(1) 曲面 S 上的任意点的坐标都满足此方程
(2)不在曲面S上的点的坐标不满足此方程
则F(x,y,z)= 0 叫做曲面S的方程,曲面S叫做方程F (x,y,z) = 0 图形。
注 F(x,y,z)⛵️ 三元方程
两个基本应用问题
(1) 已知一曲面作为点的几何轨迹时,研究其点的坐标满足的代数式;
(2)已知方程式,研究他所表示的几何形状。

曲面方程定义–球面
-
求动点到定点M(x0,y0,z0)距离为R的轨迹方程。
解:设轨迹上动点为M1(x,y,z),依题意|MM1| = R
( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R \sqrt{(x-x0)^2 + (y-y0)^2 + (z - z0)^2 }= R (x−x0)2+(y−y0)2+(z−z0)2=R
故所求方程为:
( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 (x-x0)^2 + (y-y0)^2 + (z - z0)^2 = R^2 (x−x0)2+(y−y0)2+(z−z0)2=R2
特别地,当M0在原点时,球面方程为
x 2 + y 2 + z 2 = R 2 x^2+y^2+z^2=R^2 x2+y2+z2=R2
z = ± R 2 − x 2 − y 2 z = \pm \sqrt{R^2-x^2-y^2} z=±R2−x2−y2 表示上(下)半球面

标准式:
A x 2 + B y 2 + C z 2 − D x + E y + F = 0 Ax^2 + By^2 + Cz^2- Dx + Ey + F = 0 Ax2+By2+Cz2−Dx+Ey+F=0
一般式:
( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 (x-x0)^2 + (y-y0)^2 + (z-z0)^2 = R^2 (x−x0)2+(y−y0)2+(z−z0)2=R2
球心(x0,y0,z0)
半径 R
没有球心,和半径公式
曲面关于坐标面的对称性
定理1: 设曲面S 的方程F(x,y,z)= 0 ,则曲面S关于oxy平面对称的充要条件是,如果点P(x,y,z)的坐标满足方程F(x,y,z)= 0 ,那么必有点 P ‘ P^` P‘(x,y,-z)的坐标也满足方程F(x,y,-z) =0.
简言之,曲面S关于Oxy平面对称的充要条件是F(x,y,z)= F(x,y,-z).
同理可得,曲面S关于Oyx平面对称的充要条件是 F(-x,y,z) = F(x,y,z)。
曲面S关于Ozx平面对称的充要条件是 F(x,-y,z)= F(x,y,z)。
曲面方程–旋转曲面
一条平面曲线绕其平面上一条定直线旋转一周所形成的曲面叫做选装曲面。该定直线称为旋转轴。该曲线称为母线。

只讨论母线在坐标面上,且以坐标轴为旋转轴的旋转面的旋转面方程曲面。
如:oxy平面上的曲线 C:F(y,z) = 0 绕z轴旋转所生成的旋转面方程F( ± x 2 + y 2 , z \pm \sqrt{x^2+y^2},z ±x2+y2,z)= 0
如:oyz平面上的曲线C:F(y,z) = 0 绕z轴旋转所生成的旋转面方程F($y,\sqrt{x2+z2} = 0 $)
例5 求 Oyz 平面上的直线 z = a y ( a > 0 ) z = ay(a > 0) z=ay(a>0)绕 z 轴旋转所生成的旋
转面方程。
解:由分析可知,绕 z 轴转,即 z 不变, y 变成 ± x 2 + y 2 \pm \sqrt{x^2+y^2} ±x2+y2,
故而可得: z = ± x 2 + y 2 z = \pm \sqrt{x^2+y^2} z=±x2+y2
整理可得: z 2 = a 2 ( x 2 + y 2 ) z^2 = a^2(x^2+y^2) z2=a2(x2+y2)
这是顶点在原点的圆锥面。
例6 将以上的母线变成抛物线 z = a y 2 ( a > 0 ) z = ay^2(a>0) z=ay2(a>0)
可得旋转抛物面 z = a ( x 2 + y 2 ) z = a(x^2 + y^2) z=a(x2+y2)
曲面方程–柱面方程
定义2 平行定直线 L 并沿定曲线 C 移动的直线 L 形成的轨迹叫做柱
面。C 叫做准线, L 叫做母线。
-
常见柱面举例
y 2 = 2 x 表示抛物柱面; y^2 = 2x 表示抛物柱面; y2=2x表示抛物柱面;
x 2 + y 2 = R 2 表示圆柱面; x^2 + y^2 = R^2表示圆柱面; x2+y2=R2表示圆柱面;
x 2 a 2 + y 2 b 2 = 1 表示椭圆柱面; \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 表示椭圆柱面; a2x2+b2y2=1表示椭圆柱面;
x 2 a 2 − y 2 b 2 = 1 表示双曲柱面; \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 表示双曲柱面 ; a2x2−b2y2=1表示双曲柱面;
x − y = 0 表示平面; x-y=0 表示平面; x−y=0表示平面;

柱面分类:
(1) 方程F(x , y)=0 表示柱面,母线平行与z轴;准线 oxy面上的曲线L1;
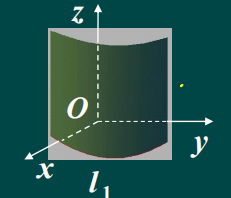
(2)方程G(y,z)= 0 表示柱面,母线平行与x轴;准线 oyz面上的曲线L2;
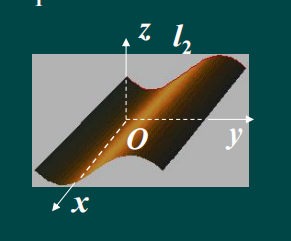
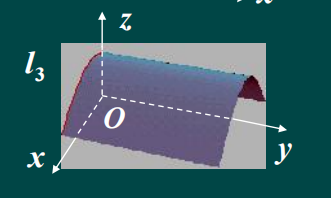
(3)方程H(z,x) = 0 表示柱面,母线平行与y轴;准线oxz面上的曲线L3;
空间曲线的参数方程
1.一般式方程定义
定义3 空间曲线可视为两曲面的交线,其一般方程为方程组:
{
F
(
x
,
y
,
z
)
=
0
G
(
x
,
y
,
z
)
=
0
\left\{ \begin{array}{c} F(x,y,z) = 0 \\ G(x,y,z) = 0 \\ \end{array} \right.
{F(x,y,z)=0G(x,y,z)=0

例如,方程组:
{
x
2
+
y
2
=
1
2
x
+
3
z
=
6
\left\{ \begin{array}{c} x^2 + y^2 = 1 \\ 2x + 3z = 6 \\ \end{array} \right.
{x2+y2=12x+3z=6

表示圆柱面与平面的交线 C 。
2.参数式方程定义
定义4 将曲线 C 上的动点坐标x,y,z 表示成参数 t 的函数,
随着 t 的变动,可得 C 上全部的点。
$$
\left{
\begin{array}{c}
x = x(t) \
y = y(t) \
z = z(t) \
\end{array}
\right.
称它为空间曲线的参数方程。
$$
的动点坐标x,y,z 表示成参数 t 的函数,
随着 t 的变动,可得 C 上全部的点。
{
x
=
x
(
t
)
y
=
y
(
t
)
z
=
z
(
t
)
称它为空间曲线的参数方程。
\left\{ \begin{array}{c} x = x(t) \\ y = y(t) \\ z = z(t) \end{array} \right. 称它为空间曲线的参数方程。
⎩
⎨
⎧x=x(t)y=y(t)z=z(t)称它为空间曲线的参数方程。