这两天为了一个小汇报搞得突击。
由于认真突击了n小时，所以上课听得也认真。外加这老师讲得蛮清楚的，所以整理个笔记。

---

图像三维重建的思路：

图源： https://zhuanlan.zhihu.com/p/34160526

由三维形成图片

单目、双目或者多目视觉测量

小孔成像原理

由图像还原三维

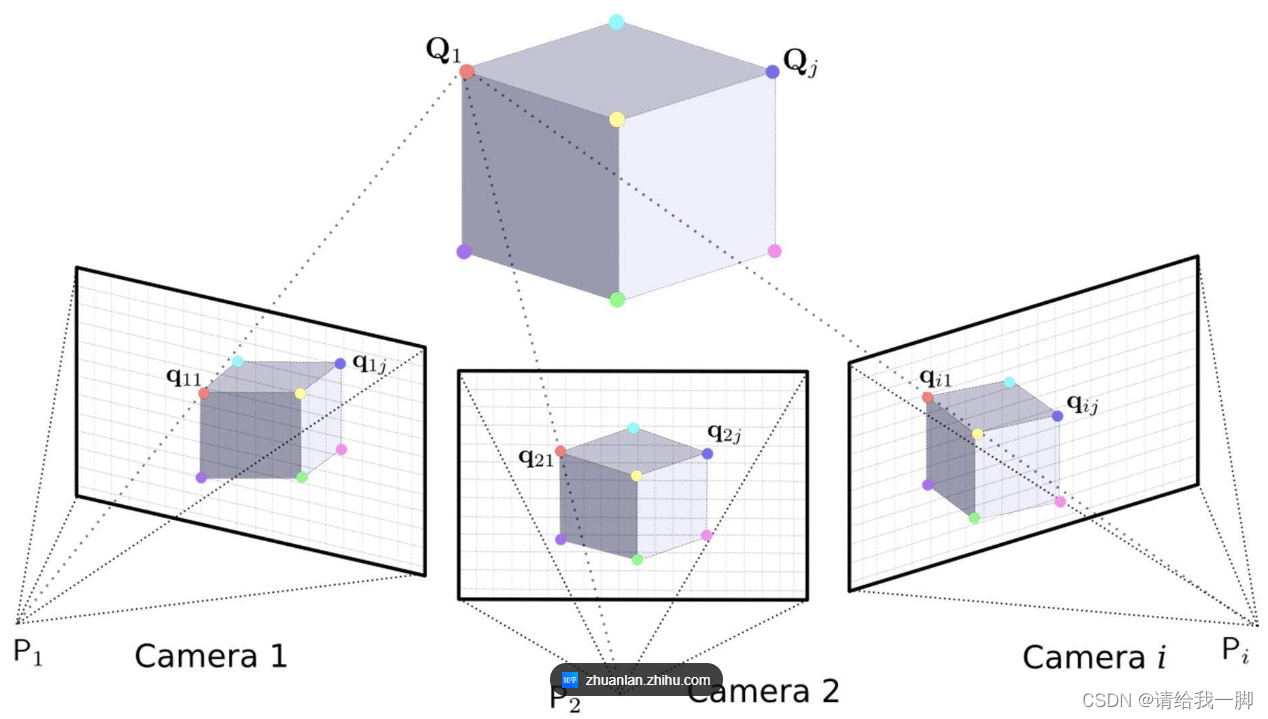
看上面的图，已知三幅图像上的点坐标q11，q21和qi1，他们和原物体点的连线Q1
只需要求得三条连线的方程就能解出点Q的坐标。
而求线的方程，只需要知道点坐标q，以及连线的法向量。

因此，怎么重建捏

先空三，求解相机的内外方位元素，外方位元素对应相机的位置和姿态，内方位元素对应相机的焦距和一些固有属性
在这一步中包含了，特征匹配步骤

然后再利用求得的内外方位元素，以及控制点坐标，进行前方交会，获得绝对的三维坐标。

归根到底，还是上面那个图

SfM(Structure from Model)

一种稀疏点云的建立方法。主要在开源软件中用得多，比如colmap，openmvg，openmvs等

那么SfM是啥捏。

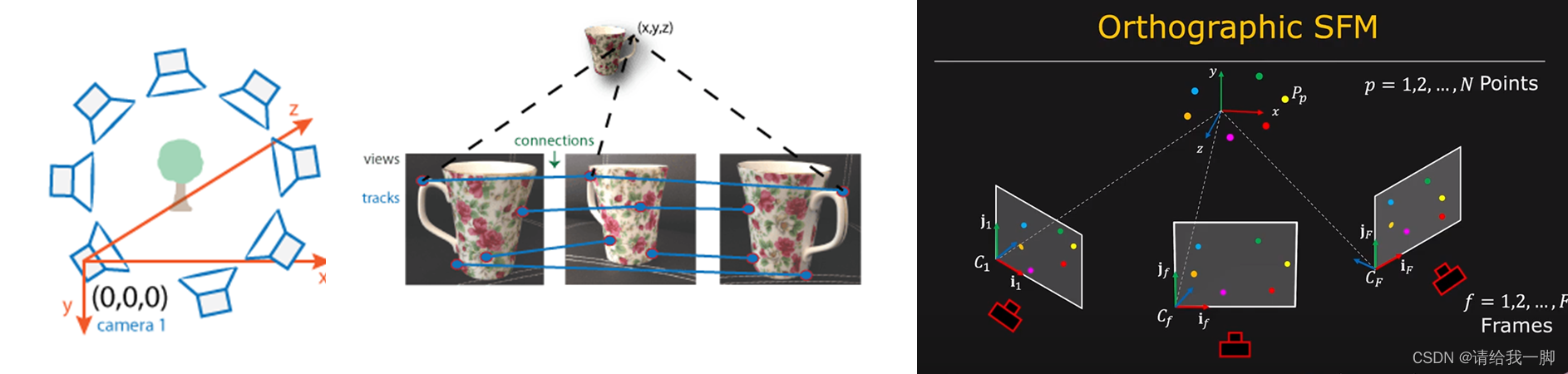
https://www.mathworks.com/help/vision/ug/structure-from-motion.html
图3截取自油管视频，，搜索SfM就有，一个系列

假设相机1位于原点，也就是图所示。z轴方向为光轴方向。
先使用相机1和相机2拍的图像1和图像2，如中间图，利用一些特征匹配技术进行匹配，求解相机的位姿，也就是求解空三
然后根据得到的矩阵参数，计算相机1和相机2之间的位姿。

下一步，又去判断相机2和相机3的位姿，相机4和相机3的位姿，依次计算，最终获得一个整体的位姿关系和特征匹配点，而所依照的坐标系，是一开始相机1的坐标系。

这样一个相机一个相机依次添加，叫，增量式SfM
而一次性把所有相机都添加进行求解，叫，全局式SfM

注意，SfM，生成的只是稀疏点云

现在再回到这个流程图。
面片就是生成的不规则三角网TIN组成的白膜。好处有三：一是稳定三角形，二是可以表示多样化的形状，三是可以计算表面积

另外，流程中 存在着配准误差，校准误差等，累积形成漂移，需要处理

激光三维重建

这个目前也有。但我了解不多。