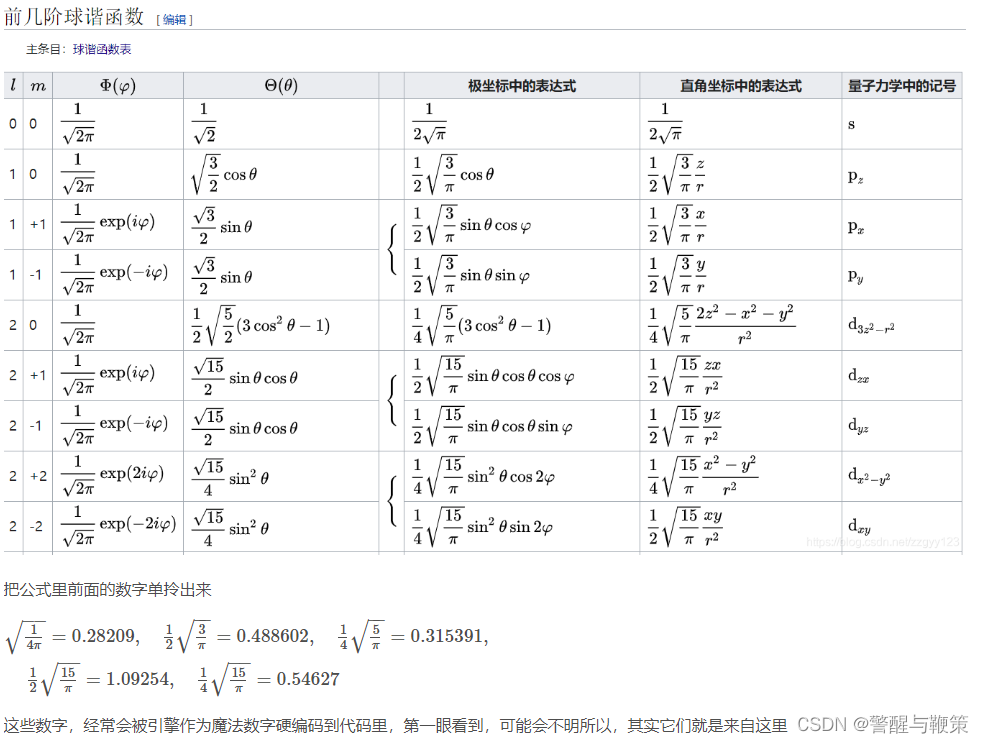
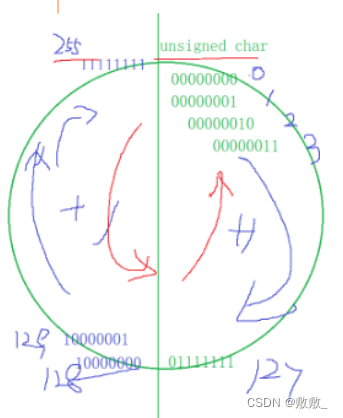
在三维空间中如何对场景光照进行球谐函数展开
图形学论文解析与复现【Spherical Harmonic Lighting:The Gritty Details】
首先,对场景中某像素点的漫反射光照进行计算。
L
(
p
,
w
o
)
=
∫
Ω
L
(
w
i
)
n
⋅
w
i
d
w
i
L(p,w_o) = \int_{\Omega}L(w_i)n\cdot w_idw_i
L(p,wo)=∫ΩL(wi)n⋅widwi
设:
L
i
=
∑
i
=
0
L
i
Y
i
(
ω
)
n
⋅
ω
=
t
(
ω
)
=
∑
i
=
0
t
i
Y
i
(
ω
)
L_i = \sum_{i=0}L_iY_i(\omega)\\ \quad\\ n\cdot \omega = t(\omega) = \sum_{i=0}t_iY_i(\omega)
Li=i=0∑LiYi(ω)n⋅ω=t(ω)=i=0∑tiYi(ω)
将
L
(
p
,
w
o
)
L(p,w_o)
L(p,wo)球谐展开后得到
L
(
p
,
w
o
)
=
∑
i
=
0
n
2
L
(
w
i
)
n
⋅
w
i
L(p,w_o) = \sum_{i=0}^{n^2}L(w_i)n\cdot w_i
L(p,wo)=i=0∑n2L(wi)n⋅wi
漫反射环境光
计算 L i L_i Li项
L i = ∑ i = 0 n 2 L ( w i ) Y i ( w ) L_i = \sum_{i=0}^{n^2} L(w_i)Y_i(w) Li=i=0∑n2L(wi)Yi(w)
for(pixel &p : Cubemap)
Li += p.color * Yi(normalise(p.position)) * dw;
计算 t i t_i ti项
t
i
=
∑
i
=
0
n
2
n
⋅
w
Y
i
(
w
)
d
w
t_i = \sum_{i=0}^{n^2} n\cdot w Y_i(w)dw
ti=i=0∑n2n⋅wYi(w)dw
可惜求
t
i
t_i
ti是与具体着色点有关(需要知道法线信息n)。这也就意味着,我们如果需要预计算
t
i
t_i
ti,也就需要对每一个方向的法线n 都要算一组
t
i
t_i
ti。每个像素点需要生成
i
i
i个(球谐基函数个)系数。
for(normal &n: sphere)//对于每个法线方向
{
for(pixel &p : Cubemap)//对Cubemap进行采样积分
Ti[n] += dot(n,normalise(p.position)) * Yi(normalise(p.position)) * dw;
}
但这样不就没有解决IBL需要对像素采样,导致移动端速度下降的问题了吗!!!!
我们引入不需要预计算 t i t_i ti的方式
辐照度环境贴图的有效表示
【论文复现】An Efficient Representation for Irradiance Environment Maps
采用球谐函数旋转特性解决每一个法线都需要预计算球谐函数的问题
如果我们已知
Y
l
m
(
u
)
Y_l^m(\mathbf{u})
Ylm(u) 是
u
\mathbf u
u 方向下的球谐函数项的计算结果。
那么如果我们想要知道
v
\mathbf v
v 方向下的球谐函数项的计算结果,就需要再计算一次。
但如果我们可以得到
u
\mathbf u
u到
v
\mathbf v
v下的矩阵
R
α
,
β
,
γ
(
u
)
R^{\alpha,\beta,\gamma}(\mathbf{u})
Rα,β,γ(u)
则可以得到
Y
l
m
(
R
α
,
β
,
γ
(
u
)
)
=
∑
m
′
=
−
l
l
D
m
′
,
m
l
(
R
α
,
β
,
γ
)
Y
l
m
′
(
u
)
D
m
′
,
m
l
(
R
α
,
β
,
γ
)
=
e
−
i
m
′
α
d
m
′
,
m
l
(
β
)
e
−
i
m
γ
\begin{array}{c} Y_{l}^{m}\left(R^{\alpha, \beta, \gamma}(\mathbf{u})\right)=\sum_{m^{\prime}=-l}^{l} D_{m^{\prime}, m}^{l}\left(R^{\alpha, \beta, \gamma}\right) Y_{l}^{m^{\prime}}(\mathbf{u}) \\ D_{m^{\prime}, m}^{l}\left(R^{\alpha, \beta, \gamma}\right)=e^{-i m^{\prime} \alpha} d_{m^{\prime}, m}^{l}(\beta) e^{-i m \gamma} \end{array}
Ylm(Rα,β,γ(u))=∑m′=−llDm′,ml(Rα,β,γ)Ylm′(u)Dm′,ml(Rα,β,γ)=e−im′αdm′,ml(β)e−imγ
其中 d m ′ , m l d^l_{m',m} dm′,ml 为维格纳D矩阵。
将上式代入球谐函数
f
(
u
)
=
∑
l
∞
c
l
m
Y
l
m
(
u
)
f(u) = \sum_l^\infin{c_l^mY_l^m(u)}
f(u)=l∑∞clmYlm(u)
得到
f
(
R
α
,
β
,
γ
(
u
)
)
=
∑
l
∞
∑
m
=
−
l
l
c
l
m
Y
l
m
(
R
α
,
β
,
γ
(
u
)
)
=
∑
l
∞
∑
m
′
=
−
l
l
g
l
m
′
Y
l
m
′
(
u
)
g
l
m
′
=
∑
m
=
−
l
l
c
l
m
D
m
′
,
m
l
(
R
α
,
β
,
γ
)
\begin{array}{c} f\left(R^{\alpha, \beta, \gamma}(\mathbf{u})\right)=\sum_{l}^{\infty} \sum_{m=-l}^{l} c_{l}^{m} Y_{l}^{m}\left(R^{\alpha, \beta, \gamma}(\mathbf{u})\right) =\sum_{l}^{\infty} \sum_{m^{\prime}=-l}^{l} g_{l}^{m^{\prime}} Y_{l}^{m^{\prime}}(\mathbf{u}) \\ \quad\\ g_{l}^{m^{\prime}}=\sum_{m=-l}^{l} c_{l}^{m} D_{m^{\prime}, m}^{l}\left(R^{\alpha, \beta, \gamma}\right) \end{array}
f(Rα,β,γ(u))=∑l∞∑m=−llclmYlm(Rα,β,γ(u))=∑l∞∑m′=−llglm′Ylm′(u)glm′=∑m=−llclmDm′,ml(Rα,β,γ)
根据上式,我们可以得出,如果要计算一个旋转之后的球谐函数,只需要对原来球谐函数的球谐系数处理就好。
处理方程即是:
g
l
m
′
=
∑
m
=
−
l
l
c
l
m
D
m
′
,
m
l
(
R
α
,
β
,
γ
)
g_{l}^{m^{\prime}}=\sum_{m=-l}^{l} c_{l}^{m} D_{m^{\prime}, m}^{l}\left(R^{\alpha, \beta, \gamma}\right)
glm′=m=−l∑lclmDm′,ml(Rα,β,γ)
漫反射环境光 L ( w i ′ ) L(w'_i) L(wi′)
- 只关心光线和法线的夹角,不考虑其他角度
- 只考虑m’=0的情况
得到
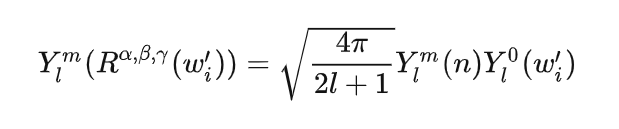
结合下式
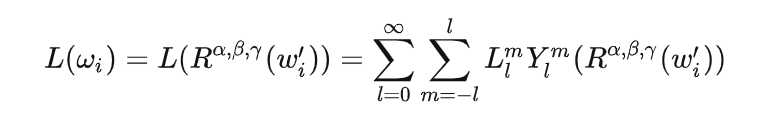
得到
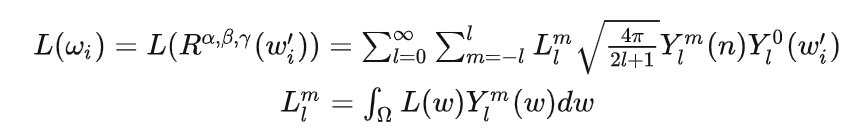
漫反射环境光 t ( θ ′ ) t(\theta') t(θ′)
最终结果
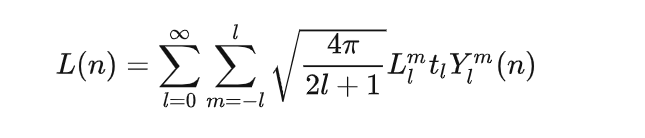
- 对于 L l m L_l^m Llm而言,仍需要预计算(与上一节相同)
- 对于
t
l
t_l
tl,与上一篇不同的是:已经变成了如下几个常数(只与l有关)与
Y
l
m
(
n
)
Y_l^m(n)
Ylm(n)的乘积
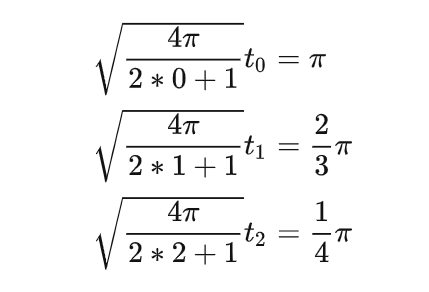
- 对于
Y
l
m
(
n
)
Y_l^m(n)
Ylm(n)项,他的参数是具体着色点的法线n。
该Y通过如下转换,得到法线n下的基坐标函数。再与外部预计算好的 L l m L_l^m Llm和 t l t_l tl进行简单乘积得到最终的漫反射环境光!
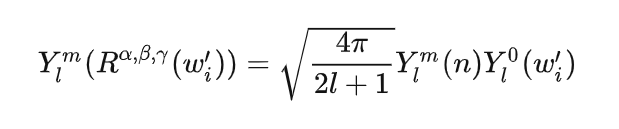
光泽(镜面)反射环境光
首先将光照方程列出
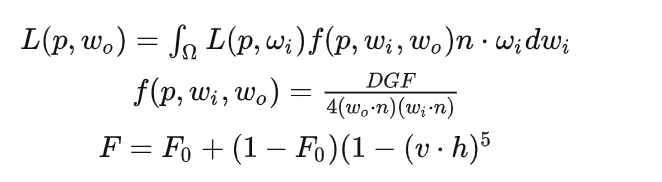
对光照方程进行分解
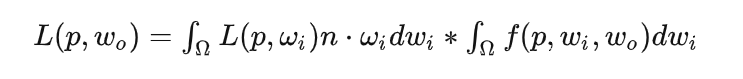
注意这里与IBL 文章中的分解方式不一样,
n
⋅
w
i
n\cdot w_i
n⋅wi被分到前面一部分了(IBL是分到后面一部分的)
但是球谐函数处理低频信息更好(意思是更适合处理漫反射或者是粗糙度比较大的光泽反射),因为对于纯镜面反射而言,我们需要非常高阶的球谐函数才能进行逼近,那计算量实在是太大了。
因此一般使用IBL处理高光环境光反射。
球谐函数也不是仅仅只能用于求环境光,这种将函数展开的思想还普遍用于解决顺序无关的透明度等问题。
参考