数据结构“栈”的一个用途就是:平衡符号,比如这样一个代数式:(a(b+c)*a(e*f+a*(c+d))),你能一眼看出这个式子的括号是否正确吗? 更何况还可以加入中括号([]),大括号({})。如果写一个算法来验证这个式子的话,利用栈这种数据结果是最方便的:
构造一个空栈,读入字符串直到文件尾。如果字符是一个开放符号,则将其推入栈中,如果字符是一个封闭符号,则房栈空时报错;否则将栈元素弹出。如果弹出的符号不是对应的开放符号,则报错。在文件尾,如果栈非空则报错。
检验括号是很简答的一个算法,这里就不是贴代码了。接下里想说的是数学计算式的计算,例如:“2+3*5“,给定这样一个简单的字符串能否得到正确的结果17,还是错误的结果25. 如果在加上括号()来改变运算优先级那么就更复杂了,例如计算“2+3*(4-3*3)+9”。
我们在数学作业上看见的计算式是顺序计算式,或者说叫中序计算式,我们人在计算时很容易处理这种式子,但是计算机并不好处理,因为在考虑“2+3*5”的时候,当计算机遍历字符到3时,并不能立马计算“2+3”,他必须考虑3后面的符号,也就是在这个过程中需要存储中间结果。
事实上,计算机处理这个问题时,更好的是处理后缀表达式(又叫逆波兰表达式,是一位波兰逻辑学家发明的),后缀表达式也很简单,举个例子“a+b*c”的后缀表达式为:"a b c* +", 那么后缀表达式是怎么计算的呢?
1.后缀表达式的计算
假设我们要计算的后缀表达式为:"6 5 2 3 + 8 + 3 +*",我们且看是如何计算的:
首先构造一个空栈S,我们遍历后缀表达式,将前4个数字依次入栈:得到下图中的a图:
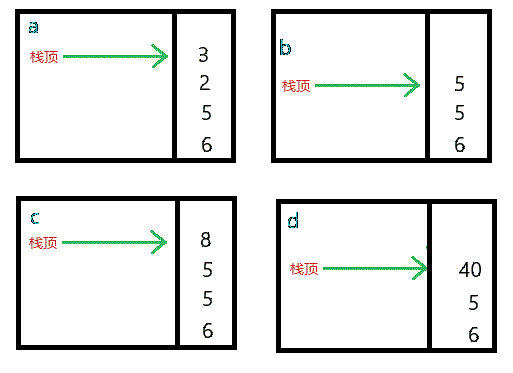
接下来是读入的是一个“+”,所以3和2依次弹出,并将他们的和5压入栈中得到图b,
接着数字“8”进栈,得到图c,然后是一个“*”运算符,同理弹出8和5,计算其结果后再重新入栈,得到图d,依次类推可以得到如下图结果:
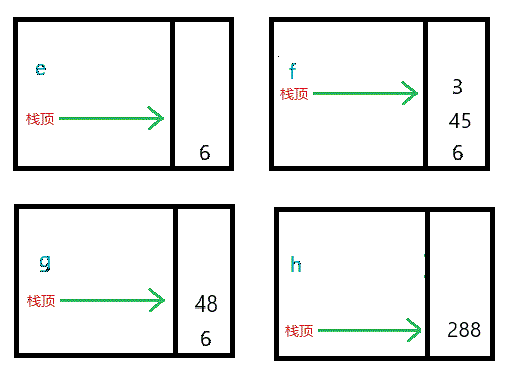
如果之前的括号平衡检测代码你没问题的话,那么这个计算后缀表达式的代码你肯定也没问题。
这里先贴一下计算的代码:
public static int GetValue(string postFix)
{
Stack<int> stack = new Stack<int>();
foreach (var c in postFix)
{
if (char.IsDigit(c))
{
stack.Push(c - '0');
}
else
{
var b=stack.Pop();
var a=stack.Pop();
var ans = Calculate(a, b, c);
stack.Push(ans);
}
}
return stack.Pop();
}Calculate是计算函数:
public static int Calculate(int a, int b, char op)
{
return op switch
{
'+' => a + b,
'-' => a - b,
'*' => a * b,
'/' => a / b,
_ => throw new ArgumentOutOfRangeException()
};
}为了简单起见,这里只考虑了10以内的加减乘除,若果大于10,则遍历的应该是字符串。其它的就没啥好说的了。
计算一个后缀表达式的时间是O(N),因为对输入中的每个元素的处理都是一些栈操作组成从而花费的常数时间。当我们得到一个后缀表达式之后,没有必要知道任何优先规则,这是一个明显的优点。那么问题来了,如何将一个自然表达式转为后缀表达式?
2.中缀表达式到后缀表达式的转换
假设我们有一个中缀表达式"a+b*c+(d*e+f)",要将其转化为后缀表达式:"a b c * + d e * f + g * +",
我们简单的分析一下:
首先后缀表达式的字母顺序和中缀表达式的字母顺序是一致的,这说明当我们遍历中缀时,如果用一个数组存储字母,那顺序是可以的。但是运算符的顺序缺发生了很多变化,仅看"a+b*c",加号+在前,但是转化为后缀表达式之后,+在*的后面,这说明遍历字符串时,符号的顺序不能用顺序结构存储。
我们在做题是,心理有一个默认的假设,那就是先乘除再加减,这其实就是运算符优先级,前面说道,计算机在对后缀表达式求值的时候,是不需要考虑运算符的优先级的,计算机每遇到一个运算符就立即计算。那这有什么启发呢?启发就是:我们在转换为后缀表达式的过程中利用了优先级,将优先级这一信息存储到后缀表达式中。
那再回到刚刚的"a+b*c",我们尝试构件一个栈用来存储运算符,首先+入栈,字母直接输出,遇到*,因为优先级高,故直接入栈,然后输出c,最后将符号依次出栈。
还是用图来解释:
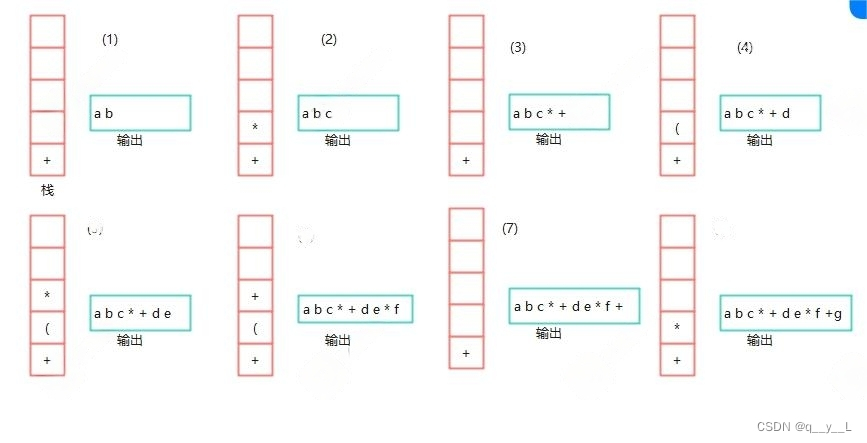
规则如下:
- 当读到一个操作数时,立即把它放到输出中。操作符不立即输出,所以必须先存在栈中。
- 如果遇见一个右括号,将右括号直接放入栈中
- 如果遇见左括号,将栈中的符号依次弹出,知道遇见右括号为止
- 如果是其它运算符号,那我们弹出栈元素直到发现优先级更低的元素为止。
- 最后,如果读到了文件末尾,将栈元素全部弹出。
上图第三步,遇到一个+,但是栈顶目前是*,因此要先弹出*,然后发现接着是+,优先级相同,也弹出,为空后,将刚刚的+入栈。但是括号要另外处理,只有括号才能弹出括号。代码如下:
public static string Change(string input)
{
Stack<char> op= new Stack<char>();
string result = "";
foreach(char c in input)
{
if(char.IsDigit(c))
{
result += c;
}
else if(c=='(')
{
op.Push(c);
}
else if(c== ')')
{
while(op.Peek()!='(')
{
result+=op.Pop();
}
op.Pop(); //弹出’C'
}
else
{
while(op.Count()>0)
{
var top=op.Peek();
if (Operations[top] <= Operations[c] && top!='(')
{
result+=op.Pop();
}
else
{
break;
}
}
op.Push(c);
}
}
while(op.Count() > 0)
{
result += op.Pop();
}
return result;
}其中会比较优先级;优先级我直接定义在一个静态字典:
public static readonly IDictionary<char, int> Operations = new Dictionary<char, int>()
{
['+'] = 10,
['-'] = 10,
['*'] = 5,
['/'] = 5,
['('] = 1, //特殊符号 特殊处理
[')'] = 2,
};到目前为止,我们就解决了前缀转后缀的问题,再结合之前的后缀计算方法,就可以得到最终结果。
事实上,如果运算符均是二元运算符,那么表达式还可以以树的形式展开。我们在后面会介绍如何将数学表达式转为表达式树。