Leetcode 易错题整理（三）73. 77. 78. 81. 90. 95.105. 130.

73. 矩阵置零

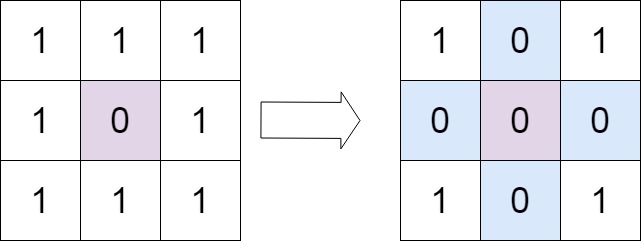
给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法**。**

示例 1：
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

笨方法：先遍历一次整个数组，获取到所有0位置，第二次把这里面所有0位置数字横竖都变为0.

原地算法：我们可以把这一行列是否有0的信息存到第一行和第一列，比如该数组第一次扫描完结果为：

1 0 1

0 0 1

1 1 1

上和左两个0表示这一行这一列后面应当被置零。第二次扫描的时候就只扫描第一行和第一列，把为0的行列头这一行列都置为0即可。

但是这样会出现一个问题，就是比如第一行第一列如果出现了0，那么第一行第一列也要被置为0. 但是我们无法判断这个0是本来就有的还是第一次遍历的时候数组中的元素传递过来的。

解决办法是我们再单独用两个变量存储第一行第一列是否存在0的信息，如果存在，那么最后再把第一行第一列置0.

class Solution {
    public void setZeroes(int[][] matrix) {
        boolean fstLineHas0=false;
        boolean fstColumnHas0=false;
        int xLen=matrix.length,yLen=matrix[0].length;
        for(int i=0;i<xLen;i++){
            if(matrix[i][0]==0){
                fstColumnHas0=true;
                break;
            }
        }
        for(int j=0;j<yLen;j++){
            if(matrix[0][j]==0){
                fstLineHas0=true;
                break;
            }
        }
        for(int i=1;i<xLen;i++){
            for(int j=1;j<yLen;j++){
                if(matrix[i][j]==0){
                    matrix[i][0]=0;
                    matrix[0][j]=0;
                }
            }
        }
        for(int i=1;i<xLen;i++){
            if(matrix[i][0]==0){
                for(int j=1;j<yLen;j++)matrix[i][j]=0;
            }
        }
        for(int j=1;j<yLen;j++){
            if(matrix[0][j]==0){
                for(int i=1;i<xLen;i++)matrix[i][j]=0;
            }
        }
        if(fstColumnHas0)for(int i=0;i<xLen;i++)matrix[i][0]=0;
        if(fstLineHas0)for(int j=0;j<yLen;j++)matrix[0][j]=0;
    }
}

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：
输入：n = 1, k = 1
输出：[[1]]

一开始我就是写了一个简单的递归遍历，自然是超时了。

public void dfs(List<List<Integer>> resList, int n, int k){
        
        if(k==0)return;
        if(resList.size()==0){
           for(int i=1;i<=n;i++){
               List<Integer> tempList=new ArrayList<>();
               tempList.add(i);
               resList.add(tempList);
           }
           dfs(resList,n,k-1);
        }
        else if(n<resList.get(0).size()+k){
            resList=new ArrayList<>();
            return;
        }
        else {
            int len=resList.size();
            List<Integer> fstList=resList.get(0);
            int max=fstList.get(fstList.size()-1);
            for(int i=0;i<len;i++){
                
                for(int j=max+1;j<=n;j++){
                    List<Integer> tempList=new ArrayList<>(resList.get(0));
                    tempList.add(j);
                    resList.add(tempList);
                }
                resList.remove(0);
            }
            dfs(resList,n,k-1);
        }
    }

后来看了官方题解，我没必要这样频繁地存取元素。

public void dfs1(List<List<Integer>> resList, List<Integer>tempList, int n, int k, int cur){
        
        if(tempList.size()==k){
            resList.add(new ArrayList<>(tempList));
            return;
        }
        else if(tempList.size()+(n-cur+1)<k){
            return;
        }
        else {
            tempList.add(cur);
            dfs1(resList,tempList,n,k,cur+1);
            tempList.remove(tempList.size()-1);
            dfs1(resList,tempList,n,k,cur+1);
        }
    }

只有一个 tempList 元素在不停地动态变化，我们只需要在其长度到达 k 时复制一份传入 resList 列表即可。

对于每次遍历的元素，我们选择是保留或忽略此元素，这样从所有元素都保留的结果到所有元素都忽略的结果都能考虑到。

这种算法叫做剪枝。当当前这个分支已经无法满足题意，或者已经可以判定非最优解了，就可以把这个枝剪掉，不要继续走了。

78. 子集

找出给定集合的所有子集（从空集到他自身都要找到）。

这个和上面的深度遍历是一个道理，区别在于“什么时候是一轮判断完成的标志”。上面一题是 tempList 长度到达 k 固定长度的时候结束并存入本轮循环的 list，此题可以是扫描完全数组时存入。

class Solution {
    List<List<Integer>> resList=new ArrayList<>();
    List<Integer> tempList=new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        dfs(0,nums);
        return resList;
    }

    public void dfs(int cur, int[] nums){
        if(cur==nums.length){
            resList.add(new ArrayList<>(tempList));
            return;
        }
        tempList.add(nums[cur]);
        dfs(cur+1,nums);
        tempList.remove(tempList.size()-1);
        dfs(cur+1,nums);
    }
}

81. 搜索旋转数组 II

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：
输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

主要可能出现的问题：形如 [1,1,1,1,3,1,1,1,1,1,1,1,1] 这样的数组，我们不确定特殊数处在什么位置。这样就不能用传统二分法一砍砍一半了。

class Solution {
    public boolean search(int[] nums, int target) {
        int left=0,right=nums.length-1;
        while(left<=right){
            int mid=(left+right)/2;
            if(nums[mid]==target)return true;
            else if(nums[left]==nums[mid]&&nums[right]==nums[mid]){//头尾缩减一点，来逐步排查特殊数部分
                left++;
                right--;
            }
            else if(nums[mid]<=nums[right]){
                if(nums[mid]<target&&nums[right]>=target)left=mid+1;//右侧自增，且 target 落在右侧区间中
                else right=mid-1;
                
            }
            else {
                if(nums[mid]>target&&nums[left]<=target)right=mid-1;//左侧自增，且 target 落在左侧区间中
                else left=mid+1;
            }
        }
        return false;
    }
}

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

和之前的组合总和题有些类似，主要是注意不要重复。

解法：统一规定，如果此次递归访问的元素和上一次一样，且上一次没有包含这个元素，那么本次递归不再尝试加入此元素。

class Solution {
    List<List<Integer>> resList=new ArrayList<>();
    List<Integer> tempList=new ArrayList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        dfs(nums, 0,false);
        return resList;
    }

    public void dfs(int[] nums, int cur,boolean visited){
        if(cur==nums.length){
            resList.add(new ArrayList<Integer>(tempList));
            return;
        }
        dfs(nums, cur+1,false);//可以放弃此元素继续递归
        if(cur>0&&nums[cur-1]==nums[cur]&&(!visited))return;//但是不能使用重复的元素，不然就和上一轮循环重复了。
        tempList.add(nums[cur]);
        dfs(nums, cur+1,true);
        tempList.remove(tempList.size()-1);
        
    }
}

95. 不同的二叉搜索树 II

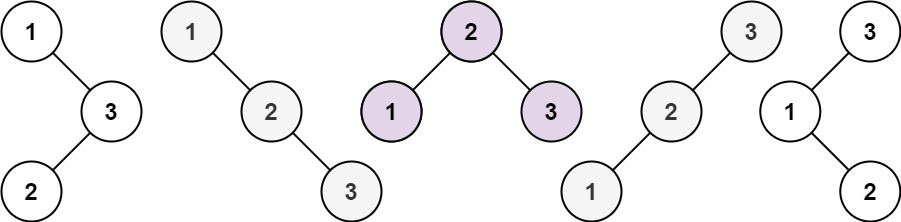
给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

还是有规律的。我们每次遍历选取一个节点作为根节点，左边的树递归生成左子树，右边递归生成右子树，两树再合并到根节点左右之下。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n==0)return new LinkedList<TreeNode>();
        return generateTree(1,n);
    }

    public List<TreeNode> generateTree(int start, int end){
        List<TreeNode> resList=new LinkedList<>();
        if(start>end){
            resList.add(null);
            return resList;
        };
        for(int i=start;i<=end;i++){
            List<TreeNode> leftTree=generateTree(start,i-1);
            List<TreeNode> rightTree=generateTree(i+1,end);
            for(TreeNode left:leftTree){
                for(TreeNode right:rightTree){
                    TreeNode root=new TreeNode(i);
                    root.left=left;
                    root.right=right;
                    resList.add(root);
                }
            }
        }
        return resList;
        
    }
}

105. 从前序与中序遍历序列构造二叉树

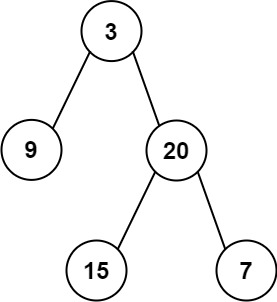
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

主要是一个思想。

preorder：形如 root, x, x, x, x..., x

inorder：形如 x, x, x, x... root, x, x... x

那么我们每次找到 root 和左子树右子树，递归继续操作即可。

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return f(preorder, inorder, 0,preorder.length-1,0,inorder.length-1);
    }

    public TreeNode f(int[] preorder, int[] inorder, int preLeft, int preRight, int inLeft, int inRight){
        if(preLeft>preRight)return null;
        TreeNode root=new TreeNode(preorder[preLeft]);
        int i=inLeft;
        while(inorder[i]!=preorder[preLeft])i++;
        root.left=f(preorder,inorder,preLeft+1,i-inLeft+preLeft,inLeft,i-1);
        root.right=f(preorder,inorder,preLeft+(i-inLeft)+1,preRight,i+1,inRight);
        return root;
    }
}

130. 被围绕的区域

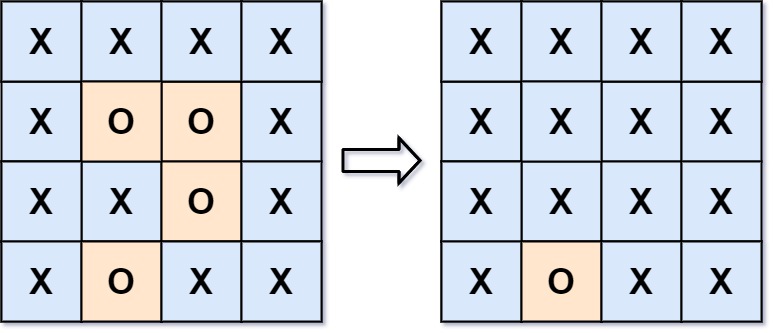
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

解决办法：首先我们扫描一下所有边界，对于其中值 =O 的元素，赋值=A 表示要保留，递归判断其上下左右中出现 O 的地方也作同样处理。

然后遍历整个数组，把 A 的部分改为 O，把 X O 都改成 X。

class Solution {
    public void solve(char[][] board) {
        int lineLen=board.length;
        int columnLen=board[0].length;
        for(int i=0;i<lineLen;i++){
            dfs(board,i,0);
            dfs(board,i,columnLen-1);
        }
        for(int i=0;i<columnLen;i++){
            dfs(board,0,i);
            dfs(board,lineLen-1,i);
        }
        for(int i=0;i<lineLen;i++){
            for(int j=0;j<columnLen;j++){
                if(board[i][j]=='A')board[i][j]='O';
                else board[i][j]='X';
            }
        }
    }

    public void dfs(char[][] board, int i, int j){
        if(i<0||i>=board.length)return;
        if(j<0||j>=board[0].length)return;
        if(board[i][j]=='A'||board[i][j]=='X')return;
        else board[i][j]='A';
        dfs(board,i,j-1);
        dfs(board,i,j+1);
        dfs(board,i-1,j);
        dfs(board,i+1,j);
    }
}