本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。

返回包含原始树中所有 最深节点 的 最小子树 。

如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。

一个节点的 子树 是该节点加上它的所有后代的集合。

示例 1：

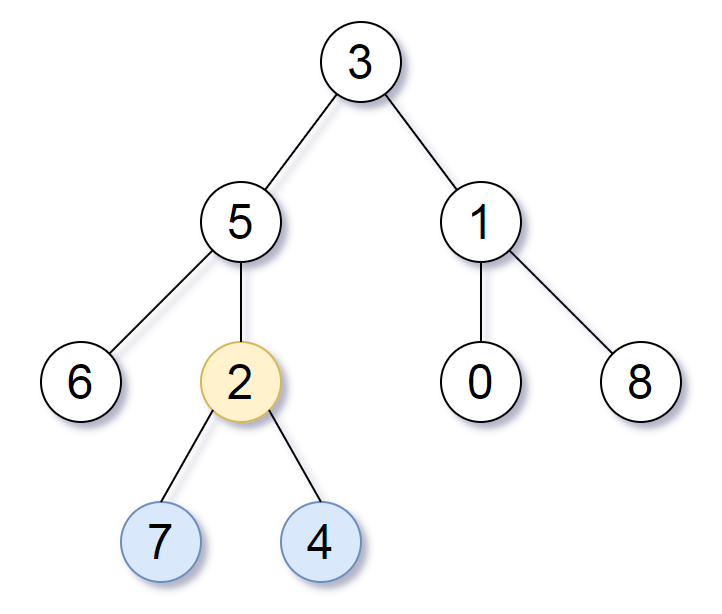
输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：
我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 5、3 和 2 包含树中最深的节点，但节点 2 的子树最小，因此我们返回它。

示例 2：

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点。

示例 3：

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的节点为 2 ，有效子树为节点 2、1 和 0 的子树，但节点 2 的子树最小。

提示：

• 树中节点的数量在 [1, 500] 范围内。
• 0 <= Node.val <= 500
• 每个节点的值都是 独一无二 的。

注意： 本题与力扣 1123 重复：https://leetcode-cn.com/problems/lowest-common-ancestor-of-deepest-leaves

---

解法1 递归

看上图（示例 1），这棵树的节点 $3,5,2$ 都是最深叶节点 $7,4$ 的公共祖先，但只有节点 $2$ 是最近的公共祖先。

如果我们要找的节点只在左子树中，那么最近公共祖先也必然只在左子树中。对于本题，如果左子树的最大深度比右子树的大，那么最深叶结点就只在左子树中，所以最近公共祖先也只在左子树中。反过来说，如果右子树的最大深度大于左子树，那么最深叶结点就只在右子树中，所以最近公共祖先也只在右子树中。

如果左右子树的最大深度一样呢？当前节点一定是最近公共祖先吗？不一定。比如节点 $1$ 的左右子树最深叶节点 $0,8$ 的深度都是 $2$ ，但该深度并不是全局最大深度，所以节点 $1$ 并不能是答案。

根据以上讨论，正确做法如下：

• 递归这棵二叉树，同时维护全局最大深度 $\text{maxDepth}$ 。
• 在「递」的时候往下传 $depth$ ，用来表示当前节点的深度。
• 在「归」的时候往上传当前子树最深叶节点的深度。
• 设左子树最深叶节点的深度为 $\text{leftMaxDepth}$ ，右子树最深叶节点的深度为 $\text{rightMaxDepth}$ 。如果 $\text{leftMaxDepth}=\text{rightMaxDepth}=\text{maxDepth}$ ，那么更新答案为当前节点。注意这并不代表我们找到了答案，如果后面发现了更深的叶节点，那么答案还会更新。

class Solution {
public:
    TreeNode *subtreeWithAllDeepest(TreeNode *root) {
        TreeNode *ans = nullptr;
        int max_depth = -1; // 全局最大深度
        function<int(TreeNode*, int)> dfs = [&](TreeNode *node, int depth) {
            if (node == nullptr) {
                max_depth = max(max_depth, depth); // 维护全局最大深度
                return depth;
            }
            int left_max_depth = dfs(node->left, depth + 1); // 获取左子树最深叶节点的深度
            int right_max_depth = dfs(node->right, depth + 1); // 获取右子树最深叶节点的深度
            if (left_max_depth == right_max_depth && left_max_depth == max_depth)
                ans = node;
            return max(left_max_depth, right_max_depth); // 当前子树最深叶节点的深度
        };
        dfs(root, 0);
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$\mathcal{O}(n)$ 。每个节点都会恰好访问一次。
• 空间复杂度：$\mathcal{O}(n)$ 。最坏情况下，二叉树是一条链，递归需要 O(n)\mathcal{O}(n)O(n) 的栈空间。

---

解法2 自底向上

也可以不用全局变量，而是把每棵子树都看成是一个「子问题」，即对于每棵子树，我们需要知道：

• 这棵子树最深叶结点的深度。这里是指叶子在这棵子树内的深度，而不是在整棵二叉树的视角下的深度。相当于这棵子树的高度。
• 这棵子树的最深叶结点的最近公共祖先 $\text{lca}$ 。

分类讨论：

• 设子树的根节点为 $node$，$node$ 的左子树的高度为 $\text{leftHeight}$ ，$node$ 的右子树的高度为 $\text{rightHeight}$ 。
• 如果 $leftHeight>rightHeight$ ，那么子树的高度为 $\text{leftHeight}+1$ ，$\text{lca}$ 是左子树的 $\text{lca}$ 。
• 如果 $\text{leftHeight}<\text{rightHeight}$ ，那么子树的高度为 $rightHeight+1$ ，$lca$ 是右子树的 $lca$ 。
• 如果 $\text{leftHeight}=\text{rightHeight}$ ，那么子树的高度为 $\text{leftHeight}+1$ ，$lca$ 就是 $node$ 。反证法：如果 $lca$ 在左子树中，那么 $lca$ 不是右子树的最深叶结点的祖先，这不对；如果 $lca$ 在右子树中，那么 $lca$ 不是左子树的最深叶结点的祖先，这也不对；如果 $lca$ 在 $node$ 的上面，那就不符合「最近」的要求。所以 $lca$ 只能是 $node$。

class Solution {
    pair<int, TreeNode*> dfs(TreeNode *node) {
        if (node == nullptr)
            return {0, nullptr};
        auto [left_height, left_lca] = dfs(node->left);
        auto [right_height, right_lca] = dfs(node->right);
        if (left_height > right_height) // 左子树更高
            return {left_height + 1, left_lca};
        if (left_height < right_height) // 右子树更高
            return {right_height + 1, right_lca};
        return {left_height + 1, node}; // 一样高
    }

public:
    TreeNode *subtreeWithAllDeepest(TreeNode *root) {
        return dfs(root).second;
    }
};

复杂度分析：

• 时间复杂度：$\mathcal{O}(n)$ 。每个节点都会恰好访问一次。
• 空间复杂度：$\mathcal{O}(n)$ 。最坏情况下，二叉树是一条链，递归需要 $\mathcal{O}(n)$ 的栈空间。

更简洁的写法是：

class Solution {
public:
    int depth[1010];
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        if (root == nullptr) return nullptr;
        TreeNode* left = root->left, *right = root->right;
        TreeNode* lcaLeft = subtreeWithAllDeepest(root->left), *lcaRight = subtreeWithAllDeepest(root->right);
        int dl = left ? depth[left->val] : 0, dr = right ? depth[right->val] : 0;
        depth[root->val] = max(dl, dr) + 1;
        if (dl > dr) return lcaLeft;
        if (dr > dl) return lcaRight;
        return root;
    }
};