方法一：加括号法示例

步骤： 
1、根据运算符的优先级对中缀表达式加括号（有几个运算符就有几对括号，原有的括号不用加）
2、将运算符移到对应括号后面
3、去掉所有括号，即为后缀表达式

以下面的中缀表达式为例：

9+(3-1)×3+8÷2

    1、变为（(9+((3-1)×3))+(8÷2)）
    2、变为（(9((3 1)-3)*)+(82)/）+
    3、得到9 3 1 - 3 * + 8 2 / +

解析：

①（3-1）=A作为一个整体；
②（（3-1）*3））=A*3=B作为一个整体；
③（9+（（3-1）*3））=（9+B）=C作为一个整体；
④（8/2）=D作为一个整体：
⑤（(9+((3-1)×3))+(8÷2)）=（C+D）作为一个整体：

最后再逆序求后缀表达式：
⑤ 改为C D-  ，C和D都认为是两个数  ，也就是 (9+((3-1)×3))  (8÷2)  -
④ 将 (9+((3-1)×3)) 继续改为 

最后输出后缀表达式为：

    9 3 1 - 3 * + 8 2 / +

方法二：栈的应用-四则运算表达式求值

2.1.1 栈的应用-四则运算表达式求值规则

  1.设定运算符栈；
  2.从左到右遍历中缀表达式的每个数字和运算符；
  3.若当前字符是数字，则直接输出成为后缀表达式的一部分；
  4.若当前字符为运算符，则判断其与栈顶运算符的优先级，若优先级大于栈顶运算符，则进栈；若优先级小于等于栈顶运算符，退出栈顶运算符成为后缀表达式的一部分，然后将当前运算符放入栈中；
  5.若当前字符为“(”，进栈；
  6.若当前字符为“)”，则从栈顶起，依次将栈中运算符出栈成为后缀表达式的一部分，直到碰到“(”。将栈中“(”出栈，不需要成为后缀表达式的一部分，然后继续扫描表达式直到最终输出后缀表达式为止。

2.1.2 栈的应用-四则运算表达式求值示例

  1、初始化一个空栈。此栈用来对运算符进出栈使用。如图2-1-2-1的左图所示。
  2、第一个字符是数字9，直接输出9（根据规则3），第二个字符是运算符“+”，则“+”进栈（根据规则4），如图2-1-2-1的右图所示。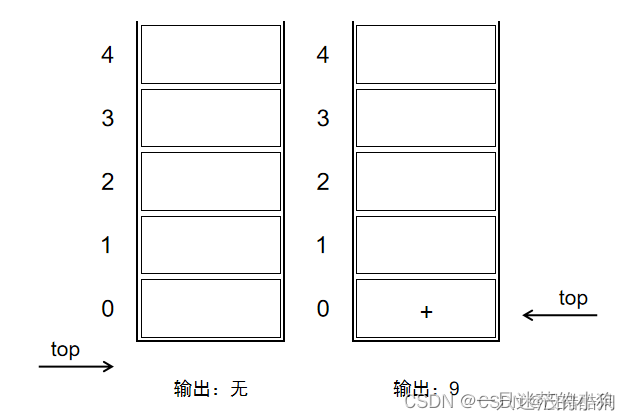

图2-1-2-1

3、第三个字符是符号“(”，则“(”进栈（根据规则5），如图2-1-2-2左图所示。

4、第四个字符是数字3，直接输出3（根据规则3），总输出表达式为

    9 3

第五个字符是运算符“-”，则“-”进栈（根据规则4），第六个字符是数字1，直接输出1（根据规则3），总输出表达式为

    9 3 1

如图2-1-2-2右图所示。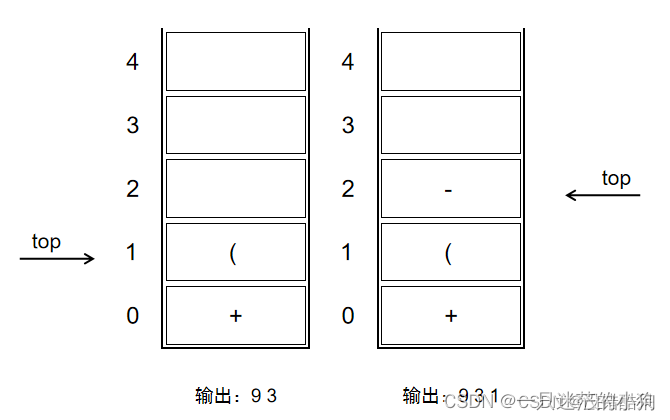


图2-1-2-2

5、第七个字符是符号“)”，此时依次将栈中运算符出栈成为后缀表达式的一部分，直到碰到"("，此时“(”上方只有“-”运算符，因此输出“-”运算符（根据规则6），总输出表达式为

    9 3 1 -

如图2-1-2-3左图所示。

  6、第八个字符是运算符“ * ”，因为此时的栈顶符号是运算符“+”，优先级低于“ * ”，因此不输出，“ * ”进栈（根据规则4），如图2-1-2-3右图所示。

图2-1-2-3

第九个字符是数字3，直接输出3（根据规则3），总输出表达式为

 9 3 1 - 3

7、第十个符号是运算符“+”，此时栈顶符号是“*”，比“+”运算符的优先级高。因此栈中元素出栈并成为后缀表达式的一部分（没有比“+”运算符更低的优先级，所以全部出栈），总输出表达式为

    9 3 1 - 3 * +

后把第十个符号“+”进栈（根据规则4）。
之前输出成为后缀表达式的“+”是中缀表达式中“9 + ”的“+”，现在入栈的“+”是中缀表达式中“9 + (3 - 1) × 3 +”的“+”。如图2-1-2-4左图所示。

  8、第十一个符号是数字8，直接输出8（根据规则3），总输出表达式为

   9 3 1 - 3 * + 8

  第十二个符号是运算符“÷”，则“/”进栈（根据规则4），如图2-1-2-4右图所示。

图2-1-2-4

 9、第十三个字符也就是最后一个字符是数字2，直接输出2（根据规则3），总输出表达式为

    9 3 1 - 3 * + 8 2

 如图2-1-2-5左图所示。

  10、因为已经到了最后一个字符，所以将栈中符号全部出栈成为后缀表达式的一部分，最终输出表达式为

    9 3 1 - 3 * + 8 2 / +

  如图2-1-2-5右图所示。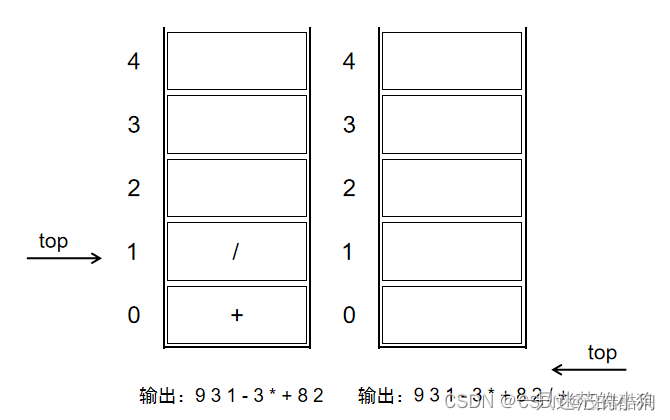

图2-1-2-5

整个过程，都充分利用了栈的后进先出特性来处理