文章目录
- 一、背景
- 二、松耦合融合策略
- 1. 信息有效性判断
- 2. 坐标系对齐
- 3. 观测方程
- a.杆臂补偿
- b.速度融合
- c.位置融合
- d. 航向yaw融合
- e.观测性分析
- 1)状态表示在VIO坐标系下的观测性分析
- 2)状态表示在GPS ENU坐标系下的观测性分析
一、背景
前面介绍了GNSS的定位原理,那么正常的GNSS模组可以解算出位置 ( G x , G y , G z ) (^Gx, ^Gy,^Gz) (Gx,Gy,Gz)以及三维速度 ( G v x , G v y , G v z ) (^Gv_x,^G v_y, ^Gv_z) (Gvx,Gvy,Gvz)以及航向角度yaw,同时也可以输出原始的GNSS测量,本文主要介绍滤波系统如何融合这些观测。
直接融合原始测量我们叫做紧耦合融合,而融合解算位姿速度结果的叫做松耦合融合。
二、松耦合融合策略
我们将坐标系转到GPS坐标系,我们这里将GPS坐标系标记为G. 变换前VIO的世界坐标系为VIO坐标系,并不是ENU,和GPS存在4 dof外参。
1. 信息有效性判断
RTK和GPS主要就是通过是否进入固定解,以及位置速度的置信度参数决定;双天线yaw的置信度也是一样,此外双天线可以判断一下解算的base_line和已知测量的baseline做个比较,或者求解的roll角度和当前飞机估计的角度作比较,去掉一些错误观测,相近才认为yaw准确。
2. 坐标系对齐
这里其实就是求解一个SE(3)的变换,求解
T
w
g
p
s
T^{gps}_{w}
Twgps坐标系变换,然后把w坐标系转成GPS坐标系即可。
求解方式很多,简单点可以直接建立一个小的优化问题,求解偏差即可,快一点的话就建立一个滤波器,滤波坐标变换偏差,cov收敛即为完成收敛。
3. 观测方程
a.杆臂补偿
GPS/IMU融合中的杆臂补偿是为了将IMU测量的姿态和加速度数据与GPS测量的位置数据进行一致性对齐。由于IMU和GPS通常安装在移动平台上的不同位置,导致IMU和GPS测量的参考点存在一定的偏移,因此需要进行杆臂补偿。主要是转弯时,刚体速度需要补偿。
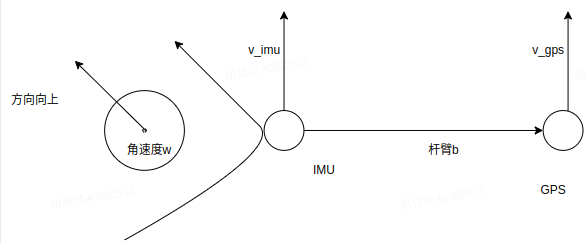
v
g
p
s
=
v
i
m
u
+
b
×
w
v_{gps} = v_{imu}+b\times w
vgps=vimu+b×w,后文用到的杆臂为
t
g
p
s
i
m
u
t_{gps}^{imu}
tgpsimu。
杆臂补偿的原理是通过将IMU测量数据转换到与GPS天线在同一位置的参考点上,实现IMU和GPS数据的对齐。具体步骤如下:
-
确定杆臂向量:通过测量或者通过精确的安装参数来获取IMU测量点与GPS天线之间的距离和方向差异,得到杆臂向量b = [b_x, b_y, b_z]。
-
转换IMU测量数据:将IMU测量的加速度和角速度数据转换到与GPS天线在同一位置的参考点上。这可以通过将IMU测量数据与杆臂向量进行叉乘来实现。
-
- 加速度补偿:将IMU测量的加速度数据a_imu = [a_x_imu, a_y_imu, a_z_imu]转换为a_gps = [a_x_gps, a_y_gps, a_z_gps],其中a_gps = a_imu + b × w_imu,w_imu为IMU测量的角速度数据。
-
- 角速度补偿:将IMU测量的角速度数据w_imu = [w_x_imu, w_y_imu, w_z_imu]转换为w_gps = [w_x_gps, w_y_gps, w_z_gps],其中w_gps = w_imu。
-
融合IMU和GPS数据:将补偿后的IMU数据与GPS数据进行融合
b.速度融合
坐标系对齐之后W世界坐标系和GPSbase坐标系E对齐,我们后续都用W表示。观测方程如下:
r
=
w
v
g
p
s
m
e
a
s
−
w
v
g
p
s
=
w
v
m
e
a
s
−
(
R
i
w
s
k
e
w
(
w
m
e
a
s
−
b
g
)
t
g
p
s
i
m
u
+
w
v
)
r = ^wv_{gps_{meas}}- ^wv_{gps}=^wv_{meas}-(R_i^wskew(w_{meas} - b_g)t_{gps}^{imu}+^wv)
r=wvgpsmeas−wvgps=wvmeas−(Riwskew(wmeas−bg)tgpsimu+wv)
c.位置融合
r = w p g p s m e a s − w p g p s = w p m e a s − ( R i w t g p s i + w t i ) r = ^wp_{gps_{meas}}- ^wp_{gps} =^wp_{meas}-(R_i^wt_{gps}^{i}+^wt_i) r=wpgpsmeas−wpgps=wpmeas−(Riwtgpsi+wti)
d. 航向yaw融合
相对位置和速度融合,航线融合有一定的技巧,主要是一般状态变量中不会维护yaw,而是维护3dof的so(3)。
当前状态的R转成欧拉角Euler,观测方程为:
r
=
y
a
w
m
e
a
s
−
E
u
l
e
r
[
0
]
r = yaw_{meas} - Euler[0]
r=yawmeas−Euler[0]
下面主要介绍解析求解Jacobian矩阵时如何计算。即欧拉角关于so(3)的Jacobian矩阵。
四元数转旋转矩阵公式:

此外,一些基础公式,主这里使用JPL左手系四元数表示(Global到Local)


带入四元数转旋转公式得到

因此

此外还会用到反对称矩阵这个公式:

旋转矩阵转欧拉角如下:

忽略二阶项得到:

进而可以得到扰动项为

这里H就是R关于欧拉角求导的Jacobian矩阵,这样就可以进行covariance的转换:

要求解的
J
=
∂
E
u
l
e
r
∂
R
=
∂
R
∂
E
u
l
e
r
.
i
n
v
e
r
s
e
(
)
=
H
T
J=\frac{\partial Euler}{\partial R} = \frac{\partial R}{\partial Euler} .inverse()=H^T
J=∂R∂Euler=∂Euler∂R.inverse()=HT的第三行;关于roll,pitch求导也是一样,取第一和第二行即可。
e.观测性分析
观测性分析是滤波系统中常用的问题分析方式,如常见的VIO系统4自由度不可观等,都可以通过观测性分析得到,我们简单介绍一下融合GPS之后系统的观测性(虽然结论显而易见,全部可观,这里就是理论推导一下)。后面有时间单独写一个如何进行观测性推导的内容,这里一些基础概念就不多做介绍了。
系统的可观性(observability)是指能否通过系统的输出来完全确定系统的内部状态。一个可观性良好的控制系统意味着系统的所有状态变量都可以通过测量系统的输出来准确地估计或恢复出来。
1)状态表示在VIO坐标系下的观测性分析
IMU的error state transition matrix为:

我们使用transition matrix去propagate covariance matrix。

这里V表示正常VIO系统的世界坐标系,E表示GPS的世界坐标系,第一种我们假设状态都表示在VIO的世界坐标系V,状态向量为:

注:这里VIO坐标系也是水平的,所以
V
E
R
^E_VR
VER只有1个自由度。
视觉重投影和GPS观测的*观测方程**为:

线性化之后的预测和观测方程可以表示为

这里的state transition matrix为:

视觉观测方程对状态求解H矩阵为:

GPS观测对应H矩阵为:

合并在一起的观测矩阵为:

进而可以得到观测性矩阵为:

可以看到这个矩阵的零空间为:

一般这种零空间都比较显而易见,很容易就能拼凑出来,但是,也可以通过下面的方法判断是哪个状态的零空间。
V
x
+
x
~
=
V
′
x
^Vx + \tilde x = ^{V'}x
Vx+x~=V′x
这里求出
x
~
\tilde x
x~,然后看是不是零空间,是的话,就是这个方向不可观。以绕g重力旋转为例,我们增加扰动
V
V
′
R
=
I
+
⌊
α
g
×
⌋
^{V'}_VR = I+\left \lfloor \alpha g\times \right \rfloor
VV′R=I+⌊αg×⌋,求出
x
~
\tilde x
x~即可。

以外参项
V
E
R
^E_V\textbf{R}
VER为例,得到其
x
~
\tilde x
x~

特征位置对应扰动为

因此,初始条件的扰动
V
V
′
R
=
I
+
⌊
α
g
×
⌋
^{V'}_VR = I+\left \lfloor \alpha g\times \right \rfloor
VV′R=I+⌊αg×⌋能够变成状态的扰动,而这个扰动就是我们的零空间,所以说明绕重力旋转不可观

2)状态表示在GPS ENU坐标系下的观测性分析
此时系统坐标系为ENU坐标系,我们标志为E

此时观测性矩阵为:

对比前面的观测性矩阵:

很明显前面的零空间
n
u
l
l
(
v
M
)
null(^vM)
null(vM)不再是
E
M
^EM
EM的零空间,但他有新的零空间,还是4个自由度,主要是因为我们把GPS到VIO的4dof外参放在了状态变量中,边缘化这4dof状态,就会发现状态完全可观了。