其实严格来说推荐系统也是一种监督学习,我们需要根据已有数据进行预测,但是这种训练数据不是单纯的输入和输出问题,所以被归类为"超越监督学习"的一种?
今天去旁听了隔壁专业的机器学习课程,感觉自己的知识确实不是很系统,所以后面会找个机会把前面的代码给补充上.
下面将会介绍两种推荐系统还有一些我了解到的计算细节,以一个电影推荐为具体的案例,可能不够详细,还请多多担待啦
1.协同过滤算法:
协同过滤算法的内容很多,所以这里我们先不直接将协同过滤的情况,我们先拟定一个情景,加入我们正在做一个电影推荐网站,我们需要给一些用户推荐电影(说白了就是这个用户可能没看过这个电影,但是我们可以根据这个用户的其他相关数据和电影相关的数据来推断用户可能会给这个电影打上多少分数,从而确定要不要给这个用户推荐这个电影)
我们从头开始讲起,最后再告诉你为什么这东西叫协同过滤,而不是简简单单的监督学习
首先我们认为,用户的打分是基于这个公式
w,b代表了用户的喜好权重和偏好,而x则代表某个电影的特征数值
(1)假设已知电影的特征
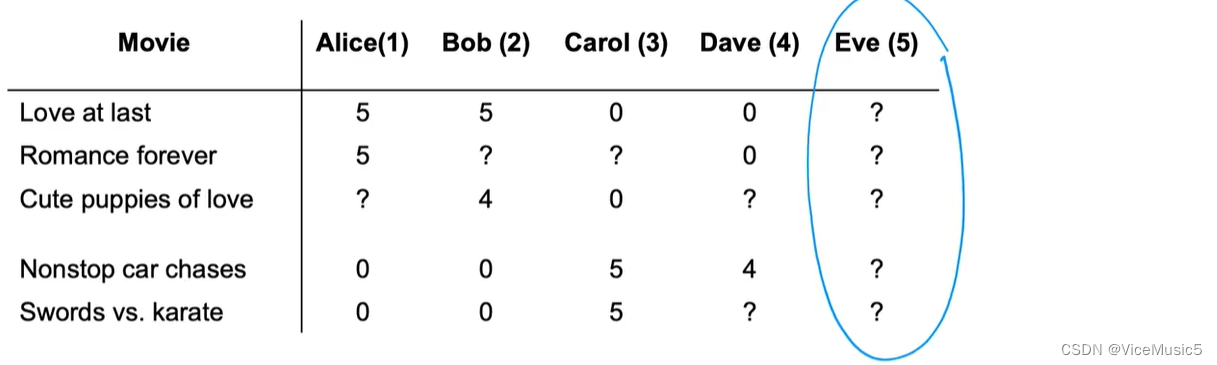
然后我们有如下的一些数据
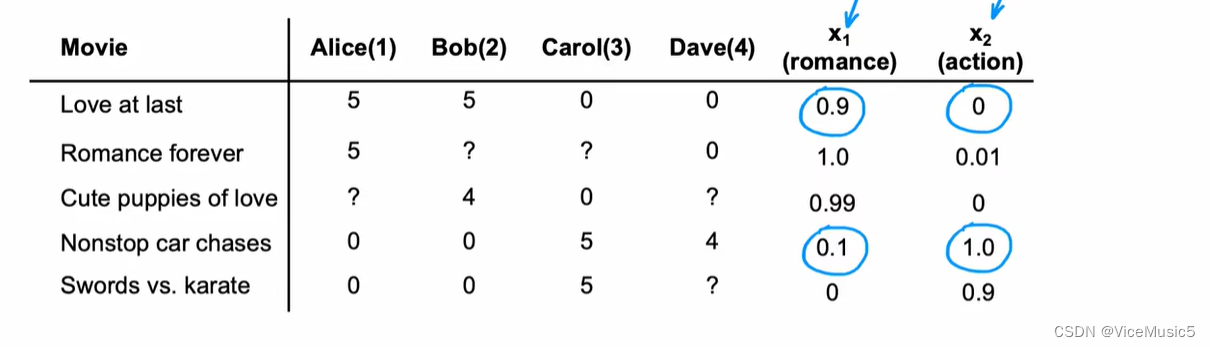
可以看到这张图里我们通过某种手段知道了电影的特征数值,比如这个电影是不是动作片,这个电影是不是浪漫电影,并且我们可以看到一些用户一些电影的打分.
我们需要预测某个用户对这个电影会打上多少分数,就必须直到整个用户的喜好,也就是我们要训练出一个合适的w和b.万幸的是,再这种图中,我们可以看到这个用户对其他电影有一些评价,我们就可以使用机器学习的手段预测出一个合适的w和b,最后再带入想要预测的电影的特征值x,就能得到用户对这个电影可能的打分.
代价函数为:(假设j为用户,i为电影)
训练出某个用户的喜好,就要用该用户看过的所有电影的特征值训练,最后对权重进行惩罚
最后得到代价最小的w和b,就可以用来估算用户的喜好了
如果是想要一次性对所有用户的喜好都进行计算,也是可行的
(2)已知用户的一些喜好
我们可以换个角度想一想,有时候上线了一部新电影,但是我们的员工没有足够的时间去看这个部电影,但是很多老客户已经打完分了,我们可以从这些了解过的老用户的打分,来推断出这个可能是什么电影.
这个时候的意思就是,我们知道很多用户的w和b,以及打分y,但是不知道某部电影的特征x.
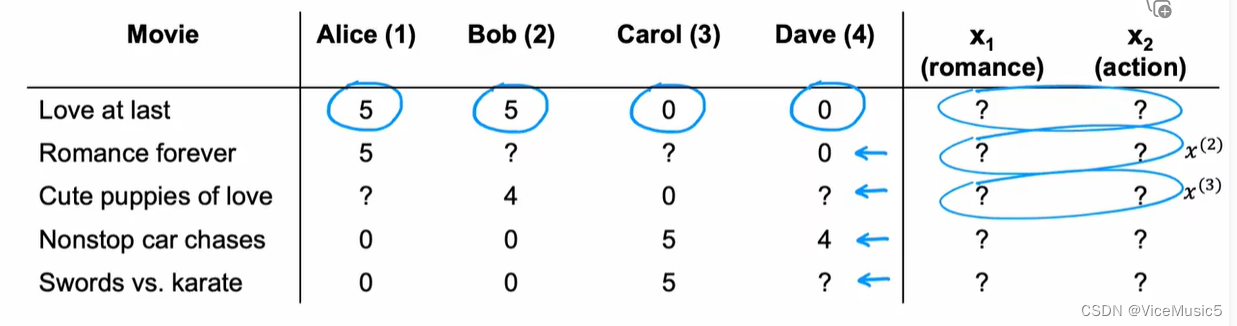
比如这张图的情况,我们只知道打分y,以及通过某种手段知道了用户的一些特征
我们就可以用类似上面的方法计算出可能的特征值
同样的,我们直接上代价函数
这个代价函数的意义就算根据所有看过这部电影的用户的打分,喜好,来判断和训练出这部电影可能的分值.
同样的,如果想要一次性囊括所有电影的代价,可以再原本的基础上加上全部的电影
这样就可以计算出电影特征值了
(3)协同过滤算法是怎么做的
这个时候你可能会问,这不就是很简单神经网络拟合吗,为什么要叫协同过滤
其实是因为第三种情况,如果我们的员工今天出去吃麦乐鸡,回来一看很多不知底细的新用户已经对新上线的电影打完分了,这个时候该怎么做推荐?就算是分开按照步骤做,我们不知道用户的喜好wb,也不知道电影的特征x,只知道用户的打分(很大概率打分都不全),然而我们仍然想要做一些推荐
答案就是综合以上两种情况,直接使用用户打分来预测其他的打分,也就是说我们要同时获取的数据是w,b,x.
还记得我们之前分别尝试过整体训练所有人的喜好和所有电影的特征,这个式子组合起来是这样的
直接把两个综合代价函数组合起来得到最终的结果.
然后具体的梯度下降操作的时候,对每个用户的喜好,每个电影的特征都要做gradient descent
这就是整体梯度下降的方法,最终合适的迭代结果可以用来估计出某个用户的某个电影的评分
(4)均值归一化
有些时候我们会碰到这样一个情况,一个纯纯的新电影,或者一个纯纯的新用户在我们的数据里面,我们仍然要想办法给他实现一些推荐.其实空白数据强行训练完全可行,但是可能数据不是很理想
其实我们的基本思想是想办法按照大家的平均值,给他来个预测打分,实际实现有点这个意思,但是不多
首先我们计算出对各个电影,看过的用户打分的平均值
然后,矩阵中原有的数据全部减去对应的平均值
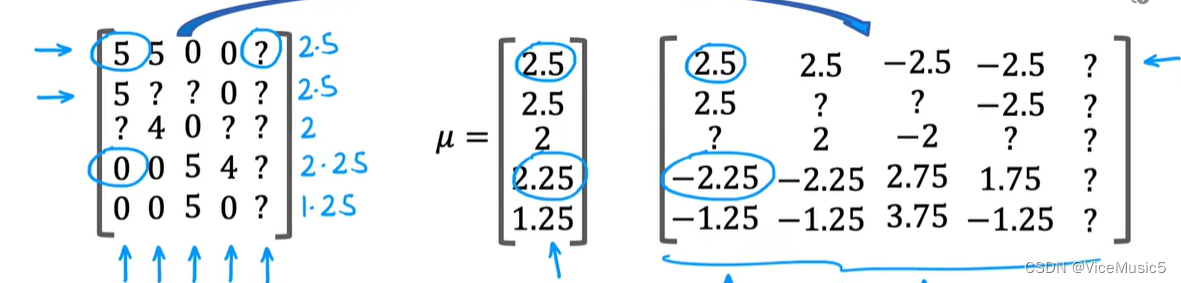
则接下来的,用户对于某个电影的估计评分,要再把平均值加回来
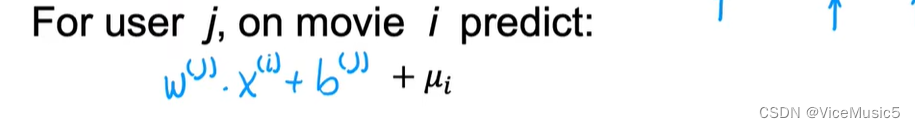
剩下的代价函数计算一致,这种方法叫做均值归一化,避免了因为某个极端数据或者空白数据导致推荐效果出现很大偏差
2.基于内容的推荐算法
上面我们提到的情况是协同过滤算法,其实再本质上是基于相似度,比如用户可能有些特征上的相似度(相似度使用范式2计算,这里不细细解释了)
而在基于内容过滤中,如果我们想要推荐一个显影,我们需要检测的是用户和电影的匹配程度,best match.
由于这个没有计算和理解上的难度,所以我们直接将具体的算法推荐出来
假设我们还是做点听推荐,与之不同的是这次我们知道用户的喜好和电影的特征,我们可以根据数据对来进行训练
((w,b,x),y)这样的数据,结合两个神经网络最终得到合适的一个训练模型,接下来就可以根据这个模型判断最终的计算结果,得到用户的可能打分
我们首先把用户特征和电影特征转化为另一种统一的形式,使用向量v来表示
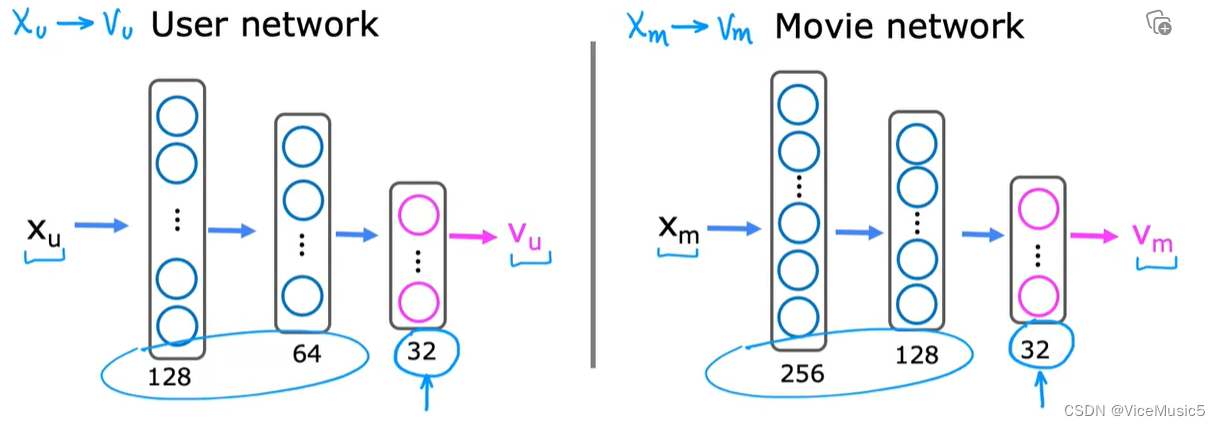
然后这两个直接相乘,就是我们的预测分数 y
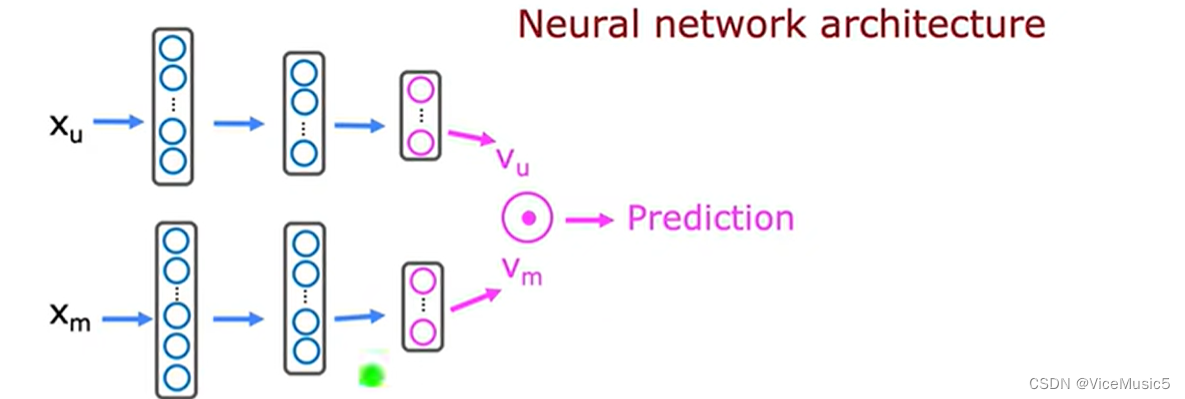
接下来根据训练数据,训练这个模型即可
3.大型目录系统的推荐
基于上面的内容过滤算法,我们可以检查用户和电影的匹配程度
但是有个问题,一个成熟的流媒体可能会产生大量的电影或者上百万的商品,进行匹配度深度网络计算,然后再排序放出来,无疑是很大的消耗,所以在一般的大型推荐系统中,我们走的是retrieve和rank两个步骤
(1)retrieve 获取一个初步的list,包含了用户可能喜欢的部分
比如从用户最近看过的10部电影,在寻找十个相似的电影
本地区的用户看到的前10个电影,或者说是每个系列最高的十部电影
(2)rank,计算用户和这个list的匹配程度,然后进行排序推荐即可
这样就避免了对于整体的排序推荐