一、换元积分法

分子分母同时除以$x{}^2$。

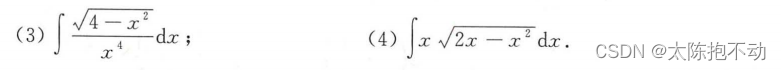
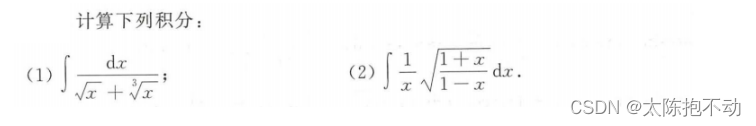
当根号下内容无法用第一类换元积分（凑微分法）和第二类换元积分法处理时，可以直接令根号等于t进行计算。

本题第一问在拆分时可以使用多项式除法。

二、分部积分法

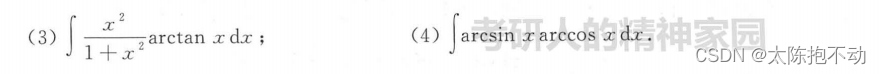
本题第三问分母使用倍角公式，化简后再拆分求解积分。

三、两类特殊函数的不定积分——有理函数与有理三角函数

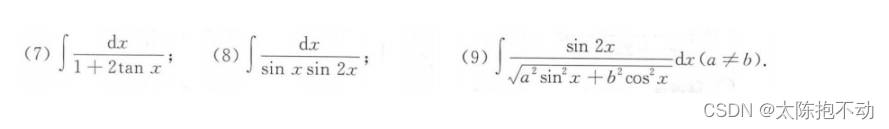
本题第(7)问，令x = tan u，积分就变成了有理函数的积分。第(8)问，分子上的1 = sin²x + cos²x。第(9)问需要明确(a²sin²x + b²cos²x)’ = (a² - b²)sin 2x。

四、分段函数的积分

分段函数的积分就是分段求出函数表达式，然后积分，最终积分结果也是分段的，这里用一个简单的例子来说明。

五、综合型不定积分

本题令x = tan u。

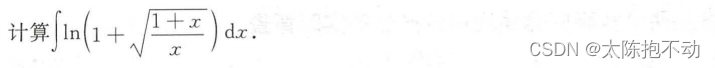
本题令根号等于t。

六、总结

这里简单总结一下

从目前做的题目来看，计算不定积分时

• 题目中出现根号时，不知道如何化简，可以直接令根号等于t。
• 题目中出现tan x时，不知道如何化简，可以令t = tan x。
• 题目中出现arctan x时，不知道如何化简，可以令x = tan x，arctan(tan x) = x。