浙大陈越何钦铭数据结构08-图7 公路村村通【循环和最小堆版】

news2024/10/1 3:36:02

题目

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

输入格式:
输入数据包括城镇数目正整数N（≤1000）和候选道路数目M（≤3N）；随后的M行对应M条道路，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见，城镇从1到N编号。

输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出−1，表示需要建设更多公路。

输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12

分析：
一个典型的最小生成树问题，可以用Prim或Kruskal实现，本文使用Prim用循环和最小堆2种方式实现。

循环代码：

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTEX_NUM 1000
#define INFINITY 65535
#define ERROR -1

typedef int Vertex;
typedef int WeightType;

struct _Edge
{
    Vertex V, W;
    WeightType weight;
};
typedef struct _Edge *Edge;

typedef struct _AdjNode *AdjNode;
struct _AdjNode
{
    Vertex adjV;
    WeightType weight;
    AdjNode next;
};

typedef struct AdjTable
{
    AdjNode firstEdge;
} AdjTable[MAX_VERTEX_NUM];

struct _LGraph
{
    int Nv, Ne;
    AdjTable graph;
};
typedef struct _LGraph *LGraph;

LGraph CreateGraph(int vertexNum);
void InsertEdge(LGraph graph, Edge E);
LGraph BuildGraph(int vertexNum, int edgeNum);
Vertex FindMinDist(LGraph G, WeightType dist[]);
int Prim(LGraph graph, Vertex S);

/*
08-图7 公路村村通
难度：1星

6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3

12

6 4
1 2 5
1 3 3
1 4 7
5 6 2


6 6
1 2 10
2 4 20
3 4 30
1 3 40
1 4 50
2 3 60

4 4
1 2 10
2 3 20
3 4 30
1 4 40

4 6
1 2 10
1 3 40
1 4 50
2 3 60
2 4 20
3 4 30
60

2 1
1 2 10


7 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 13

7 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 13

 */

int main()
{
    int N, M;
    scanf("%d %d", &N, &M);
    LGraph G = BuildGraph(N, M);
    printf("%d\n", Prim(G, 0));
    free(G);

    return 0;
}

LGraph CreateGraph(int vertexNum)
{
    LGraph G;
    G = (LGraph)malloc(sizeof(struct _LGraph));
    G->Nv = vertexNum;
    G->Ne = 0;

    for (int V = 0; V < G->Nv; V++)
    {
        G->graph[V].firstEdge = NULL;
    }

    return G;
}

void InsertEdge(LGraph G, Edge E)
{
    AdjNode NewNode;

    NewNode = (AdjNode)malloc(sizeof(struct _AdjNode));
    NewNode->adjV = E->W;
    NewNode->weight = E->weight;
    NewNode->next = G->graph[E->V].firstEdge;
    G->graph[E->V].firstEdge = NewNode;

    NewNode = (AdjNode)malloc(sizeof(struct _AdjNode));
    NewNode->adjV = E->V;
    NewNode->weight = E->weight;
    NewNode->next = G->graph[E->W].firstEdge;
    G->graph[E->W].firstEdge = NewNode;
}

LGraph BuildGraph(int vertexNum, int edgeNum)
{
    LGraph G = CreateGraph(vertexNum);
    G->Ne = edgeNum;
    Edge E;
    E = (Edge)malloc(sizeof(struct _Edge));

    for (int i = 0; i < G->Ne; i++)
    {
        scanf("%d %d %d", &E->V, &E->W, &E->weight);
        E->V--;
        E->W--;
        InsertEdge(G, E);
    }

    free(E);

    return G;
}

Vertex FindMinDist(LGraph G, WeightType dist[])
{ /* 返回未被收录顶点中dist最小者 */
    Vertex minV, V;
    WeightType minDist = INFINITY;

    for (V = 0; V < G->Nv; V++)
    {
        if (dist[V] != 0 && dist[V] < minDist)
        {
            /* 若V未被收录，且dist[V]更小 */
            minDist = dist[V]; /* 更新最小距离 */
            minV = V;          /* 更新对应顶点 */
        }
    }

    if (minDist < INFINITY) /* 若找到最小dist */
        return minV;        /* 返回对应的顶点下标 */
    else
        return ERROR; /* 若这样的顶点不存在，返回-1作为标记 */
}

int Prim(LGraph G, Vertex S)
{ // 只计算TotalWeight，无需实际创建生成树
    WeightType dist[G->Nv], totalWeight;
    Vertex V;
    AdjNode W;
    int vCount;

    for (V = 0; V < G->Nv; V++)
        dist[V] = INFINITY;

    for (W = G->graph[S].firstEdge; W; W = W->next)
        dist[W->adjV] = W->weight;

    totalWeight = 0;
    vCount = 0;

    dist[S] = 0;
    vCount++;

    while (1)
    {
        V = FindMinDist(G, dist);
        if (V == ERROR)
            break;
        totalWeight += dist[V];
        dist[V] = 0;
        vCount++;

        for (W = G->graph[V].firstEdge; W; W = W->next)
        {
            if (dist[W->adjV] != 0)
            {
                if (W->weight < dist[W->adjV])
                {
                    dist[W->adjV] = W->weight;
                }
            }
        }
    }

    if (vCount < G->Nv) /* MST中收的顶点少于|V|-1个 */
        totalWeight = ERROR;

    return totalWeight;
}

最小堆代码：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MIN_DATA -1000
#define ELEMENT_TYPE int
#define MAX_VERTEX_NUM 1000
#define INFINITY 65535
#define ERROR -1

typedef int Vertex;
typedef int WeightType;

struct _MinHeap
{
    ELEMENT_TYPE *Elements;
    int Size;
    int Capacity;
};
typedef struct _MinHeap *MinHeap;

struct _Edge
{
    Vertex V, W;
    WeightType weight;
};
typedef struct _Edge *Edge;

typedef struct _AdjNode *AdjNode;
struct _AdjNode
{
    Vertex adjV;
    WeightType weight;
    AdjNode next;
};

typedef struct AdjTable
{
    AdjNode firstEdge;
} AdjTable[MAX_VERTEX_NUM];

struct _LGraph
{
    int Nv, Ne;
    AdjTable graph;
};
typedef struct _LGraph *LGraph;

MinHeap CreateHeap(int MaxSize);
bool isEmpty(MinHeap H);
bool isFull(MinHeap H);
ELEMENT_TYPE DelMin(MinHeap H, int dist[]);
void BuildMinHeap(MinHeap H, int dist[]);
void PercUp(MinHeap H, int p, int dist[]);

LGraph CreateGraph(int vertexNum);
void InsertEdge(LGraph graph, Edge E);
LGraph BuildGraph(int vertexNum, int edgeNum);

void UpdateHeap(MinHeap H, int dist[], Vertex V);
Vertex FindMinDist(MinHeap H, int dist[]);
int Prim(LGraph graph, Vertex S);

/*
08-图7 公路村村通
难度：2星

6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3

12


6 4
1 2 5
1 3 3
1 4 7
5 6 2


4 4
1 2 10
2 3 20
3 4 30
1 4 40

4 6
1 2 10
1 3 40
1 4 50
2 3 60
2 4 20
3 4 30

60

7 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 13


 */

int main()
{
    int N, M;
    scanf("%d %d", &N, &M);
    LGraph G = BuildGraph(N, M);
    printf("%d\n", Prim(G, 0));
    free(G);

    return 0;
}

LGraph CreateGraph(int vertexNum)
{
    LGraph G;
    G = (LGraph)malloc(sizeof(struct _LGraph));
    G->Nv = vertexNum;
    G->Ne = 0;

    for (int V = 0; V < G->Nv; V++)
    {
        G->graph[V].firstEdge = NULL;
    }

    return G;
}

void InsertEdge(LGraph G, Edge E)
{
    AdjNode newNode;

    newNode = (AdjNode)malloc(sizeof(struct _AdjNode));
    newNode->adjV = E->W;
    newNode->weight = E->weight;
    newNode->next = G->graph[E->V].firstEdge;
    G->graph[E->V].firstEdge = newNode;

    newNode = (AdjNode)malloc(sizeof(struct _AdjNode));
    newNode->adjV = E->V;
    newNode->weight = E->weight;
    newNode->next = G->graph[E->W].firstEdge;
    G->graph[E->W].firstEdge = newNode;
}

LGraph BuildGraph(int vertexNum, int edgeNum)
{
    LGraph G = CreateGraph(vertexNum);
    G->Ne = edgeNum;
    Edge E;
    E = (Edge)malloc(sizeof(struct _Edge));

    for (int i = 0; i < G->Ne; i++)
    { // 用E->V--，E->W--解决顶点序号从1开始的问题
        scanf("%d %d %d", &E->V, &E->W, &E->weight);
        E->V--;
        E->W--;
        InsertEdge(G, E);
    }

    free(E);

    return G;
}

Vertex FindMinDist(MinHeap H, int dist[])
{
    Vertex minV = ERROR;

    // 从堆中取出最小值，并维护最小堆的有效性。
    minV = DelMin(H, dist);

    return minV;
}

int Prim(LGraph G, Vertex S)
{ // 只计算TotalWeight，无需实际创建生成树
    WeightType dist[G->Nv], totalWeight;
    Vertex V;
    AdjNode W;
    int vCount;

    for (V = 0; V < G->Nv; V++)
        dist[V] = INFINITY;

    for (W = G->graph[S].firstEdge; W; W = W->next)
        dist[W->adjV] = W->weight;

    totalWeight = 0;
    vCount = 0;

    dist[S] = 0;
    vCount++;

    // 根据dist对未收录顶点创建最小堆
    MinHeap H = CreateHeap(G->Nv);

    for (V = 0; V < G->Nv; V++)
    {
        if (dist[V] != 0)
        { // H->Elements保存的是未收集顶点的编号，本例依次是1,2,3
            H->Elements[++H->Size] = V;
        }
    }

    BuildMinHeap(H, dist);

    while (1)
    {
        V = FindMinDist(H, dist);
        if (V == ERROR)
            break;
        totalWeight += dist[V];
        dist[V] = 0;
        vCount++;

        for (W = G->graph[V].firstEdge; W; W = W->next)
        {
            if (dist[W->adjV] != 0)
            {
                if (W->weight < dist[W->adjV])
                { /*目标是调整H->Elements,改了吗？没有，也没有必要
                 H-Elements保存的是顶点。现在要做的是定位到W->adjV对应顶点，做percup
                   */
                    dist[W->adjV] = W->weight;
                    UpdateHeap(H, dist, W->adjV);
                }
            }
        }
    }

    if (vCount < G->Nv) /* MST中收的顶点少于|V|-1个 */
        totalWeight = ERROR;

    return totalWeight;
}

MinHeap CreateHeap(int MaxSize)
{
    MinHeap H = (MinHeap)malloc(sizeof(struct _MinHeap));
    H->Elements = (ELEMENT_TYPE *)malloc((MaxSize + 1) * sizeof(ELEMENT_TYPE));
    H->Elements[0] = MIN_DATA;
    H->Size = 0;
    H->Capacity = MaxSize;

    return H;
}

bool isEmpty(MinHeap H)
{
    return H->Size == 0;
}

bool isFull(MinHeap H)
{
    return H->Size == H->Capacity;
}

ELEMENT_TYPE DelMin(MinHeap H, int dist[])
{
    if (!isEmpty(H))
    {
        ELEMENT_TYPE min, last;
        int parent, child;

        min = H->Elements[1];
        last = H->Elements[H->Size--];

        for (parent = 1; 2 * parent <= H->Size; parent = child)
        {
            child = 2 * parent;
            if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]]))
            {
                child++;
            }
            if (dist[last] <= dist[H->Elements[child]])
            {
                break;
            }
            else
            {
                H->Elements[parent] = H->Elements[child];
            }
        }

        H->Elements[parent] = last;

        if (dist[min] < INFINITY)
            return min;
        else
            return ERROR;
    }
    else
    {
        return ERROR;
    }
}

void PercUp(MinHeap H, int p, int dist[])
{ /*根据顶点的dist值，决定顶点在堆中的存储位置。
  对dist[H->Elements[child]] > dist[H->Elements[child + 1]]的理解
  dist[x] > dist[y],本质是比较两个顶点之间的dist值，x,y是顶点序号。
  dist[x]的初始值通过dist[V] = G->dist[S][V]获得，并用dist[W] = dist[V] + G->dist[V][W]更新
  child是顶点在堆中的索引，H->Elements[child]存储的是顶点序号
  所以dist[H->Elements[child]]是顶点的dist值。
  */

    int parent, child;
    ELEMENT_TYPE X;
    X = H->Elements[p];

    for (parent = p; 2 * parent <= H->Size; parent = child)
    {
        child = 2 * parent;
        if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]]))
        {
            child++;
        }
        if (dist[X] <= dist[H->Elements[child]])
        {
            break;
        }
        else
        {
            H->Elements[parent] = H->Elements[child];
        }
    }

    H->Elements[parent] = X;
}

void BuildMinHeap(MinHeap H, int dist[])
{ // p表示顶点在堆中的位置
    int p;
    for (p = H->Size / 2; p > 0; p--)
    {
        PercUp(H, p, dist);
    }
}

void UpdateHeap(MinHeap H, int dist[], Vertex V)
{
    int i, idx, x;

    // 找到V在堆中的位置
    for (i = 1; i <= H->Size; i++)
    {
        if (H->Elements[i] == V)
        {
            idx = i;
            x = dist[H->Elements[idx]];
            break;
        }
    }
    // 更新V的dist值，并向上调整堆
    // dist[V] = dist[H->Elements[i]];
    /* 是否需要条件i>1？
     */
    for (i = idx; i > 1 && dist[H->Elements[i / 2]] > x; i /= 2)
    {
        H->Elements[i] = H->Elements[i / 2];
    }

    H->Elements[i] = V;
}

小结:
典型的Prim应用，姥姥没有讲最小堆的具体实现，代码磨了很久，终于过了。简言之，只有对最小生成树算法逻辑有深刻的认识，同时有足够的耐心和细心，实际动手写，才能提高代码能力。

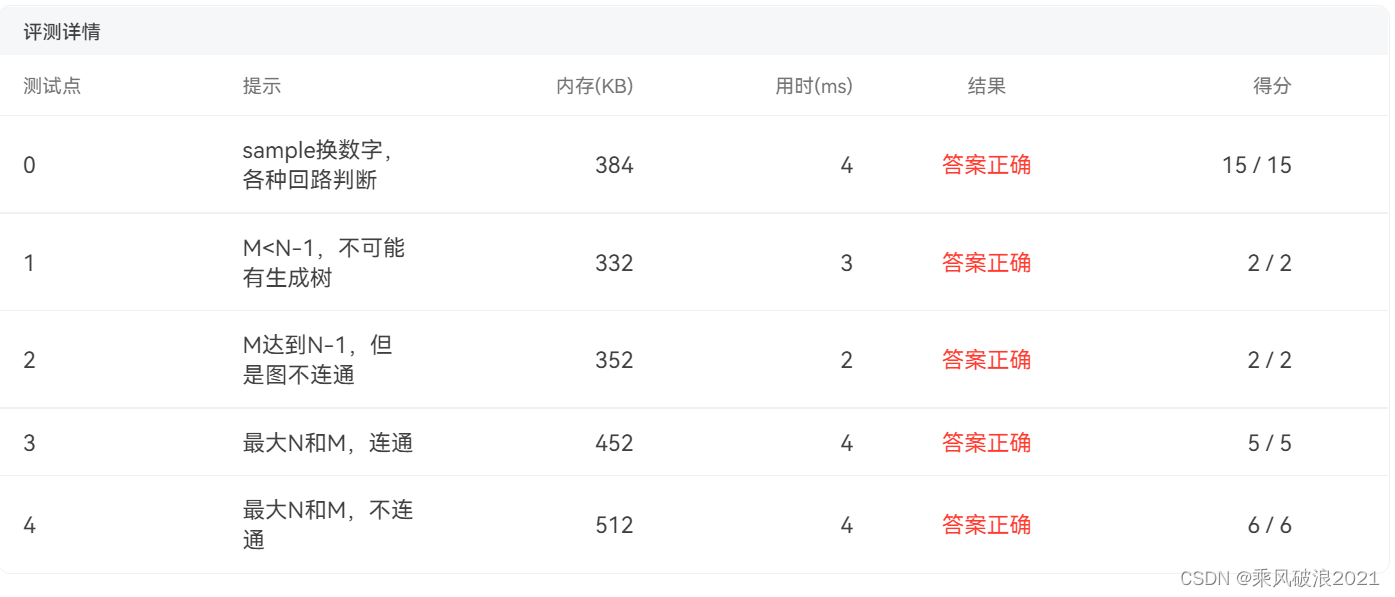
结果：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/983775.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

.netcore对传输类设置区分大小

.netcore对传输类设置区分大小

.Net Core中内置了对Json的转化与解析 可将PropertyNameCaseInsensitive false 设置为区分大小写。
阅读更多...
socket的使用 | 服务器与客户端之间传送数据

socket的使用 | 服务器与客户端之间传送数据

服务器端代码&#xff1a; import java.io.*; import java.net.ServerSocket; import java.net.Socket;public class theServer {public static void main(String[] args) throws IOException {ServerSocket serverSocket new ServerSocket(9999); // 该行代码作用&#xff1…
阅读更多...
IGES在线查看与转换

IGES在线查看与转换

IGES 格式最初由美国空军开发并于 1980 年发布。该格式是集成计算机辅助制造 (ICAM) 项目的产品，该项目旨在通过集成操作来降低制造成本。 IGES 文件旨在允许航空航天相关设计在不同平台上传输，同时将数据丢失降至最低。 在 IGES 格式出现之前，不同公司创建的 CAD 和计算机…
阅读更多...
PPT怎么转换为PDF格式，收藏这两个在线工具。

PPT怎么转换为PDF格式，收藏这两个在线工具。

PPT是一种常用的演示文稿格式&#xff0c;它可以包含丰富的动画效果和超链接&#xff0c;让你的内容更加生动和有趣。但是&#xff0c;如果你想将PPT分享给别人&#xff0c;或者在不同的设备上查看&#xff0c;你可能会遇到一些问题&#xff0c;比如&#xff1a; PPT文件太大&a…
阅读更多...
按照xml文件和txt文件名，将对应名字的图象文件复制

按照xml文件和txt文件名，将对应名字的图象文件复制

按照xml文件和txt文件名&#xff0c;将对应名字的图象文件复制 需求分析解决方案 需求分析 就是已经标注了xml和txt文件&#xff0c;需要将其对应的图象文件挑选出来 解决方案 # 按照xml文件删除对应的图片 # coding: utf-8 from PIL import Image, ImageDraw, ImageFont imp…
阅读更多...
【多线程】线程安全与线程同步

【多线程】线程安全与线程同步

线程安全与线程同步 1.什么是线程安全问题&#xff1f; 多个线程同时操作同一个共享资源的时候&#xff0c;可能会出现业务安全问题 取钱的线程安全问题场景&#xff1a; 两个人他们有一个共同的账户&#xff0c;余额是10万元&#xff0c;如果两个人同时来取钱&#xff0c;…
阅读更多...
国内某头部理财服务提供商基于白鲸调度系统建立统一调度和监控运维

国内某头部理财服务提供商基于白鲸调度系统建立统一调度和监控运维

导读&#xff1a;国内某头部理财服务提供商成立于 2019 年&#xff0c;是股份制银行中首批获准筹建、首家获准开业、首家成立的银行理财子公司。自 2004 年推出国内首支人民币理财产品以来&#xff0c;通过投资模式的不断创新和投资管理能力的持续提升&#xff0c;引领国内银行…
阅读更多...
Vue2项目练手——通用后台管理项目第七节

Vue2项目练手——通用后台管理项目第七节

Vue2项目练手——通用后台管理项目 用户管理分页使用的组件Users.vuemock.js 关键字搜索区Users.vue 权限管理登录页面样式修改Login.vue 登录权限使用token对用户鉴&#xff0c;使用cookie对当前信息保存&#xff08;类似localstorage&#xff09;Login.vuerouter/index.js 登…
阅读更多...
go基础08-map的内部实现

go基础08-map的内部实现

和切片相比&#xff0c;map类型的内部实现要复杂得多。Go运行时使用一张哈希表来实现抽象的map类型。运行时实现了map操作的所有功能&#xff0c;包括查找、插入、删除、遍历等。在编译阶段&#xff0c;Go编译器会将语法层面的map操作重写成运行时对应的函数调用。 下面是大致的…
阅读更多...
07-垃圾收集算法详解

07-垃圾收集算法详解

上一篇&#xff1a;06-JVM对象内存回收机制深度剖析 1.分代收集理论 当前虚拟机的垃圾收集都采用分代收集算法&#xff0c;这种算法没有什么新的思想&#xff0c;只是根据对象存活周期的不同将内存分为几块。一般将java堆分为新生代和老年代&#xff0c;这样我们就可以根据各…
阅读更多...
【LeetCode-中等题】17. 电话号码的字母组合

【LeetCode-中等题】17. 电话号码的字母组合

文章目录 题目方法一&#xff1a;递归回溯 题目 方法一&#xff1a;递归回溯 参考讲解&#xff1a;还得用回溯算法&#xff01;| LeetCode&#xff1a;17.电话号码的字母组合 首先可以画出树图&#xff1a; 先将数字对应的字符集合 加入到一个map集合 这里需要一个index来控…
阅读更多...
【vue2第十七章】VueRouter 编程式导航跳转传参(点击按钮跳转路由和如何传递参数)

【vue2第十七章】VueRouter 编程式导航跳转传参(点击按钮跳转路由和如何传递参数)

如何在js进行跳转路由 在一些需求中&#xff0c;我们需要不用点击a标签或者router-link&#xff0c;但是也要实现路由跳转&#xff0c;比如登陆&#xff0c;点击按钮搜索跳转。那么这种情况如何进行跳转呢&#xff1f; 直接再按钮绑定的方法中写this.$router.push(路由路径)即…
阅读更多...
软件兼容性测试怎么做?对软件产品起到什么作用?

软件兼容性测试怎么做?对软件产品起到什么作用?

软件兼容性测试是一项重要的软件测试活动&#xff0c;它可以确保在不同操作系统、硬件配置和软件环境下&#xff0c;软件能够正常运行&#xff0c;并与其他相关软件和系统进行正确的互动。 一、软件兼容性的测试方法 1、操作系统测试&#xff1a;测试软件在不同操作系统上的兼…
阅读更多...
linux常用命令及解释大全（二）

linux常用命令及解释大全（二）

目录 前言 一、文件的权限 二、文件的特殊属性 三、打包和压缩文件 四、查看文件内容 五、文本处理 5.1 grep 5.2 sed 5.3 其它 总结 前言 本篇文章接linux常用命令及解释大全&#xff08;一&#xff09;继续介绍了一部分linux常用命令&#xff0c;包括文件的权限&a…
阅读更多...
Android签名查看

Android签名查看

查看签名文件信息 第一种方法&#xff1a; 1.打开cmd&#xff0c;执行keytool -list -v -keystore xxx.keystore&#xff0c;效果如下图&#xff1a; 第二种方法: 1.打开cmd&#xff0c;执行 keytool -list -v -keystore xxxx.keystore -storepass 签名文件密码&#xff0…
阅读更多...
Linux 下 C语言版本的线程池

Linux 下 C语言版本的线程池

目录 1. 线程池引入 2. 线程池介绍 3. 线程池的组成 4. 任务队列 5. 线程池定义 6. 头文件声明 7. 函数实现 8. 测试代码 1. 线程池引入 我们使用线程的时候就去创建一个线程&#xff0c;这样实现起来非常简便&#xff0c;但是就会有一个问题&#xff1a;如果并发的线程数…
阅读更多...
壁炉在文学和艺术中的代表着什么呢，能给我们带来什么样的影响？

壁炉在文学和艺术中的代表着什么呢，能给我们带来什么样的影响？

壁炉&#xff0c;不仅仅是家庭温暖的来源&#xff0c;也是文学和艺术中常见的重要元素。它的形象在文学作品、绘画和电影中频繁出现&#xff0c;不仅为故事情节提供了背景&#xff0c;还象征着情感、温馨和安全感。让我们一起深入探讨壁炉在文学和艺术中的形象&#xff0c;以及…
阅读更多...
Android相机调用-CameraX【外接摄像头】【USB摄像头】

Android相机调用-CameraX【外接摄像头】【USB摄像头】

Android相机调用有原生的Camera和Camera2&#xff0c;我觉得调用代码都太复杂了&#xff0c;CameraX调用代码简洁很多。 说明文档&#xff1a;https://developer.android.com/jetpack/androidx/releases/camera?hlzh-cn 现有查到的调用资料都不够新&#xff0c;对于外接摄像…
阅读更多...
RecyclerView的item布局预览显示是一行两块 运行后显示了一行一块，怎么回事

RecyclerView的item布局预览显示是一行两块 运行后显示了一行一块，怎么回事

QQ有人问我了&#xff1a; 没有起作用&#xff1f;有 解决问题&#xff1a;在item布局上第一个外层宽度、高度分别为match_parent和wrap_content&#xff0c;第二个外层宽度和高度都为match_parent&#xff0c;运行后可以显示一行两块 其他学习资料&#xff1a; 1、付费专栏…
阅读更多...
mybatis 数据库字段加密

mybatis 数据库字段加密

目录 1、引入依赖 2、添加配置 3、指定加密字段 4、测试&#xff0c;效果 1、引入依赖 <dependency><groupId>io.github.whitedg</groupId><artifactId>mybatis-crypto-spring-boot-starter</artifactId><version>1.2.3</version>…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023