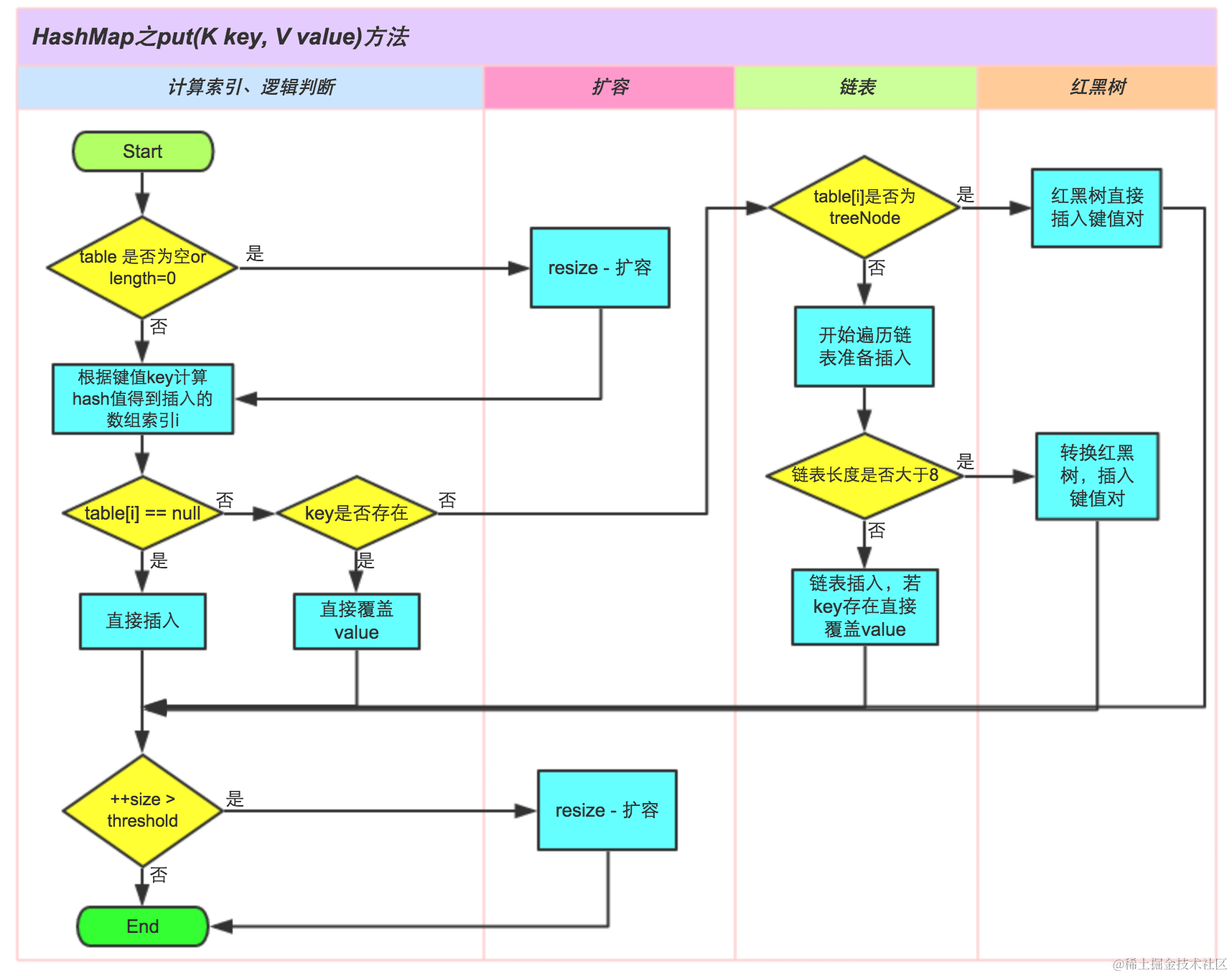
合并区间
- 题解1 左端点排序后合并(可证连续,贪心)
- 题解2 双指针(优化)
以数组 i n t e r v a l s intervals intervals 表示若干个区间的集合,其中单个区间为 i n t e r v a l s [ i ] = [ s t a r t i , e n d i ] intervals[i] = [starti, endi] intervals[i]=[starti,endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
- 1 <= i n t e r v a l s . l e n g t h intervals.length intervals.length <= 104
- i n t e r v a l s [ i ] . l e n g t h intervals[i].length intervals[i].length == 2
- 0 <= s t a r t i start_{i} starti <= e n d i end_{i} endi <= 104
题解1 左端点排序后合并(可证连续,贪心)
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
int s = intervals.size();
if(1 == s) return intervals;
vector<vector<int>> res;
/* sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b) -> bool {
return a[0] < b[0];
});
*/
sort(intervals.begin(), intervals.end());
for(int i = 0; i < s; i++){
if(! res.size() || res.back()[1] < intervals[i][0]){
// 不能合并,直接加入res
res.push_back(intervals[i]);
}
else {
// 能合并,右边界取最大值
res.back()[1] = max(res.back()[1], intervals[i][1]);
}
}
return res;
}
};
题解2 双指针(优化)
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
int s = intervals.size();
if(1 == s) return intervals;
vector<vector<int>> res;
sort(intervals.begin(), intervals.end());
// 双指针设置
int slow = 0, fast = 0;
while(slow < s){
// fast每次都比slow大1(往前探)
fast ++;
int t = intervals[slow][1];
// key:左端点排序后,只需要往后找满足条件的右端点(只要当前右端>其他左端,即重叠)
while(fast < s && t >= intervals[fast][0]){
t = max(t, intervals[fast][1]);
fast ++;
}
res.emplace_back(vector<int>{intervals[slow][0], t});
// 更新慢指针
slow = fast;
}
return res;
}
};