一、均值滤波

# 卷积操作
# 输入图片. input, 必须是4维tensor(图片数量, 图片高度, 图片的宽度, 图片的通道数)
# filters, 卷积核, 必须是4维的tensor(卷积核的高度和宽度, 输入图片的通道数, 卷积核的个数)
# strides, 步长, 卷积核在图片的各个维度上的移动步长, (1, 1, 1, 1)
# padding, 0填充, 'Valid'和'Same', valid表示不进行填充, same表示输入图片和输出图片大小保持一致.
# 输入数据的格式: data_format 'NHWC'
# tf.nn.conv2d()

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf


moon = plt.imread('/newdisk/darren_pty/CNN/moonlanding.png')
print(moon.shape)

plt.figure(figsize=(10, 8))
plt.imshow(moon, cmap='gray')

plt.show()

plt.imshow是用来显示图像的函数,它可以将数组或矩阵转化为图像并显示。

plt.show是用来显示图像的函数,它会打开一个窗口来显示当前的图像,只有调用了这个函数,图像才会真正显示出来。

简单来说,plt.imshow是将数据变成图像,plt.show是将图像显示出来。

plt.figure("Image")  创建图像窗口

均值滤波：

np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]) //3x3 的矩阵

使用这样的矩阵来执行平滑操作，通过将每个像素的值替换为其周围像素值的平均值来减小图像中的噪声或细节。这个操作称为均值滤波。

np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1)

将这个矩阵重新塑造成一个 4 维数组，形状为 (3, 3, 1, 1)。

# 均值滤波
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype=tf.float32)
filters = tf.constant(np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1), dtype=tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input=input_img, filters=filters, strides=strides, padding='SAME')
plt.figure(figsize=(10, 8))

# 4维图片转为2维图像
plt.imshow(conv2d.numpy().reshape(474, 630), cmap='gray') 

 

`tf.constant` 是 TensorFlow 中的一个函数，用于创建一个常量张量（tensor）。在 TensorFlow 中，张量是多维数组，可以包含标量、向量、矩阵等。

`tf.constant` 的基本语法如下：

tf.constant(value, dtype=None, shape=None, name='Const', verify_shape=False)

参数说明：

- `value`：要创建的常量张量的值。可以是 Python 中的标量、列表、NumPy 数组或其他 TensorFlow 张量。
- `dtype`：可选参数，指定常量的数据类型。例如，`tf.float32` 表示浮点数类型，默认为 `tf.float32`。
- `shape`：可选参数，指定常量张量的形状。如果未指定，则根据 `value` 的形状自动确定。
- `name`：可选参数，为常量张量指定名称。
- `verify_shape`：可选参数，如果为 True，则会检查 `value` 是否具有与指定 `shape` 匹配的形状。默认为 False。

以下是一些示例：

import tensorflow as tf

# 创建一个标量常量
scalar_constant = tf.constant(5)

# 创建一个形状为 (2, 3) 的常量张量
matrix_constant = tf.constant([[1, 2, 3], [4, 5, 6]])

# 创建一个形状为 (3, 2) 的常量张量，并指定数据类型为 float32
float_matrix_constant = tf.constant([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]], dtype=tf.float32)

`tf.constant` 用于创建不可变的张量，即创建后无法更改其值。如果你需要可变的张量，可以使用其他 TensorFlow 操作来实现，例如 `tf.Variable`。

二、高斯滤波

高斯滤波的卷积核具有以下特点：

1. **中心点权重最高**：高斯滤波核的中心点权重最高，而周围的权重逐渐减小。这是因为高斯分布在中心点处具有峰值，而在距离中心点越远的位置权重逐渐减小。

2. **对称性**：高斯滤波核通常是对称的，即以中心点为对称轴，左右或上下的权重是相等的。这确保了平滑操作是均匀的，不引入图像的偏移或拉伸。

3. **权重和为1**：高斯滤波核的所有权重之和始终为1。这确保了在滤波过程中图像的亮度不会发生明显的变化，因为它们都是加权平均值。

4. **标准差控制平滑程度**：高斯滤波核的平滑程度由标准差（σ，sigma）参数控制。较小的标准差会产生较低的平滑效果，而较大的标准差会产生更高的平滑效果。标准差越大，权重分布越广，导致更大程度的平滑。

5. **核的大小**：高斯滤波核的大小通常是一个奇数，例如3x3、5x5等。核的大小决定了平滑的程度，较大的核可以产生更强烈的平滑效果。

高斯滤波核的形状和权重分布使其能够有效地去除图像中的高频噪声，平滑图像，并保持图像的整体结构。这使得它成为图像处理和计算机视觉中常用的滤波方法之一，特别是在前处理步骤中用于减少噪声以提高后续处理步骤的性能。

# 高斯滤波
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype=tf.float32)
filters = tf.constant(np.array([[1/9, 2/9, 1/9], [2/9, 3/9, 2/9], [1/9, 2/9, 1/9]]).reshape(3, 3, 1, 1), dtype=tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input=input_img, filters=filters, strides=strides, padding='SAME')
plt.figure(figsize=(10, 8))
plt.imshow(conv2d.numpy().reshape(474, 630), cmap='gray')

三、边缘检测

np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])   用于进行图像边缘检测

这个特定的卷积核可以用于检测图像中的边缘特征。它的作用如下：

• 中心像素（-4）具有最高的负权重，表示它对于周围像素的差异非常敏感。
• 上、下、左、右的相邻像素（1）具有正权重，表示它们对于中心像素的影响。
• 四个对角线的相邻像素（0）没有影响。
• 通过在图像上滑动这个卷积核并执行卷积操作，可以突出图像中的边缘特征，因为边缘通常是像素值的剧烈变化。这种卷积核也可以用于图像锐化，以增强图像中的边缘特征。

cat = plt.imread('cat.jpg')
plt.figure(figsize=(10, 8))
plt.imshow(cat)

# 把猫变成黑白图片. 
cat = cat.mean(axis=2)
plt.figure(figsize=(10, 8))

#不加gray，图像将会被上色
plt.imshow(cat, cmap='gray')

 `cat.mean(axis=2)` 是一个NumPy数组操作，用于计算沿指定轴（axis）的平均值。让我们解释一下这个操作的含义：

假设 `cat` 是一个NumPy数组，它的形状为 `(height, width, channels)`，其中：
- `height` 表示图像的高度（垂直像素数）。
- `width` 表示图像的宽度（水平像素数）。
- `channels` 表示图像的通道数，通常是3（表示红、绿、蓝通道）。

`axis=2` 意味着你正在沿着第三个维度（即通道维度）计算平均值。在这个上下文中，`cat.mean(axis=2)` 将返回一个新的NumPy数组，该数组的形状为 `(height, width)`，其中每个元素代表了在相应位置的像素通道的平均值。

这个操作通常用于将彩色图像转换为灰度图像，因为它会将每个像素点的颜色通道平均值作为该像素点的灰度值，从而将彩色图像转换为灰度图像。

#不加gray，图像将会被上色

# 边缘检测
input_img = tf.constant(cat.reshape(1, 456, 730, 1), dtype=tf.float32)
filters = tf.constant(np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]).reshape(3, 3, 1, 1), dtype=tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input=input_img, filters=filters, strides=strides, padding='SAME')
plt.figure(figsize=(10, 8))
plt.imshow(conv2d.numpy().reshape(456, 730), cmap='gray')
plt.show()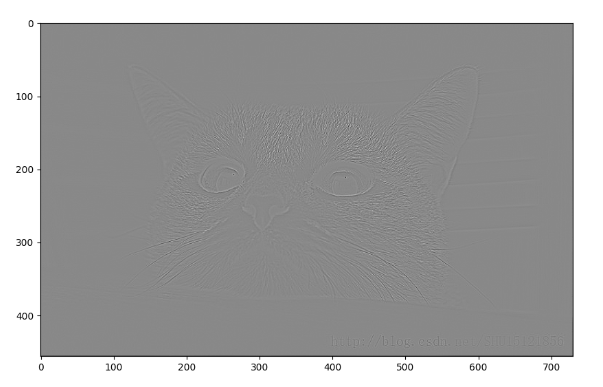

通常，神经网络中，卷积核数值是用 反向传播 计算得到

四、锐化

# 锐化
input_img = tf.constant(cat.reshape(1, 456, 730, 1), dtype=tf.float32)
filters = tf.constant(np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]]).reshape(3, 3, 1, 1), dtype=tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input=input_img, filters=filters, strides=strides, padding='SAME')
plt.figure(figsize=(10, 8))
plt.imshow(conv2d.numpy().reshape(456, 730), cmap='gray')

五、对彩色图片的卷积

彩色图片有三个通道，把每个通道作为一张图

euro.reshape(1, 582, 1024, 3).transpose([3, 1, 2, 0]) //不改变图片的情况下，修改维度

euro = plt.imread('./欧式.jpg')
plt.figure(figsize=(10, 8))
plt.imshow(euro)
print(euro.shape) #形状

# 对彩色图片进行卷积操作.
# 把彩色图片的每个通道当成一张图
input_img = tf.constant(euro.reshape(1, 582, 1024, 3).transpose([3, 1, 2, 0])), dtype=tf.float32)
filters = tf.constant(np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1), dtype=tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input=input_img, filters=filters, strides=strides, padding='SAME')
plt.figure(figsize=(10, 8))
plt.imshow(conv2d.numpy().reshape(3, 582, 1024).transpose([1, 2, 0]) / 255.0)