提出问题
- 混合数据集中深度范围的变化会导致网络的不稳定。虽然已经引入了一些仿射不变的损失函数,但现有的方法可能会导致次优的几何结构,如模糊的边界和细节。
思路
- 我们提出了一种新的像素级监督损失,称为 the windowed correlation regression loss。它计算加窗的皮尔逊(Pearson)相关系数来约束局部区域内数据分布的相似性。
- 我们引入了一种新的从粗到细的多尺度法态损失,以进一步提高几何精度。
方法
- SSI-MAE or ILNR 在同一了尺度和变换之后应用MAE损失。这样会导致模糊的边界和过度平滑的转变。相比之下,几何结构本质上是“区域化的”,这意味着可识别的结构需要由一个由区域内的所有像素组成的集体呈现。
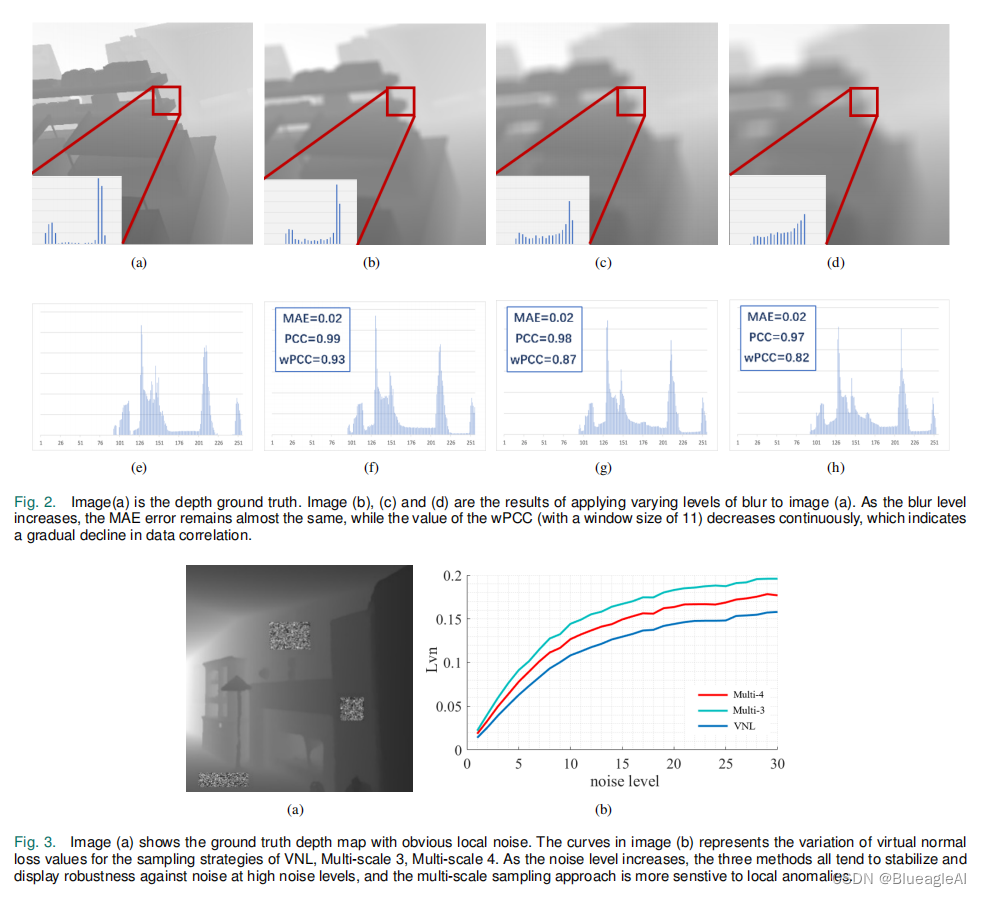
- Pearson correlation coefficient (PCC)(皮尔逊相关系数)用于统计学中,以度量数据分布之间的线性相似性,或通过灰度分布来量化图像的相似性。
- 不同的区域可能仍然表现出相似的灰度分布。因此,我们打算联合一个几何约束损失,以提供更严格的几何监督。一项令人印象深刻的工作是虚拟正常损失 Virtual Normal Loss(VNL)。
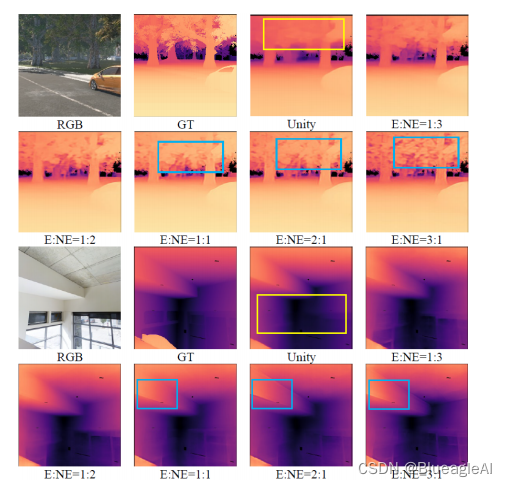
两个损失函数的工作流程
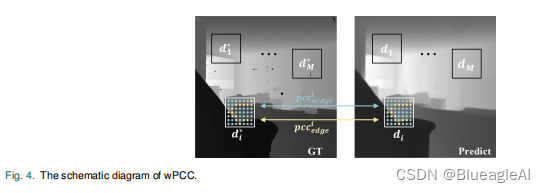
- Windowed correlation regression loss (WCR loss):深度图应根据真实标签 d ∗ d^* d∗分为边缘和非边缘块。
- 首先利用Sobel 操作提取 d ∗ d^* d∗梯度图G。然后通过阈值分割G的的得到边图G。最后,通过扩张(dilation)操作减少伪影。
- wPCC:在
d
∗
d^*
d∗上随机采样M个
s
×
s
s \times s
s×s的块,定义为
d
i
∗
d^*_i
di∗.每一个块内又有边区域
d
e
d
g
e
i
∗
d^*_{edge_i}
dedgei∗以及
d
n
e
d
g
e
i
∗
d^*_{nedge_i}
dnedgei∗。
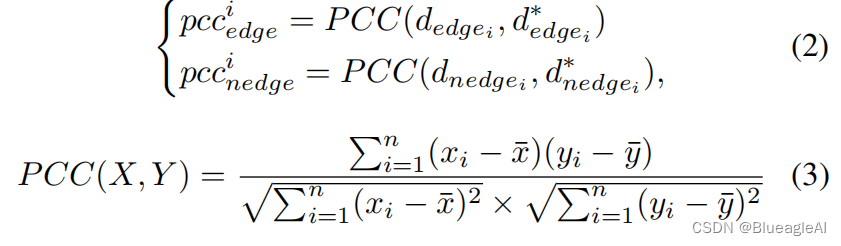
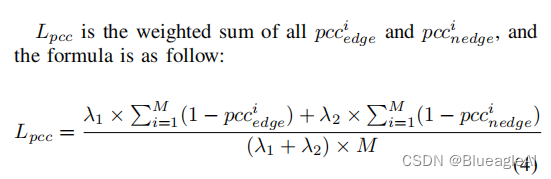

-
Coarse-to-fine multi-scale normal loss (CFMN loss):
-
首先将深度转成3D点云:
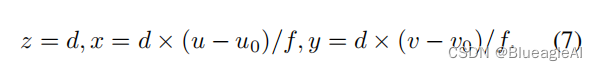
-
在m个不同尺度上采样三个点 ( P A , P B , P C ) (P_A,P_B,P_C) (PA,PB,PC), 记为 P t o t a l = U j = 1 m P s j × t j , s j = h / 2 j , t j = w / 2 j P_{total} = U^m_{j=1}P_{s_j \times t_j}, s_j = h/2^j, t_j=w/2^j Ptotal=Uj=1mPsj×tj,sj=h/2j,tj=w/2j.
-
网络通过优化视觉法向量误差最小化损失函数:
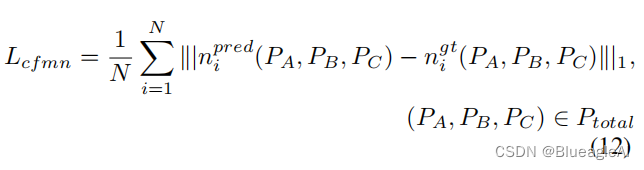
补充内容
- 皮尔逊相关系数( Pearson correlation coefficient),用于度量两个变量X和Y之间的相关(线性相关),介于[-1,1]之间。
- 两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:
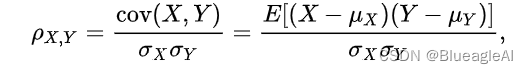
- 总体相关系数
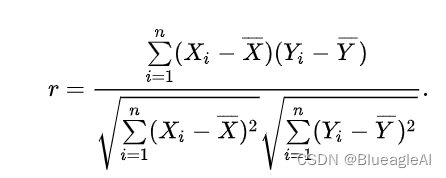
- 样本的相关系数

- 总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上(计算样本皮尔逊系数的情况),或者双变量分布完全在直线上(计算总体皮尔逊系数的情况),则相关系数等于1或-1。皮尔逊系数是对称的。
- 皮尔逊相关系数一个重要的数学特性是,因两个变量的位置和尺度的变化并不会引起该系数的改变,即它该变化的不变量(由符号确定)。也就是说,我们如果把移动到和把Y移动到 c + d Y c+dY c+dY,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)。