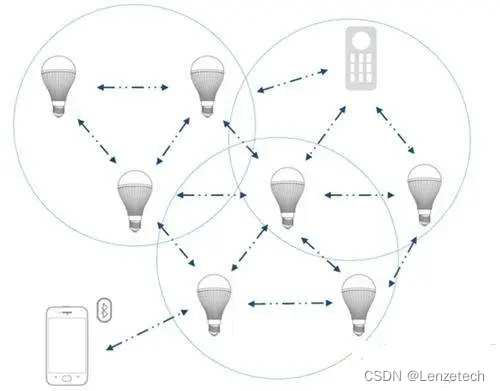
文章目录
- 解析
个人见解,如有错误,请多包涵。
解析
对于人来说,减法是简单容易的。
被减数和减数列式相减,从低位到高位分别计算,有需要的借位就可以了。
这是一种可以在计算机上成立的理论方案,但是由于减法电路相较于加法电路造价更加昂贵,将减法化为另一种加法运算是一种不错的选择。

A - B = A + (-B)
但是原码并不满足这种减法化为加法的想法,例如:2-2这个运算,应该将其化为2+(-2),但计算结果并不正确。
如果是八位的情况下,
2的原码= 0,0000010
2的补码= 1,0000010
二者相加= 1,0000100 = -4D
我们都知道2-2=0,即是将其化为2+(-2)也得等于0,但是通过原码的计算方法得出来的确实-26。
负数加上其绝对值不等于0,可怕的现象,那么保持正数的原码形式不变的前提下,它应该如何运算,加上那种对应的二进制串,才能让结果为零呢?
不妨想想,2对应的原码为0000 0010,若是将其全部按位取反,得到1111 1101,再将二者相加,那么此刻你会得到一串二进制数:1111 1111,对于八位的二进制串来说。
这是一个处在表达极限的一串数字,超出最高位的数字是不被表达的,不被记录的。那么,也就是说,如果此时再将这串二进制数+1,你将得到一串位数为九的:1 0000 0000。
因为位数只会保留八位,那么这串二进制数代表的数字与0是一样的,此时,你就已经完成了负数加上其绝对值等于0的设计。
提取一下思路,
2的原码形式保持不变,也就是正数的原码还是其本身,我们将其称为正数的补码,正数的补码等于其原码。
2加上了一串数字后再加1后等于0,那么那一串数字+1应该等于几,对,是-2。
所以-2的补码等于:2的原码形式全部按位取反再加+1,也就是负数的补码是其绝对值全部按位取反再+1。如果对反码有所了解,你应该能意识到这里负数的补码也等于其反码+1。
在完成了补码的设计后,我们就能够再计算机内使用加法电路完成将负数运算转变为加法运算的工作
我和谁相加会融为虚无的0,是我的反面(按位取反)和它带着的一点小小的融合剂(+1)
至此,结束。
如果你觉得这篇文章写的不错,多多点赞~收藏吧!