树的基本术语
一个节点包括一下内容
- 父节点的地址值
- 值
- 左节点的地址值
- 右节点的地址值
如果没有父节点或者没有左右节点,那么这些节点对应的位置是 null
常见术语
-
节点—树中的元素常称为节点
-
边—根和它的子树根(如果存在)之间形成边的边可到达另一个结点,则称这两个结点间存在一条路径。
-
双亲—若一个结点有子树,那么该结点称为子树根的双亲
-
孩子—子树的根是该结点的孩子
-
兄弟—有相同双亲的结点互为兄弟
-
后裔—一个结点的所有子树上的任何结点都是该结点的后裔
-
祖先—从根结点到某个结点路径上的所有结点都是该结点的祖先
-
度—一个结点拥有的子树数量称为该结点的度。度为 0 的结点称为叶子结点,树中结点的最大的度称为树的度
-
层次—一般将根节点的层次定义为 1, 其余节点的层次等于其双亲结点的层次加 1, 书中节点的最大层次称为该树的高度
-
无序树, 有序树, 如果一棵树中各结点的子树的次序不重要,可以交换位置,这样的树称为无序树。如果将树中结点的各棵子树看成是从左到右有次序的,则称该树为有序树。从左到右,可分别称这些子树为第一子树、第二子树等。
-
森林—森林是树的有限集合
左子树
- 对于任意一个节点 n,它的左子树是从根节点到 n 的路径上所有节点的集合,包括 n 自己。
右子树
- 对于任意一个节点 n,它的右子树是从根节点到 n 的路径上所有节点的集合,不包括 n 自己。
二叉查找树
左节点的值比父亲节点的值小
右节点的值比父亲节点的值大
我们经常使用这个二叉查找树来进行查找节点
二叉树的遍历方式
三种递归遍历
- 我们定义了二叉树的四种遍历运算,即先序遍历、中序通历、后序遍历和层次遍历。其中先序遍历、中序遍历和后序遍历的设计思想与二叉树的递归定义密切相关
层次遍历
- 层次遍历是利用二叉树中各结点所在的层次,按照从上到下、从左到右的顺序访问二叉树中的每一个结点。
先序, 中序, 后序遍历
-
对于这三种遍历方法而言, 遍历的逻辑是没有什么区别的, 唯一的区别在于, 什么时候输出
-
函数的递归调用, 就是函数的自身调用, 执行完之后会返回上一个被嵌套的函数, 去执行, 未执行的表达式
-
假设 L、V 和 R 分别代表遍历左子树、访问根结点和遍历右子树这三个操作,那么就可以得到六种遍历次序,分别是 VLR、LVR、LRV、VRL、RVL 和 RLV。
-
即先访问根结点的先序遍历 VLR、中间访问根结点的中序遍历 LVR 和最后访问根结点的后序遍历 LRV
三种遍历算法的总结
-
先序遍历算法读取的时候输出是在第一个,也就是说每次执行函数都会有输出,其是先从根节点开始的,然后遍历左子树,和右子树,所以它的结果一般是,从根节点开始输出,然后不断输出根节点的左子树内容,然后是到最下面的左子树结点的时候,判断有没有左右子树,没有的话,判断上一个有没有右子树,有的话先输出右子树,然后在继续判断有没有左子树,,,,
-
中序遍历算法输出在遍历左子树之后,到最下面一个左子树才开始输出,然后是判断其有没有右子树,没有的话,返回上一步,此时上一步的遍历左子树算法结束,然后输出结点,然后继续遍历右子树,如果是先序遍历的话,此时这个右子树会输出的,但是中序遍历却不会输出,而是继续判断这个右子树有没有左子树之后才会输出。这就是区别
-
后序遍历,就是先到最下方的一个左子树,然后是返回上一个节点,此时先序和中序,都会输出上面的结点,但是后序不会,后序的话,是只有子树输出完了,才会输出双亲结点
前序遍历从跟节点开始左子节点,右子节点的顺序遍历
当前,左,右的遍历方式
中序遍历我们先遍历最左边的节点(即最左边的叶子节点),等这个节点遍历完之后我们就往上一层,如果有右节点,那么先观察它有没有左节点,如果有的话那么我们就遍历左节点
记住关键点,一切都是以左节点为先
后序遍历
左,右,当前节点
层次遍历
一层一层的遍历
java 中常见的二叉树类型其实和 C 语言是类似的,并不是通过其特有的 LinkHashSet 还是 LinkArraylist,亦或者是 LinkHashMap, 本质上还是通过类来进行构建的
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
public class BinaryTree {
private TreeNode root;
public BinaryTree() {
this.root = null;
}
// 添加节点到二叉树
public void addNode(int val) {
root = addNodeRecursive(root, val);
}
// 递归方式添加节点到二叉树
private TreeNode addNodeRecursive(TreeNode current, int val) {
if (current == null) {
return new TreeNode(val);
}
if (val < current.val) {
current.left = addNodeRecursive(current.left, val);
} else if (val > current.val) {
current.right = addNodeRecursive(current.right, val);
}
return current;
}
// 遍历二叉树(示例为中序遍历)
public void traverse() {
traverseInOrder(root);
}
// 中序遍历二叉树
private void traverseInOrder(TreeNode node) {
if (node != null) {
traverseInOrder(node.left);
System.out.print(node.val + " ");
traverseInOrder(node.right);
}
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
// 添加节点
tree.addNode(50);
tree.addNode(30);
tree.addNode(20);
tree.addNode(40);
tree.addNode(70);
tree.addNode(60);
tree.addNode(80);
// 遍历二叉树
tree.traverse();
}
}
平衡二叉树
平衡二叉树的特点
二叉树左右两个子树的高度差不超过 1
任意节点的左右两个子树都是一颗平衡二叉树
平衡二叉树旋转
旋转触发时机
当添加一个节点之后, 该树不再是一颗平衡二叉树
左旋
就是将根节点的右侧往左拉, 原先的右子节点变成新的父节点, 并把多余的左子节点出让, 给已经降级的根节点当右子节点
从添加的节点开始,不断的往父节点中找不平衡的点


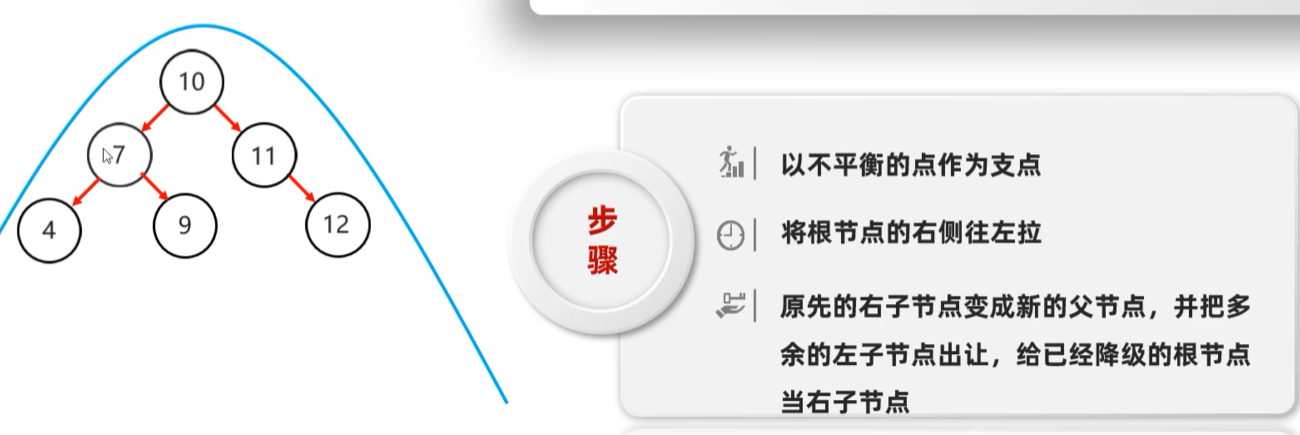
平衡右旋
右旋
就是将根节点的左侧往右拉, 左子节点变成了新的父节点, 并把多余的右子节点出让, 给已经降级根节点当左子节点
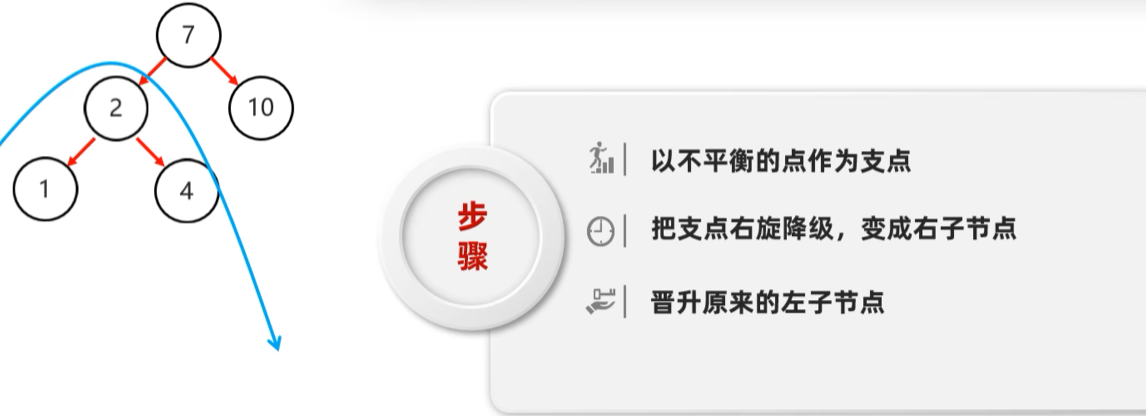
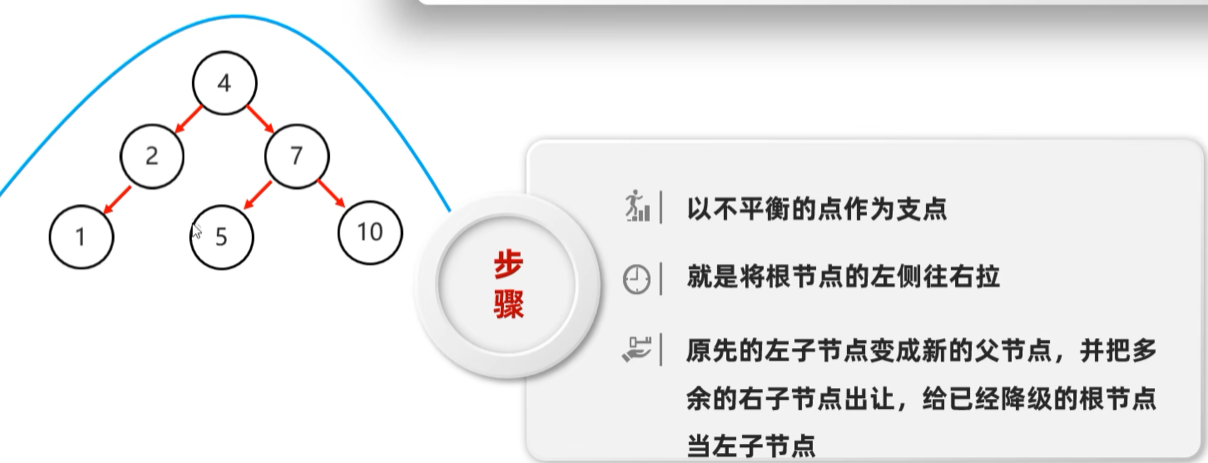
左右
左右: 当根节点左子树的右子树有节点插入, 导致二叉树不平衡
如何旋转: 先在左子树对应的节点位置进行左旋, 在对整体进行右旋

我们并不能通过一次旋转来实现这个二叉树的变换

红黑树


简单路径其实综合来说就是,不能回头
我们通过第五条规则来设定这个红色节点的数量
添加节点的规则
默认添加的节点是红色的,这样的话效率高
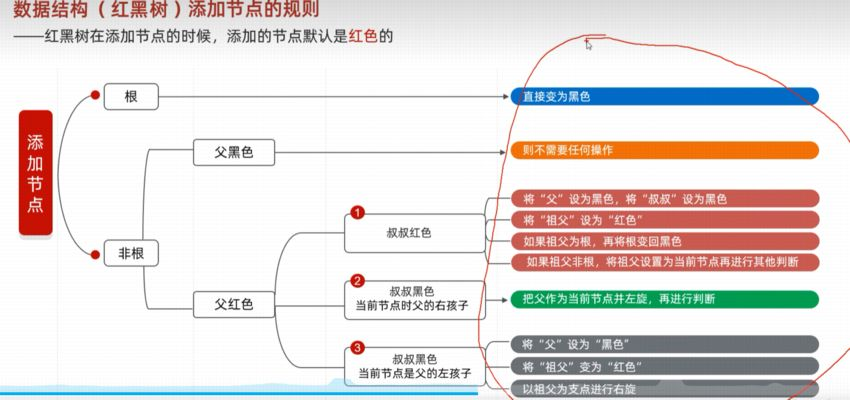
叔叔节点就是父节点的兄弟节点
根据这个操作来说,是不难的
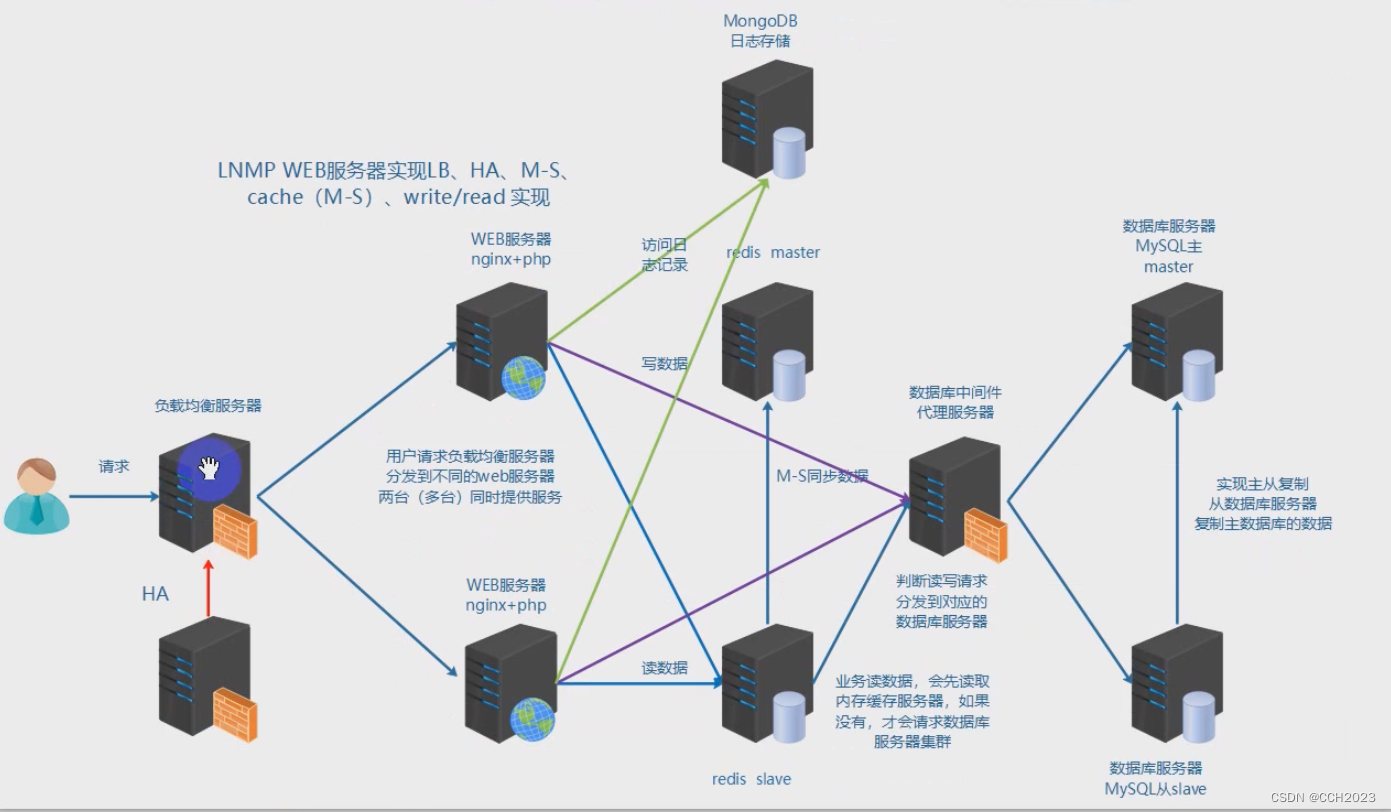
红黑树是一种增删改查数据性能相对都较好的结构






![[TQLCTF 2022]simple_bypass](https://img-blog.csdnimg.cn/b4a63438bf904e8e8edb978e8eaf0f92.png)