介绍

深度优先搜索（Depth-First Search，DFS）是一种常用的图搜索算法，它用于查找图或树数据结构中的路径或解决问题。下面是深度优先搜索的常见步骤以及一个示例问题：

深度优先搜索的常见步骤：

选择起始节点：首先，选择一个起始节点，从该节点开始搜索。
访问节点：访问当前节点，并标记它为已访问。这可以通过将节点标记为已访问或将其添加到访问过的节点列表中来实现。
探索相邻节点：从当前节点出发，探索其相邻节点。这可以通过遍历与当前节点相连接的边或邻接节点来实现。
递归或栈：对于每个相邻节点，如果它还没有被访问过，就递归地或使用栈将其作为当前节点进行访问。这是深度优先搜索的关键部分，它会一直沿着一个路径深入，直到达到叶子节点或无法继续深入为止。
回溯：当无法继续深入时，回溯到上一个节点，并尝试探索其他相邻节点，直到找到解决方案或访问完所有节点。
重复步骤3至步骤5：重复步骤3至步骤5，直到找到问题的解决方案或访问了所有可达节点。

简单的例子

#include <iostream>
#include <vector>

using namespace std;

// 定义图的节点结构
struct Node {
    int val;
    vector<Node*> neighbors;
    bool visited;

    Node(int _val) : val(_val), visited(false) {}
};

// 深度优先搜索函数
bool dfs(Node* current, Node* target, vector<Node*>& path) {
    if (current == target) {
        path.push_back(current);
        return true;
    }

    current->visited = true;
    path.push_back(current);

    for (Node* neighbor : current->neighbors) {
        if (!neighbor->visited) {
            if (dfs(neighbor, target, path)) {
                return true;
            }
        }
    }

    // 如果无法找到路径，回溯
    path.pop_back();
    return false;
}

int main() {
    // 创建节点
    Node* A = new Node(1);
    Node* B = new Node(2);
    Node* C = new Node(3);
    Node* D = new Node(4);

    // 构建图的连接关系
    A->neighbors.push_back(B);
    A->neighbors.push_back(C);
    B->neighbors.push_back(D);
    C->neighbors.push_back(D);

    // 初始化路径
    vector<Node*> path;

    // 执行深度优先搜索
    bool foundPath = dfs(A, D, path);

    // 输出结果
    if (foundPath) {
        cout << "Path from A to D found:" << endl;
        for (Node* node : path) {
            cout << node->val << " ";
        }
        cout << endl;
    } else {
        cout << "Path from A to D not found." << endl;
    }

    // 释放节点内存
    delete A;
    delete B;
    delete C;
    delete D;

    return 0;
}
/*
在这个示例中，我们首先定义了一个表示图节点的结构体Node，每个节点具有一个值、一个标记用于表示是否已访问和一个邻接节点的列表。然后，我们实现了一个深度优先搜索函数dfs，该函数递归地探索图中的节点，同时维护一个路径列表。如果找到从起始节点到目标节点的路径，它将返回true，并在路径列表中存储找到的路径。

在main函数中，我们创建了图的节点并构建了节点之间的连接关系。然后，我们调用dfs函数来查找从节点A到节点D的路径，并输出结果。如果路径存在，它将打印出路径上的节点值，否则会显示未找到路径。最后，我们释放了节点的内存以避免内存泄漏。
*/

题目1：华为机试题43 迷宫问题。

地址迷宫问题_牛客题霸_牛客网

题目描述：

定义一个二维数组 N*M ，如 5 × 5 数组下所示：

int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的路线。入口点为[0,0],既第一格是可以走的路。

数据范围：

2≤n,m≤10 ，输入的内容只包含

0≤val≤1

输入描述：

输入两个整数，分别表示二维数组的行数，列数。再输入相应的数组，其中的1表示墙壁，0表示可以走的路。数据保证有唯一解,不考虑有多解的情况，即迷宫只有一条通道。

输入：

5 5

0 1 0 0 0

0 1 1 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

复制

输出：

(0,0)

(1,0)

(2,0)

(2,1)

(2,2)

(2,3)

(2,4)

(3,4)

(4,4)

复制

示例2

输入：

5 5

0 1 0 0 0

0 1 0 1 0

0 0 0 0 1

0 1 1 1 0

0 0 0 0 0

复制

输出：

(0,0)

(1,0)

(2,0)

(3,0)

(4,0)

(4,1)

(4,2)

(4,3)

(4,4)

复制

说明：

注意：不能斜着走！！


#include <iostream>
#include<vector>
using namespace std;

vector<vector<int> > res;
bool dfs(vector<vector<int>>& v, int m, int n, int i, int j) {

    if (i == m - 1 && j == n - 1) {
        res.push_back({i, j});
        return true;
    }

    //通过这个false 判定这个结果。

    if (i < 0 || i >= m || j < 0 || j >= n || v[i][j] == -1 || v[i][j] == 1) {
        return false;
    }

    v[i][j] = -1;
    res.push_back({i, j});

    if (dfs(v, m, n, i - 1, j) || dfs(v, m, n, i + 1, j) ||
            dfs(v, m, n, i, j - 1) || dfs(v, m, n, i, j + 1)) {
        return true;
    }

    res.pop_back();
    v[i][j] = 0;

    return false;

}

int main() {

    int m, n;
    int temp;
    cin >> m >> n;
    vector<vector<int> > v(m, vector<int>(n, 0));

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {

            cin >> v[i][j];
        }
    }

    dfs(v,m,n,0,0);

    for(const auto & x:res){
        // printf("(%d,%d)\n",x[0],[1]);
        // printf("(%d,%d) \n",x[0],[1]);
        printf("(%d,%d)\n", x[0], x[1]);
    }

    return 0;

}

题目2：剑指offer12 矩阵中的路径

链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

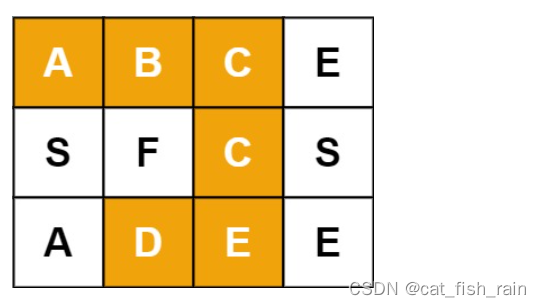
例如，在下面的 3×4 的矩阵中包含单词 "ABCCED"（单词中的字母已标出）。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

class Solution6 {
public:
       bool dfs(vector<vector<char>>& board,string word,int i,int j,int k,vector<vector<int>> &path){

        if(i<0||i>=board.size()||j<0||j>=board[0].size()||path[i][j]==1){
            return false;
        }

          if(board[i][j]==word[k]&&k==word.size()-1){
            return true;
        }

        if(word[k]==board[i][j]){

            path[i][j]=1;
            if(dfs(board,word,i+1,j,k+1,path)||dfs(board,word,i-1,j,k+1,path)||dfs(board,word,i,j-1,k+1,path)||dfs(board,word,i,j+1,k+1,path)){
                 return true;
        }

        }

        path[i][j]=0;
        return false;

    }

    bool exist(vector<vector<char>>& board, string word) {

        int m=board.size();
        int n=board[0].size();
        bool res=false;
        vector<vector<int> > path(m,vector<int>(n,0));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){

                res = dfs(board, word, i, j, 0, path);
                if(res){
                    //i,j 是起点只要有一个七点满足条件就可以
                    return true;
                }

            }
        }

        return  res;
    }

};

int main()
{

    Solution6 s;
    vector<vector<char>> board = {{'A', 'B', 'C', 'E'}, {'S', 'F', 'C', 'S'}, {'A', 'D', 'E', 'E'}};
    // vector< vector<char> > board={}
    string word = "ABCCED";

    bool res = s.exist(board, word);
    cout << res << endl;

    system("pause");
    return 0;
}

题目3 leetcode 200岛屿的数量

leet200 岛屿的数量 https://leetcode.cn/problems/number-of-islands/

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [

["1","1","1","1","0"],

["1","1","0","1","0"],

["1","1","0","0","0"],

["0","0","0","0","0"]

]

输出：1

示例 2：

输入：grid = [

["1","1","0","0","0"],

["1","1","0","0","0"],

["0","0","1","0","0"],

["0","0","0","1","1"]

]

//可以这么理解，(遍历整个岛屿的元素，如果是1就对这个点的值进行深度优先搜索，将相邻的全部改成0) 岛屿的数量+1。

class Solution7
{
public:
    int n;
    void dfs(vector<vector<char>> &grid, int i, int j, int m, int n)
    {

        if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0')
        {
            return;
        }

        grid[i][j] = '0';
        dfs(grid, i - 1, j, m, n);
        dfs(grid, i + 1, j, m, n);
        dfs(grid, i, j - 1, m, n);
        dfs(grid, i, j + 1, m, n);

        return;
    }

    int numIslands(vector<vector<char>> &grid)
    {

        int m = grid.size();
        int n = grid[0].size();

        int num = 0;
        // vector<vector<bool> > path=vector(m,vector<int>(n,0));

        for (int i = 0; i < m; i++)
        {

            for (int j = 0; j < n; j++)
            {

                if (grid[i][j] == '1')
                {
                    n++;
                    dfs(grid, i, j, m, n);
                }
            }
        }

        return n;
    }
};

int main()
{

    Solution7 s7;

    vector<vector<char>> gird = {{'1'}, {'1'}};

    auto res = s7.numIslands(gird);
    cout << res << endl;

    system("pause");
    return 0;
}

=================================后续待补=================================