一，引导简介
简单的来看三分法实际就是二分法的另一种扩展，可以完全的看成二分法，我们介绍几个特殊的点，才能使用这个解法来进行相关的算法求解：求解单调性改变的点，在本个区间中只有一个导数为 0 的点，使用下面的模板进行求解即可。

三分法是一种用于在有序数组或函数上进行搜索的算法，其主要思想是将搜索空间分成三个部分，而不是传统的二分法（将搜索空间分为两半）。这可以在某些情况下更快地找到目标值。

下面是三分法的基本工作原理和步骤：

1. 确定搜索范围： 首先，你需要确定搜索的范围。这通常是一个有序数组或一个连续的函数区间。

2. 将搜索范围分成三等分： 与二分法不同，三分法将搜索范围分成三个部分，而不是两个。你需要找到两个分隔点，将搜索范围划分为三个部分。这两个分隔点通常距离搜索范围的两端相等距离。

3. 比较中点： 计算并比较中点1和中点2处的函数值或数组元素值。根据比较的结果，你可以确定目标值位于哪个部分：左侧、中间还是右侧。

4. 更新搜索范围： 根据上一步的比较结果，你可以缩小搜索范围。如果目标值在左侧部分，将搜索范围更新为左半部分；如果在右侧，将搜索范围更新为右半部分；如果在中间，你已经找到了目标值。

5. 重复步骤： 重复步骤2至4，直到找到目标值或搜索范围足够小。

三分法的主要优点是，在某些情况下，它可以比二分法更快地找到目标值，因为它在每一步将搜索范围缩小为三分之一，而不是一半。这对于某些特定的函数或问题非常有效，但并不适用于所有情况。

需要注意的是，三分法通常用于连续函数的优化问题，以寻找函数的最大值或最小值，而不仅仅是查找特定值。在算法竞赛中，你可能会遇到需要使用三分法的问题，尤其是涉及到优化的情况。

二，算法重现

/*
    1.算法 ： 三分法
    2.算法思想 ： 三分法使用二分法的主要框架,并且通过单导数为零的函数特性进行的修改
    3.算法实现 ： 整个框架和二分法一致 , check() 函数函数的写法可以自行模拟 , 
    一般情况下 我们对比较小的函数进行操作 。
*/


#include <iostream>
#define eps 0.000001 
using namespace std ;

const int N = 20 ; 

double q[N] ; 

int n ;

double l , r ;

bool check()
{

}

int main ()
{
    cin >> n >> l >> r ;
    for(int i = n ; i >= 0 ; i -- )
        cin >> q[i] ; 
    while ( r - l >  eps )
    {
        double mid1 = (r - l ) * ( 1.0 / 3) + l ;
        double mid2 = (r - l )* (2.0 / 3) + l ;
      
        if(check())    r = mid2 ;
        else l = mid1 ; 
    }
    // 主要操作 。
    cout << l << endl ;
    return 0 ; 
}

三，在线解题

题目来源洛谷，仅作学习使用，侵权请联系删除

【模板】三分法

题目描述

如题，给出一个 $N$ 次函数，保证在范围 $[l,r]$ 内存在一点 $x$，使得 $[l,x]$ 上单调增，$[x,r]$ 上单调减。试求出 $x$ 的值。

输入格式

第一行一次包含一个正整数 $N$ 和两个实数 $l,r$，含义如题目描述所示。

第二行包含 $N+1$ 个实数，从高到低依次表示该 $N$ 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 $x$ 的值。若你的答案与标准答案的相对或绝对误差不超过 $10^{-5}$ 则算正确。

样例 #1

样例输入 #1

3 -0.9981 0.5
1 -3 -3 1

样例输出 #1

-0.41421

提示

对于 $100\%$ 的数据，$6\le N\le 13$，函数系数均在 $[-100,100]$ 内且至多 $15$ 位小数，$|l|,|r|\le 10$ 且至多 $15$ 位小数。$l\le r$。

【样例解释】

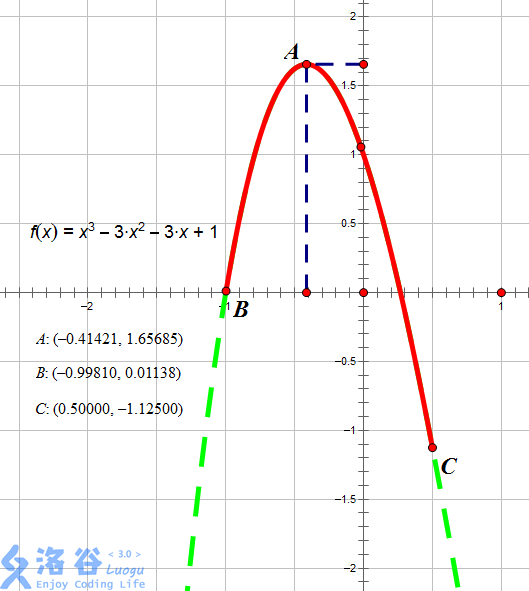
如图所示，红色段即为该函数 $f(x)=x^3-3x^2-3x+1$ 在区间 $[-0.9981,0.5]$ 上的图像。

当 $x=-0.41421$ 时图像位于最高点，故此时函数在 $[l,x]$ 上单调增，$[x,r]$ 上单调减，故 $x=-0.41421$，输出 $-0.41421$。

    #include <iostream>
    #define eps 0.000001 
    using namespace std ;

    const int N = 20 ; 

    double q[N] ; 

    int n ;

    double l , r ;

    double f(double x )
    {
        double sum = 0 ;
        for(int i = 0 ; i <= n ; i ++ )
        {
         
            double ans = q[i] ;
            for(int j = 0 ; j < i ; j ++ )
            {
                ans *= x ;
            }
            sum += ans ;
        }
        
        return sum ;
    }

    int main ()
    {
        cin >> n >> l >> r ;
        for(int i = n ; i >= 0 ; i -- )
            cin >> q[i] ; 
        while ( r - l >  eps )
        {
            double mid1 = (r - l ) * ( 1.0 / 3) + l ;
            double mid2 = (r - l )* (2.0 / 3) + l ;
          
            if(f(mid2) < f(mid1) )    r = mid2 ;
            else l = mid1 ; 

        }
        cout << l << endl ;
        return 0 ; 
    }