题目：

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例：

题目链接：647. 回文子串 - 力扣（LeetCode）

解法：

什么是回文字符串：字符串关于中心位置是对称的。

动规五部曲：

1确定dp数组以及下标的含义

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

2.确定递推公式

在确定递推公式时，就要分析如下几种情况。

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

• 情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
• 情况二：下标i 与 j相差为1，例如aa，也是回文子串
• 情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

以上三种情况分析完了，那么递归公式如下：

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

result就是统计回文子串的数量。

注意这里我没有列出当s[i]与s[j]不相等的时候，因为在下面dp[i][j]初始化的时候，就初始为false。

3.dp数组如何初始化

dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹配上了。

所以dp[i][j]初始化为false。

4.确定遍历顺序

遍历顺序可有有点讲究了。

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。

dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

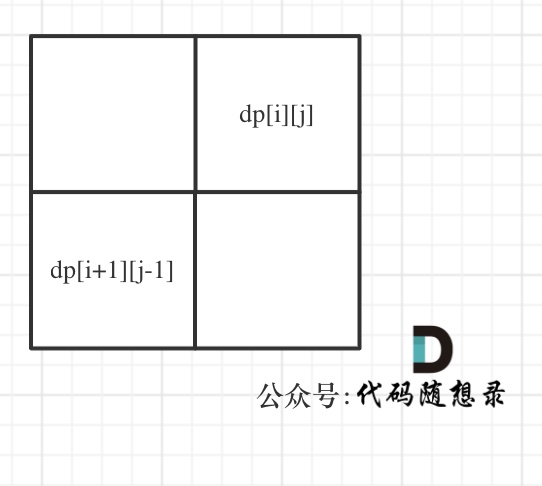
如果这矩阵是从上到下，从左到右遍历，那么会用到没有计算过的dp[i + 1][j - 1]，也就是根据不确定是不是回文的区间[i+1,j-1]，来判断了[i,j]是不是回文，那结果一定是不对的。

所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

有的代码实现是优先遍历列，然后遍历行，其实也是一个道理，都是为了保证dp[i + 1][j - 1]都是经过计算的。

5.举例推导dp数组：略

class Solution {
public:
    int countSubstrings(string s) 
    {
        int result=0;
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        for (int i = s.size() - 1; i >= 0; i--) 
        {  // 注意遍历顺序
            for (int j = i; j < s.size(); j++) 
            {
                if (s[i] == s[j]) 
                {
                    if (j - i <= 1) 
                    { // 情况一 和 情况二
                        result++;
                        dp[i][j] = true;
                    } 
                    else if ((j - i > 1)&&dp[i + 1][j - 1]==true) 
                    { // 情况三
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
};