文章目录

🍀堆的插入与删除
- 🛫堆的插入
- - 🚩代码实现：
- 🛬堆的删除
🎋堆的常见习题
- 🎈习题一
- 🎈习题二
- 🎈习题三
🎄PriorityQueue
- 🐱‍👓PriorityQueue的特性
🎍PriorityQueue常用接口介绍
- 🛫优先级队列的构造
- - 🚨注意：
- 🛬插入/删除/获取优先级最高的元素
- 🎡PriorityQueue的扩容方式
🌲PriorityQueue面试题---[最小K个数](https://leetcode.cn/problems/smallest-k-lcci/submissions/)
- 🐱‍👤题目描述：
- 🐱‍🐉示例与提示：
- 🐱‍👓思路解析：
- 🐱‍🏍代码实现：
- 🚨注意：
🌳堆的应用
- 🐱‍👤PriorityQueue的实现
- 🐱‍🐉堆排序
😎拓展（java对象的比较）：
- 🧭基于Comparble接口类的比较
- - 📌基于比较器比较
  - 📌三种方式对比
  - 📌集合框架中PriorityQueue的比较方式
🐱‍👓top-k问题
- - 📌代码实现：
⭕总结

🍀堆的插入与删除

🛫堆的插入

堆的插入总共需要两个步骤：

先将元素放入到底层空间中(注意：空间不够时需要扩容)
将最后新插入的节点向上调整，直到满足堆的性质

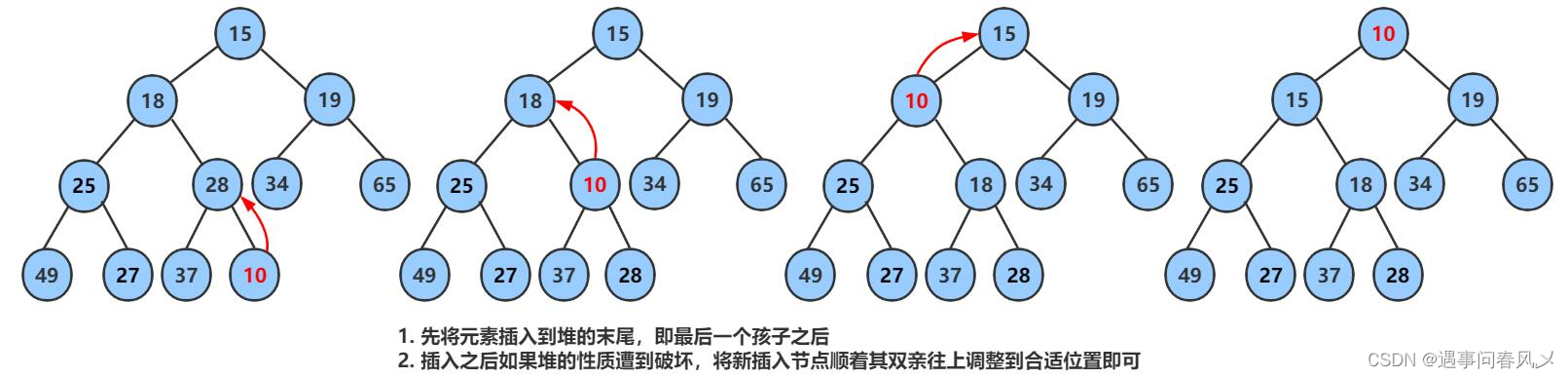
在这里插入图片描述

🚩代码实现：

public class MyHeap {
    public void shiftUp(int child,int[] array) {
// 找到child的双亲
        int parent = (child - 1) / 2;
        while (child > 0) {
// 如果双亲比孩子大，parent满足堆的性质，调整结束
            if (array[parent] > array[child]) {
                break;
            } 
            else{
// 将双亲与孩子节点进行交换
                int t = array[parent];
                array[parent] = array[child];
                array[child] = t;
// 小的元素向下移动，可能到值子树不满足对的性质，因此需要继续向上调增
                child = parent;
                parent = (child - 1) / 1;
            }
        }
    }
}

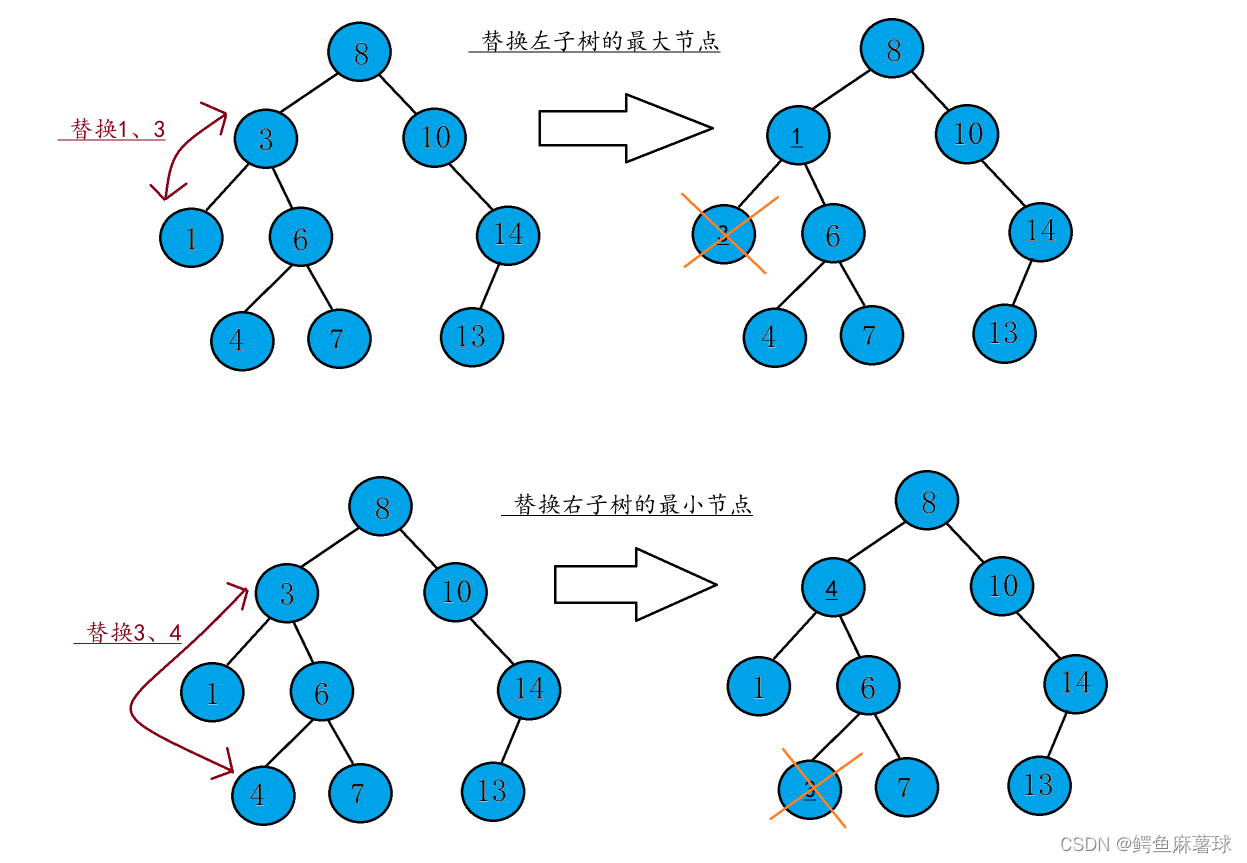
🛬堆的删除

注意：堆的删除一定删除的是堆顶元素。具体如下：

将堆顶元素对堆中最后一个元素交换
将堆中有效数据个数减少一个
对堆顶元素进行向下调整

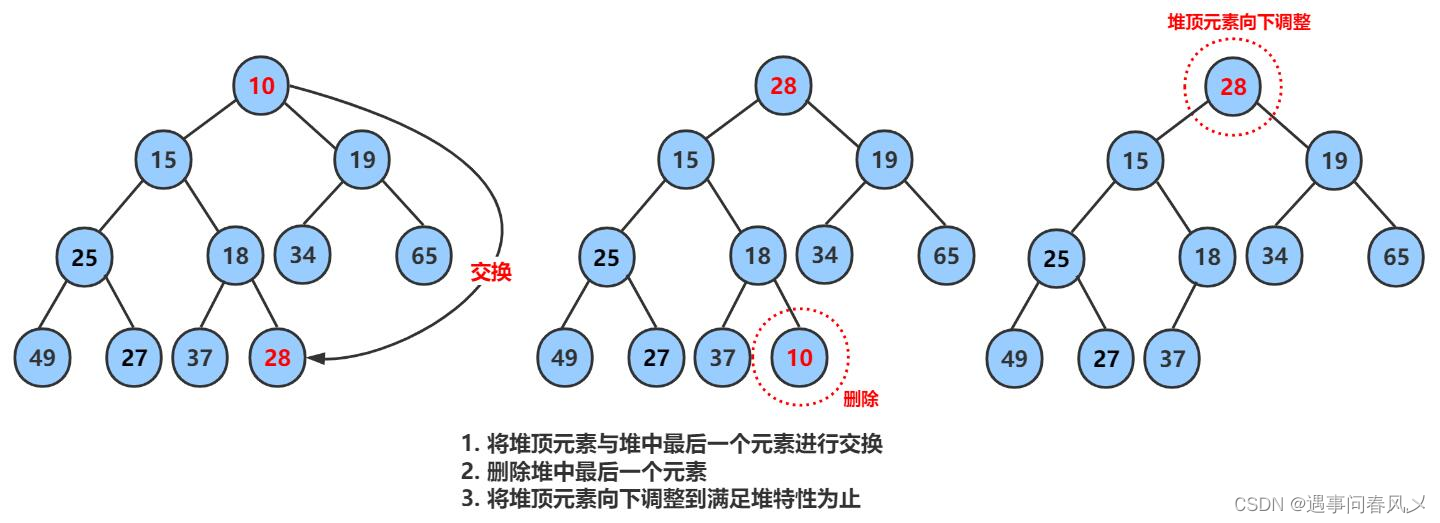
在这里插入图片描述
结合前面博主讲的向下调整代码，这个代码实现就很简单了，这里博主就不展示实现了

🎋堆的常见习题

🎈习题一

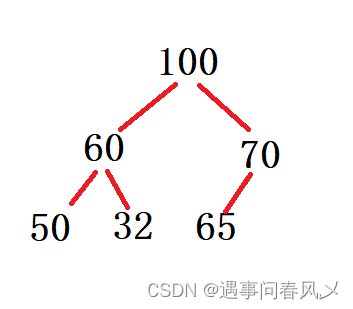
下列关键字序列为堆的是:(A)
A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60
D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 F: 50,100,70,65,60,32

解析：
通过画图，很容易得到A选项是对的

🎈习题二

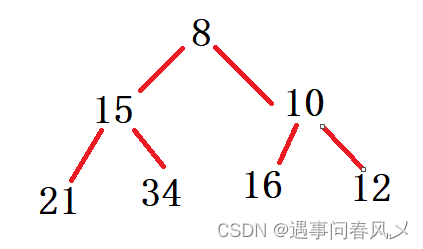
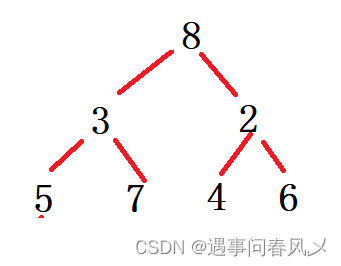
.已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是(C)

A: 1 B: 2 C: 3 D: 4

解析：
小根堆如下：

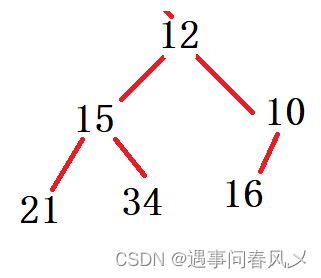
删除8后

比较情况：

15与10比较
10与12比较
12与16比较

所以对比次数为三次，答案为C

🎈习题三

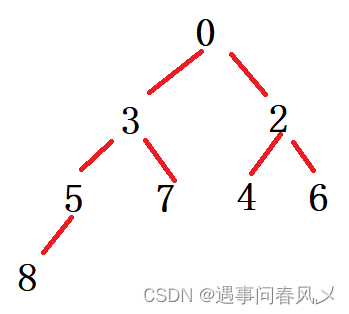
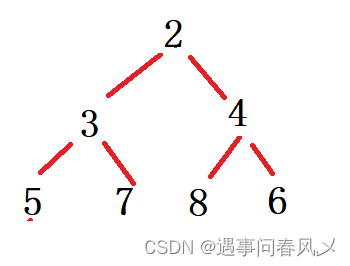
最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是(C)
A: [3，2，5，7，4，6，8] B: [2，3，5，7，4，6，8]
C: [2，3，4，5，7，8，6] D: [2，3，4，5，6，7，8]

解析：
小根堆如下：

删除堆顶元素0后为

接下来向下调整

所以答案选C

🎄PriorityQueue

🐱‍👓PriorityQueue的特性

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue
在这里插入图片描述
关于PriorityQueue的使用要注意：

使用时必须导入PriorityQueue所在的包，即：

import java.util.PriorityQueue;

PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出
ClassCastException异常
不能插入null对象，否则会抛出NullPointerException
没有容量限制，可以插入任意多个元素，其内部可以自动扩容
插入和删除元素的时间复杂度为
PriorityQueue底层使用了堆数据结构
PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素

🎍PriorityQueue常用接口介绍

🛫优先级队列的构造

此处只是列出了PriorityQueue中常见的几种构造方式。
在这里插入图片描述

    static void TestPriorityQueue(){
// 创建一个空的优先级队列，底层默认容量是11
        PriorityQueue<Integer> q1 = new PriorityQueue<>();
// 创建一个空的优先级队列，底层的容量为initialCapacity
        PriorityQueue<Integer> q2 = new PriorityQueue<>(100);
        ArrayList<Integer> list = new ArrayList<>();
        list.add(4);
        list.add(3);
        list.add(2);
        list.add(1);
// 用ArrayList对象来构造一个优先级队列的对象
// q3中已经包含了三个元素
        PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
        System.out.println(q3.size());
        System.out.println(q3.peek());
    }

🚨注意：

默认情况下，PriorityQueue队列是小堆，如果需要大堆需要用户提供比较器

import java.util.Comparator;
import java.util.PriorityQueue;

// 用户自己定义的比较器：直接实现Comparator接口，然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
}
public class TestPriorityQueue {
    public static void main(String[] args) {
        PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());
        p.offer(4);
        p.offer(3);
        p.offer(2);
        p.offer(1);
        p.offer(5);
        System.out.println(p.peek());
    }
}

🛬插入/删除/获取优先级最高的元素

在这里插入图片描述
测试代码如下：

    static void TestPriorityQueue2(){
        int[] arr = {4,1,9,2,8,0,7,3,6,5};
// 一般在创建优先级队列对象时，如果知道元素个数，建议就直接将底层容量给好
// 否则在插入时需要不多的扩容
// 扩容机制：开辟更大的空间，拷贝元素，这样效率会比较低
        PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);
        for (int e: arr) {
            q.offer(e);
        }
        System.out.println(q.size()); // 打印优先级队列中有效元素个数
        System.out.println(q.peek()); // 获取优先级最高的元素
// 从优先级队列中删除两个元素之和，再次获取优先级最高的元素
        q.poll();
        q.poll();
        System.out.println(q.size()); // 打印优先级队列中有效元素个数
        System.out.println(q.peek()); // 获取优先级最高的元素
        q.offer(0);
        System.out.println(q.peek()); // 获取优先级最高的元素
// 将优先级队列中的有效元素删除掉，检测其是否为空
        q.clear();
        if(q.isEmpty()){
            System.out.println("优先级队列已经为空!!!");
        } else {
            System.out.println("优先级队列不为空");
        }
    }

🎡PriorityQueue的扩容方式

以下是JDK 1.8中，PriorityQueue的扩容方式：

    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
// Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                (oldCapacity + 2) :
                (oldCapacity >> 1));
// overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }
    private static int hugeCapacity(int minCapacity) {
        if (minCapacity < 0) // overflow
            throw new OutOfMemoryError();
        return (minCapacity > MAX_ARRAY_SIZE) ?
                Integer.MAX_VALUE :
                MAX_ARRAY_SIZE;
    }

优先级队列的扩容说明：

如果容量小于64时，是按照oldCapacity的2倍方式扩容的
如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容

🌲PriorityQueue面试题—最小K个数

🐱‍👤题目描述：

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

🐱‍🐉示例与提示：

在这里插入图片描述

🐱‍👓思路解析：

我们只需要将该数组建堆

然后利用堆的性质输出前k个元素就行

🐱‍🏍代码实现：

class Solution {
    public int[] smallestK(int[] arr, int k) {
        if(null == arr || k <= 0)
            return new int[0];
        PriorityQueue<Integer> q1 = new PriorityQueue<>();
        for(int i = 0; i < arr.length; i ++) {
            q1.offer(arr[i]);
        }
        int[] elem = new int[k];
        for(int i = 0; i < k; i ++) {
            if(!q1.isEmpty()) {
            elem[i] = q1.poll();
            } else {
                break;
            }
            
        }
        return elem;
    }
}

🚨注意：

该解法只是PriorityQueue的简单使用，并不是topK最好的做法

那topk该如何实现？下面介绍

🌳堆的应用

🐱‍👤PriorityQueue的实现

用堆作为底层结构封装优先级队列

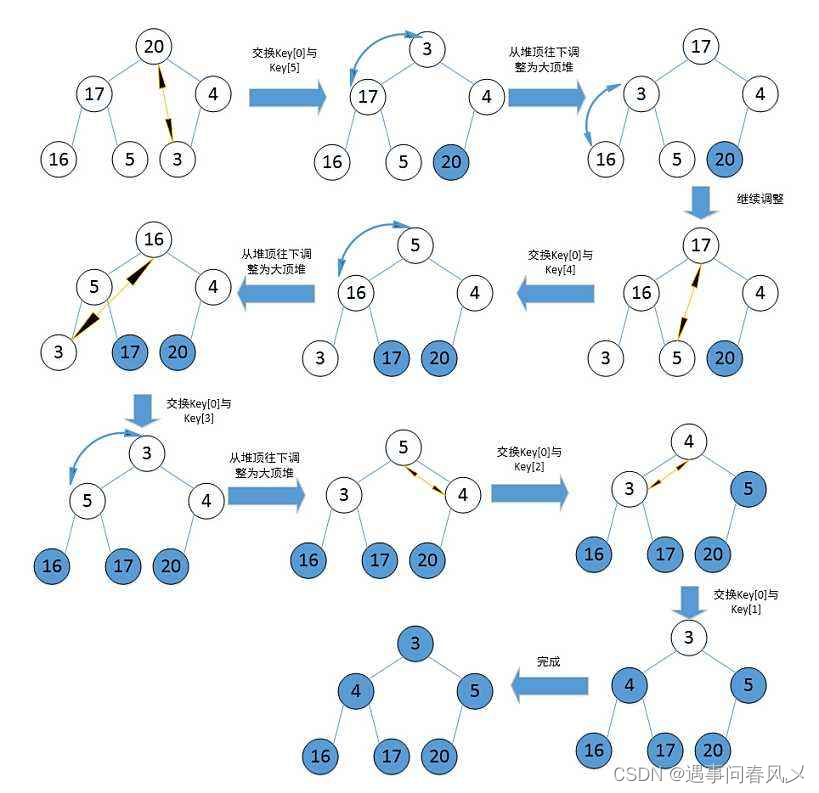
🐱‍🐉堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤

建堆

升序：建大堆
降序：建小堆

利用堆删除思想来进行排序

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
在这里插入图片描述

😎拓展（java对象的比较）：

🧭基于Comparble接口类的比较

Comparble是JDK提供的泛型的比较接口类，源码实现具体如下：

public interface Comparable<E> {
    // 返回值:
    // < 0: 表示 this 指向的对象小于 o 指向的对象
    // == 0: 表示 this 指向的对象等于 o 指向的对象
    // > 0: 表示 this 指向的对象大于 o 指向的对象
    int compareTo(E o);
}

对用用户自定义类型，如果要想按照大小与方式进行比较时：在定义类时，实现Comparble接口即可，然后在类中重写compareTo方法

例如以下代码：

public class Card implements Comparable<Card> {
    public int rank; // 数值
    public String suit; // 花色
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }
    // 根据数值比较，不管花色
    // 这里我们认为 null 是最小的
    @Override
    public int compareTo(Card o) {
        if (o == null) {
            return 1;
        }
        return rank - o.rank;
    }
    public static void main(String[] args){
        Card p = new Card(1, "♠");
        Card q = new Card(2, "♠");
        Card o = new Card(1, "♠");
        System.out.println(p.compareTo(o)); // == 0，表示牌相等
        System.out.println(p.compareTo(q)); // < 0，表示 p 比较小
        System.out.println(q.compareTo(p)); // > 0，表示 q 比较大
    }
}

📌基于比较器比较

按照比较器方式进行比较，具体步骤如下：

用户自定义比较器类，实现Comparator接口

public interface Comparator<T> {
    // 返回值:
// < 0: 表示 o1 指向的对象小于 o2 指向的对象
// == 0: 表示 o1 指向的对象等于 o2 指向的对象
// > 0: 表示 o1 指向的对象等于 o2 指向的对象
    int compare(T o1, T o2);
}

注意：区分Comparable和Comparator

覆写Comparator中的compare方法

import java.util.Comparator;
class Card {
    public int rank; // 数值
    public String suit; // 花色
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }
}
public class CardComparator implements Comparator<Card> {
    
    // 根据数值比较，不管花色
// 这里我们认为 null 是最小的
    @Override
    public int compare(Card o1, Card o2) {
        if (o1 == o2) {
            return 0;
        } if
        (o1 == null) {
            return -1;
        }
        if (o2 == null) {
            return 1;
        } 
        return o1.rank - o2.rank;
    }
    public static void main(String[] args){
        Card p = new Card(1, "♠");
        Card q = new Card(2, "♠");
        Card o = new Card(1, "♠");
// 定义比较器对象
        CardComparator cmptor = new CardComparator();
// 使用比较器对象进行比较
        System.out.println(cmptor.compare(p, o)); // == 0，表示牌相等
        System.out.println(cmptor.compare(p, q)); // < 0，表示 p 比较小
        System.out.println(cmptor.compare(q, p)); // > 0，表示 q 比较大
    }
}

注意：Comparator是java.util 包中的泛型接口类，使用时必须导入对应的包

📌三种方式对比

在这里插入图片描述

📌集合框架中PriorityQueue的比较方式

集合框架中的PriorityQueue底层使用堆结构，因此其内部的元素必须要能够比大小，PriorityQueue采用了：
Comparble和Comparator两种方式。

Comparble是默认的内部比较方式，如果用户插入自定义类型对象时，该类对象必须要实现Comparble接口，并覆写compareTo方法
用户也可以选择使用比较器对象，如果用户插入自定义类型对象时，必须要提供一个比较器类，让该类实现Comparator接口并覆写compare方法。

// JDK中PriorityQueue的实现：
public class PriorityQueue<E> extends AbstractQueue<E>
        implements java.io.Serializable {
    // ...
    // 默认容量
    private static final int DEFAULT_INITIAL_CAPACITY = 11;
    // 内部定义的比较器对象，用来接收用户实例化PriorityQueue对象时提供的比较器对象
    private final Comparator<? super E> comparator;
    // 用户如果没有提供比较器对象，使用默认的内部比较，将comparator置为null
    public PriorityQueue() {
        this(DEFAULT_INITIAL_CAPACITY, null);
    } 
    // 如果用户提供了比较器，采用用户提供的比较器进行比较
    public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
    // Note: This restriction of at least one is not actually needed,
    // but continues for 1.5 compatibility
        if (initialCapacity < 1)
            throw new IllegalArgumentException();
        this.queue = new Object[initialCapacity];
        this.comparator = comparator;
    } 
    // ...
    // 向上调整：
    // 如果用户没有提供比较器对象，采用Comparable进行比较
    // 否则使用用户提供的比较器对象进行比较
    private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }
    // 使用Comparable
    @SuppressWarnings("unchecked")
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    } 
    // 使用用户提供的比较器对象进行比较
    @SuppressWarnings("unchecked")
    private void siftUpUsingComparator(int k, E x) {
        }while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

🐱‍👓top-k问题

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序

但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

用数据集合中前K个元素来建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

🚨将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素🚨

📌代码实现：

import java.util.Comparator;
import java.util.PriorityQueue;

class GreaterIntComp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2 - o1;
    }
}
class Solution {
    public int[] smallestK(int[] arr, int k) {
        if(null == arr || k <= 0)
            if(k <= 0) {
                return new int[k];
            }
        GreaterIntComp greaterCmp = new GreaterIntComp();
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(greaterCmp);
		//先将前K个元素，创建大根堆
        for(int i = 0; i < k; i++) {
            maxHeap.offer(arr[i]);
        }
        //从第K+1个元素开始，每次和堆顶元素比较
        for (int i = k; i < arr.length; i++) {
            int top = maxHeap.peek();
            if(arr[i] < top) {
                maxHeap.poll();
                maxHeap.offer(arr[i]);
            }
        }
	//取出前K个
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            int val = maxHeap.poll();
            ret[i] = val;
        }
        return ret;
    }
}