目录

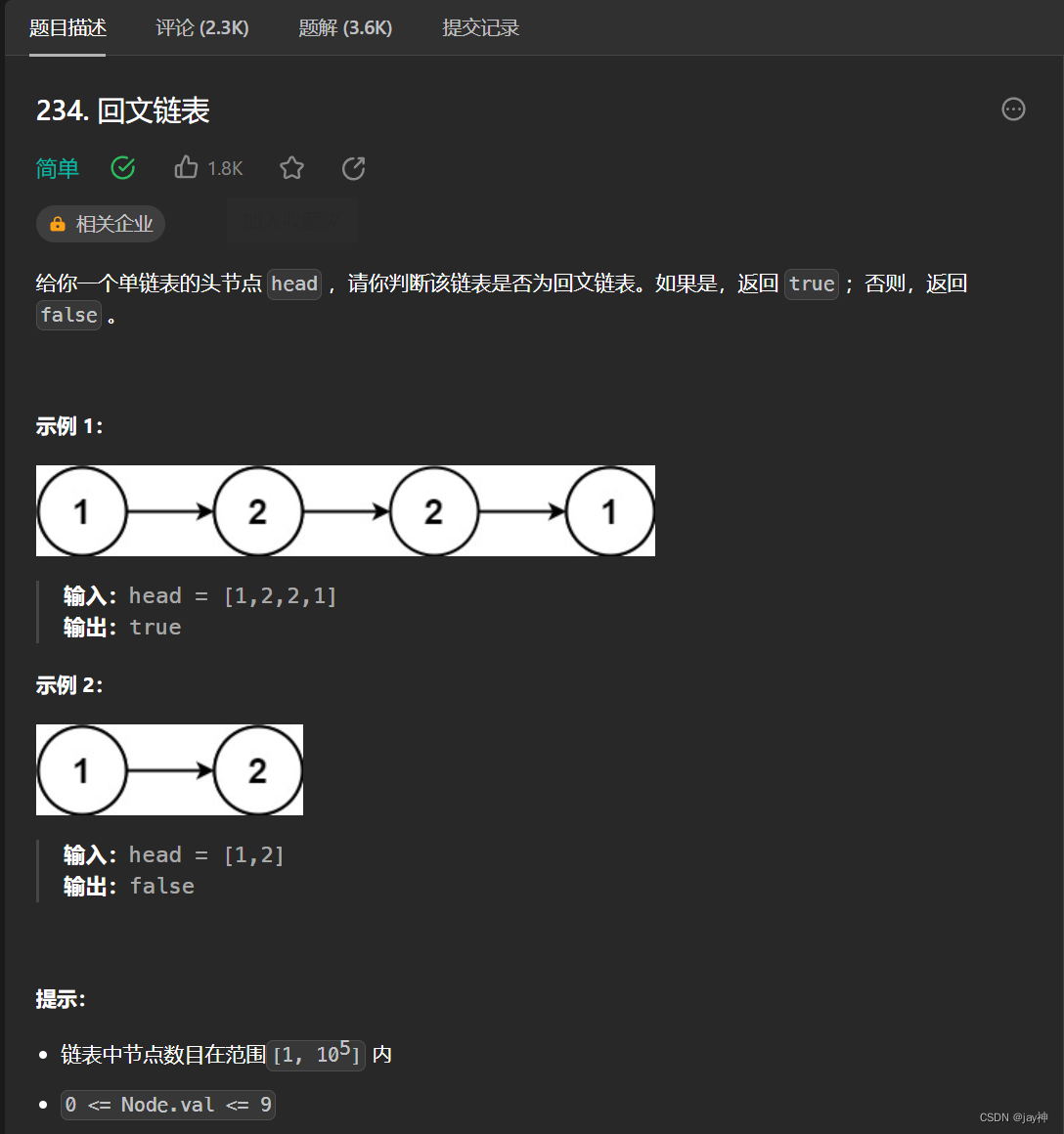
题目：

示例：

分析：

代码：

---

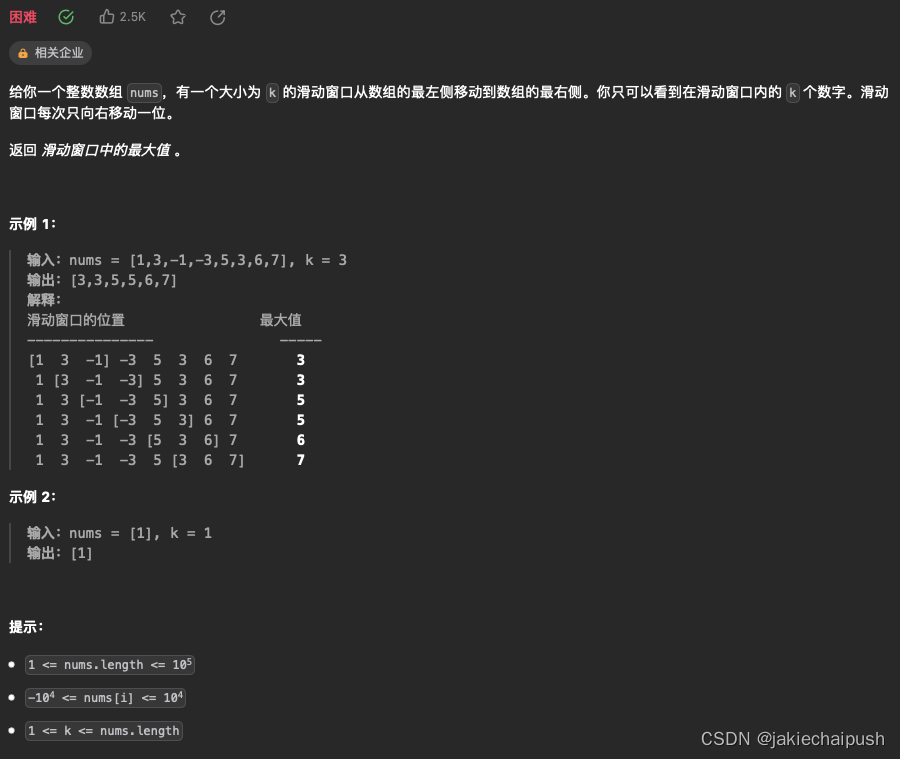
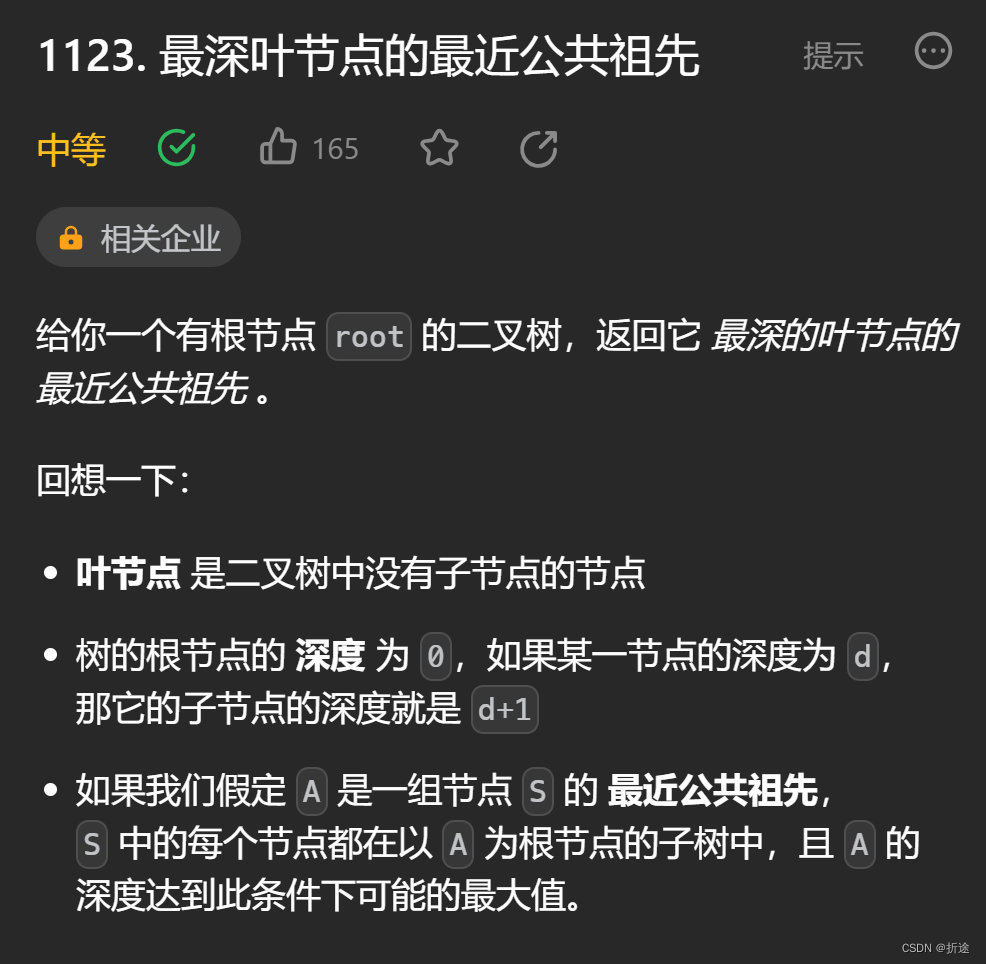
题目：

示例：

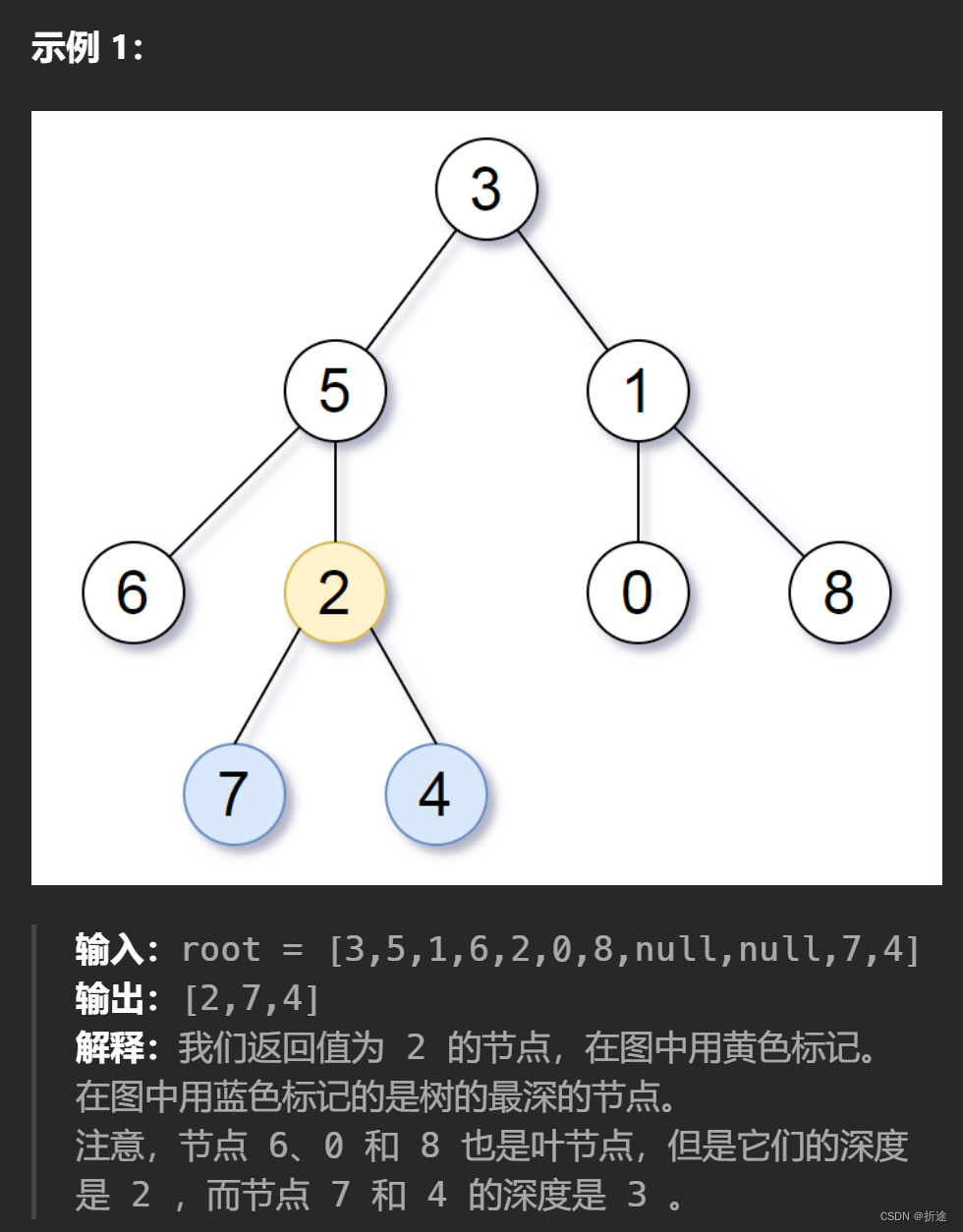
分析：

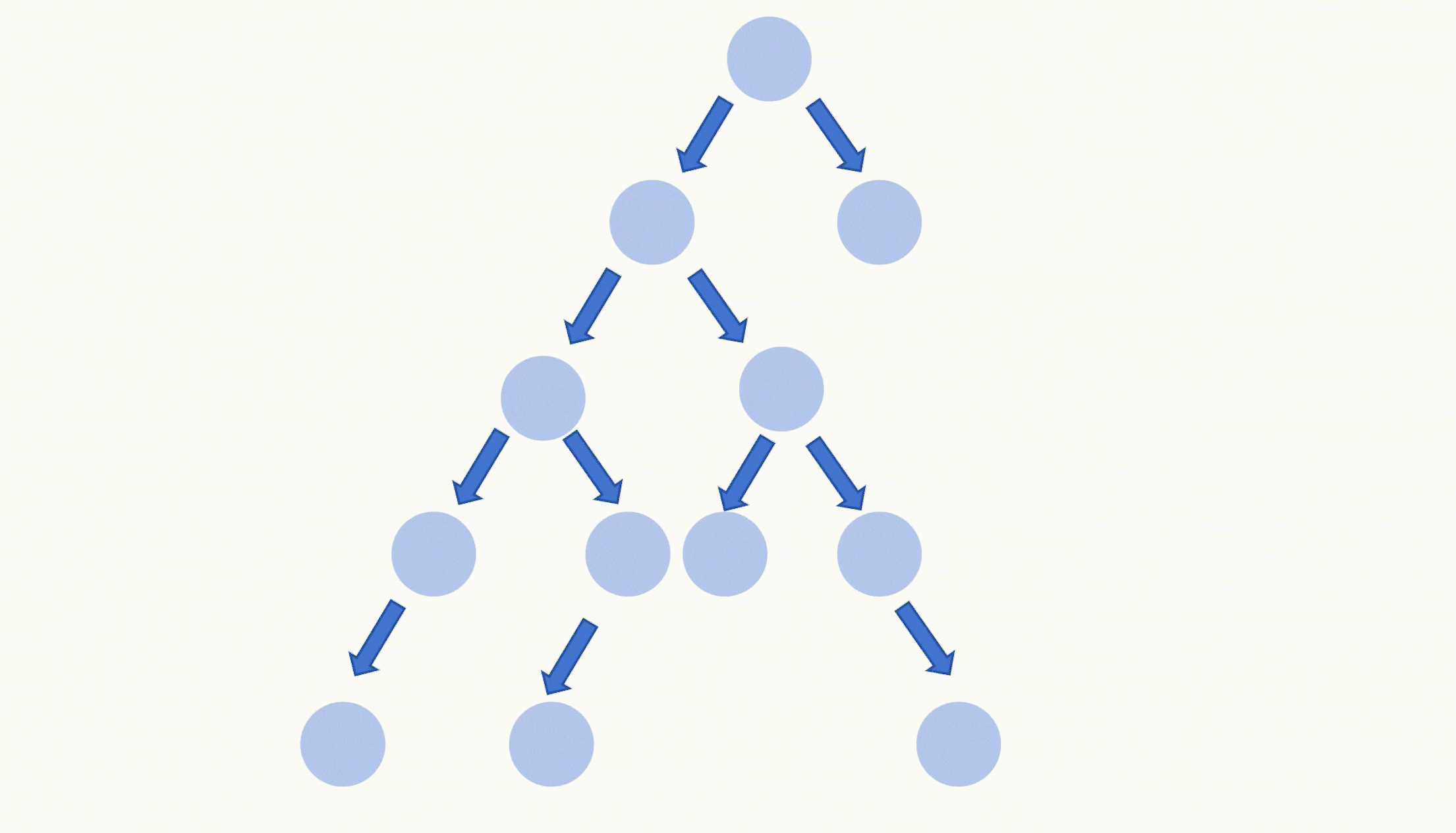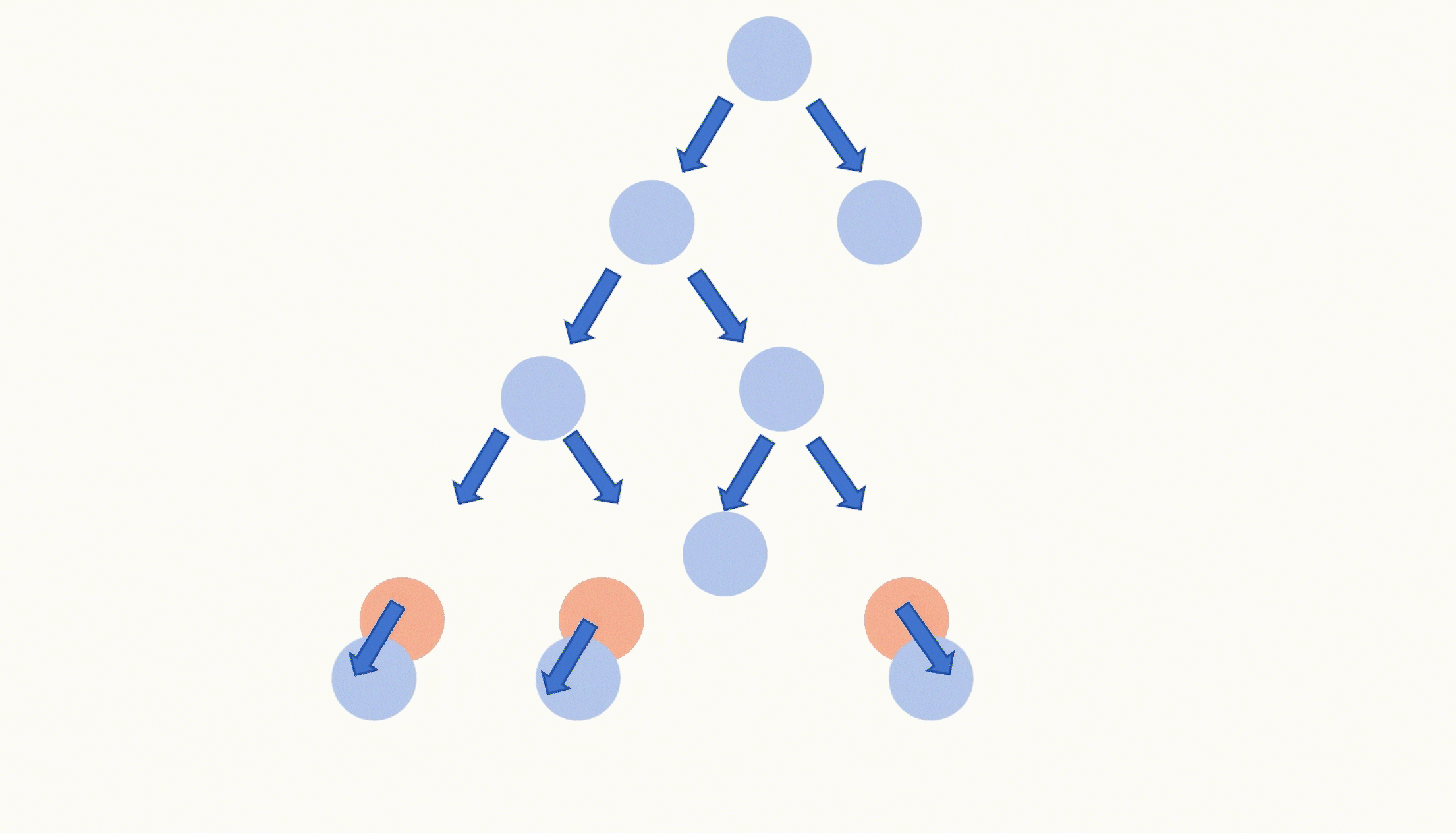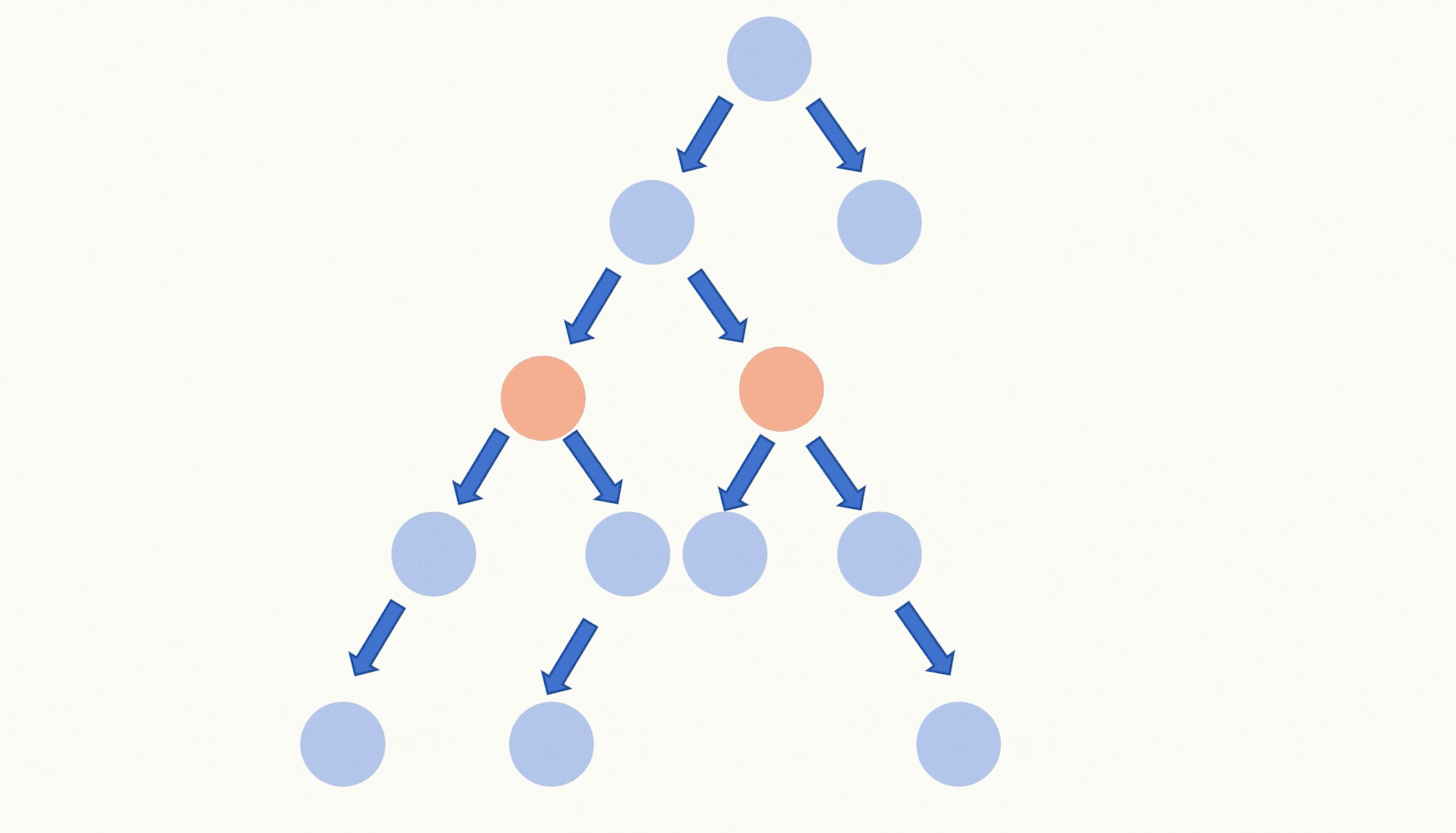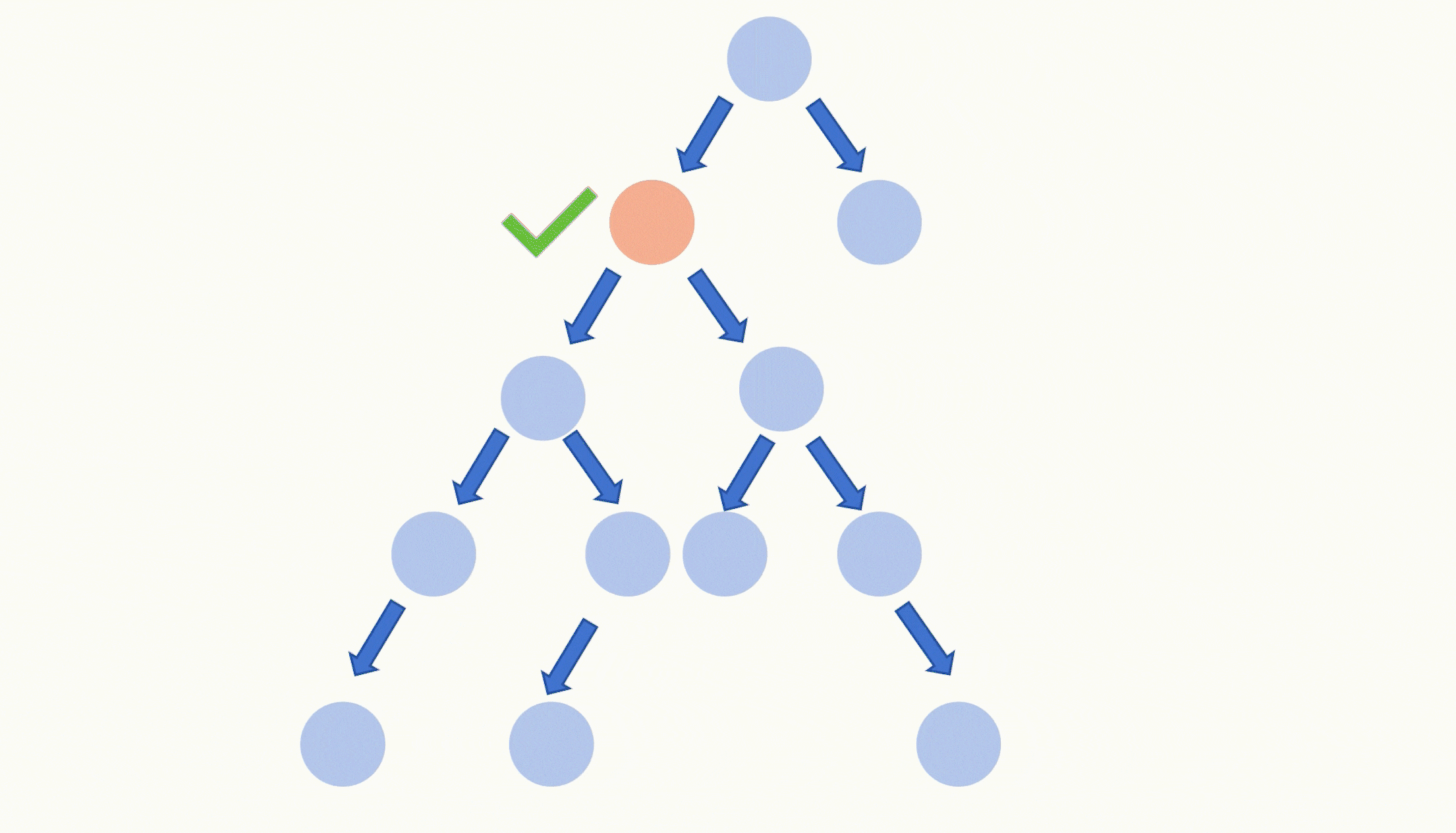
题目给我们一棵二叉树，让我们找出所有最深叶子节点的最近公共祖先。

我们一步一步剖析，我们先找出最深叶子节点，其实一棵二叉树上最深的节点一定是叶子节点，因为往下没有任何节点了。

所以我们直接找出最深的节点。跟深度有关，我们可以使用层序遍历来获取最深的节点。

获取之后我们需要找出它们的最近公共祖先。

如果最深节点只有一个，那么最近公共祖先就是他自己，如果大于一个就需要往上寻找了。

因为要往上寻找父节点，所以我们需要记录下每个节点的父子节点关系，这我们可以在层序遍历的时候一起记录。

我们先将最深节点放入一个容器里。

不断遍历这个容器，每次都将容器里的节点替换为该节点的父节点，这代表往上寻找祖先，记得要去重，因为每个节点最多有两个子节点。

直到这个容器里只剩一个节点了，那么这个节点就是这棵二叉树的所有最深叶子节点的最近公共祖先了。

由于最深节点的深度都是一致的，所以我们每次做替换为父节点操作之后，存放节点的容器里的所有节点还是在同一个深度。所以直到同一个深度上只有一个节点的时候，这个节点就是公共祖先了。

代码：

class Solution {
public:
    unordered_map<TreeNode*,TreeNode*>m;    //记录父子节点关系
    vector<vector<TreeNode*>>cache;         //记录层序遍历结果
    void find(TreeNode* root,int deep){     //DFS层序遍历
        if(root==nullptr) return;
        if(cache.size()<=deep) cache.push_back(vector<TreeNode*>(0));
        cache[deep].push_back(root);
        if(root->left){
            m[root->left]=root;     //记录父子节点
            find(root->left,deep+1);
        }
        if(root->right){
            m[root->right]=root;    //记录父子节点
            find(root->right,deep+1);
        }
    }
    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        find(root,0);
        vector<TreeNode*>res=cache.back();  //获取最后一层的节点
        while(res.size()>1){                //直到最后一层的父节点节点变成同一个才退出循环
            unordered_set<TreeNode*>s;
            for(int i=0;i<res.size();i++){
                s.insert(m[res[i]]);        //往上寻找每个节点的父节点
            }
            
            res=vector<TreeNode*>(s.begin(),s.end());
        }
        return res[0];
    }
};