1.场景
用于计算一个节点到其他节点的最短路径,特点是由其实点位中心向外层扩展(BFS思想),直至扩展到终点为止
2.认识
https://blog.csdn.net/weixin_57128596/article/details/126982769?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167118977016800180635372%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=167118977016800180635372&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2blogfirst_rank_ecpm_v1~rank_v31_ecpm-1-126982769-null-null.nonecase&utm_term=BFS&spm=1018.2226.3001.4450

思路图示:
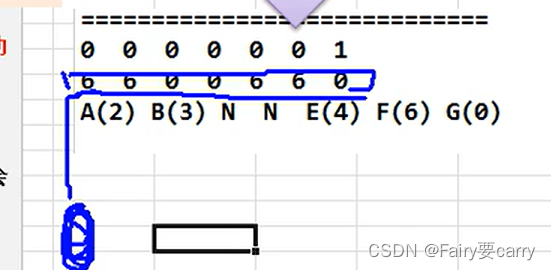
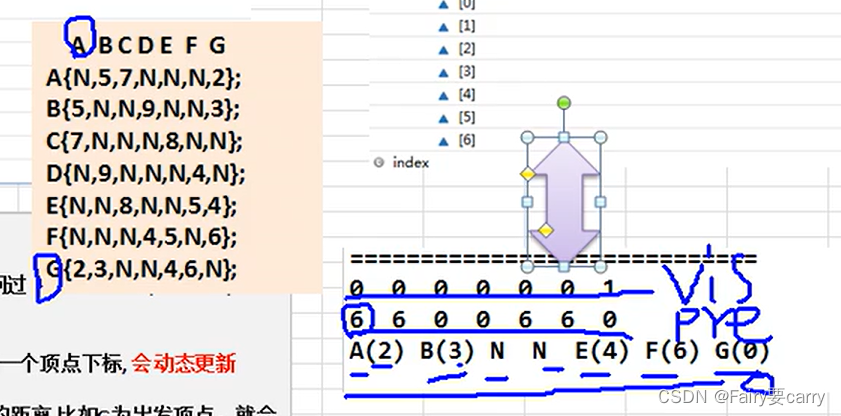
比如G为顶点将其注入,然后遍历已经访问的顶点集合Visited_vertex,通过这个已经访问的顶点集合进行扩散,遍历矩阵中没有访问的,并且动态更新节点之前的距离,最短距离放在dis[]中,体现BFS的地方:遍历过的节点也就是比如G得到周围节点一条最短的GB,那么B就被加入到队列中了,进行横向的扩展,下次遍历就会有B节点,通过B节点得到下一步的最小路径(新的出发点)
然后解释一下这个图
这个图是前去节点数组pre_visited[],每个下标对应的值=前一个的顶点下标,比如下面下标为0,对应的值为6说明前一个点的下标为6
3.应用
- 首先得设置出发顶点 v,顶点集合V{v1,v2,v3…},v到V中各个顶点的距离构成的距离集合为Dis{d1,d2,d3…},Dis记录着v顶点到其他顶点的距离,自身可以看作为0
- 从Dis中选择最小的di并且移除Dis集合,同时移除V集合中对应的顶点vi,v到vi的最短路径就出来了
- 每次都要更新Dis集合,规则为:比较v到V集合顶点的距离值,保留较小的一个(同时更新前驱节点状态,并且已经访问)
- 重复执行以上两步骤,直到最短路径顶点为目标顶点即可结束
简单来说:
- 把出发顶点作为当前节点cur,把当前节点标记为已访问,开始访问各个节点j(0 <= j <= n),更新dis(出发节点到当前节点的距离)和pre,更新规则:若dis[j] < dis[cur] + max[cur][j]则更新dis和pre
- 选出未被访问过的节点,且dis最小的节点作为当前节点
- 重复上述步骤,直到所有节点都已被访问
迪杰斯特拉(Dijkstra)算法最佳应用-最短路径
强调的是顶点到所有顶点的距离,每个怎么样才能是最短
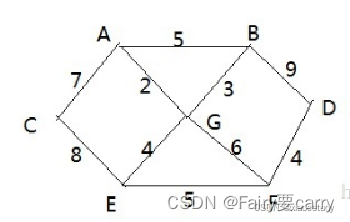
1.战争时期,胜利乡有 7 个村庄(A, B, C, D, E, F, G) ,现在有六个邮差,从 G 点出发,需要分别把邮件分别送到A, B, C , D, E, F 六个村庄
2.各个村庄的距离用边线表示(权) ,比如 A – B 距离 5 公里
3.问:如何计算出 G 村庄到 其它各个村庄的最短距离?
4.如果从其它点出发到各个点的最短距离又是多少?
使用图解的方式分析了迪杰斯特拉(Dijkstra)算法 思路
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
//邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;// 表示不可以连接
matrix[0]=new int[]{N,5,7,N,N,N,2};
matrix[1]=new int[]{5,N,N,9,N,N,3};
matrix[2]=new int[]{7,N,N,N,8,N,N};
matrix[3]=new int[]{N,9,N,N,N,4,N};
matrix[4]=new int[]{N,N,8,N,N,5,4};
matrix[5]=new int[]{N,N,N,4,5,N,6};
matrix[6]=new int[]{2,3,N,N,4,6,N};
//创建 Graph对象
Graph graph = new Graph(vertex, matrix);
//测试, 看看图的邻接矩阵是否ok
graph.showGraph();
//测试迪杰斯特拉算法
graph.dsj(2);//C
graph.showDijkstra();
}
}
class Graph {
private char[] vertex; // 顶点数组
private int[][] matrix; // 邻接矩阵
private VisitedVertex vv; //已经访问的顶点的集合
// 构造器
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
//显示结果
public void showDijkstra() {
vv.show();
}
// 显示图
public void showGraph() {
for (int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}
//迪杰斯特拉算法实现
/**
*
* @param index 表示出发顶点对应的下标
*/
public void dsj(int index) {
vv = new VisitedVertex(vertex.length, index);
update(index);//更新index顶点到周围顶点的距离和前驱顶点
for(int j = 1; j <vertex.length; j++) {
index = vv.updateArr();// 选择并返回新的访问顶点
update(index); // 更新index顶点到周围顶点的距离和前驱顶点
}
}
//更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点,
private void update(int index) {
int len = 0;
//根据遍历我们的邻接矩阵的 matrix[index]行
for(int j = 0; j < matrix[index].length; j++) {
// len 含义是 : 出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
len = vv.getDis(index) + matrix[index][j];
// 如果j顶点没有被访问过,并且 len 小于出发顶点到j顶点的距离,就需要更新
if(!vv.in(j) && len < vv.getDis(j)) {
vv.updatePre(j, index); //更新j顶点的前驱为index顶点
vv.updateDis(j, len); //更新出发顶点到j顶点的距离
}
}
}
}
// 已访问顶点集合
class VisitedVertex {
// 记录各个顶点是否访问过 1表示访问过,0未访问,会动态更新
public int[] already_arr;
// 每个下标对应的值为前一个顶点下标, 会动态更新
public int[] pre_visited;
// 记录出发顶点到其他所有顶点的距离,比如G为出发顶点,就会记录G到其它顶点的距离,会动态更新,求的最短距离就会存放到dis
public int[] dis;
//构造器
/**
*
* @param length :表示顶点的个数
* @param index: 出发顶点对应的下标, 比如G顶点,下标就是6
*/
public VisitedVertex(int length, int index) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
//初始化 dis数组
Arrays.fill(dis, 65535);
this.already_arr[index] = 1; //设置出发顶点被访问过
this.dis[index] = 0;//设置出发顶点的访问距离为0
}
/**
* 功能: 判断index顶点是否被访问过
* @param index
* @return 如果访问过,就返回true, 否则访问false
*/
public boolean in(int index) {
return already_arr[index] == 1;
}
/**
* 功能: 更新出发顶点到index顶点的距离
* @param index
* @param len
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/**
* 功能: 更新pre这个顶点的前驱顶点为index顶点
* @param pre
* @param index
*/
public void updatePre(int pre, int index) {
pre_visited[pre] = index;
}
/**
* 功能:返回出发顶点到index顶点的距离
* @param index
*/
public int getDis(int index) {
return dis[index];
}
/**
* 继续选择并返回新的访问顶点, 比如这里的G 完后,就是 A点作为新的访问顶点(注意不是出发顶点)
* @return
*/
public int updateArr() {
int min = 65535, index = 0;
for(int i = 0; i < already_arr.length; i++) {
if(already_arr[i] == 0 && dis[i] < min ) {
min = dis[i];
index = i;
}
}
//更新 index 顶点被访问过
already_arr[index] = 1;
return index;
}
//显示最后的结果
//即将三个数组的情况输出
public void show() {
System.out.println("==========================");
//输出already_arr
for(int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
//输出pre_visited
for(int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
//输出dis
for(int i : dis) {
System.out.print(i + " ");
}
System.out.println();
//为了好看最后的最短距离,我们处理
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int count = 0;
for (int i : dis) {
if (i != 65535) {
System.out.print(vertex[count] + "("+i+") ");
} else {
System.out.println("N ");
}
count++;
}
System.out.println();
}
}










![[附源码]Nodejs计算机毕业设计基于网络C++实验管理系统Express(程序+LW)](https://img-blog.csdnimg.cn/dc9dce23010844599b2a8300c59ac942.png)