目录

摘要

1 概述

2 数学模型与方法

3 讲解

3.1 测试1 

3.2 测试2 

3.3 测试3 

3.4 测试4 

4 Matlab代码实现

---

摘要

提出了一种无需通量校正的高效电晕放电模拟算法。称为位置-状态分离 (POSS) 方法的算法用于求解电晕放电建模中通常存在的以对流为主的连续性方程。所提出的求解方法结合了用于求解对流加速度、扩散和反应子问题的欧拉方案，以及用于求解线性对流子问题的拉格朗日方案。在不同维度和坐标系中进行了几个经典的数值实验，以证明 POSS 在低计算成本、鲁棒性和高分辨率方面的优异性能。结果表明，该方法在处理带电粒子对流时的时间复杂度随着未知数的增加而线性增加。对于局部电场不会随时间发生强烈变化的电晕放电的模拟，POSS 的时间步长可能比 Courant-Friedrichs-Lewy 时间步长大得多。这些特殊功能使 POSS 在模拟长电极间间隙和长时间模拟的电晕放电方面具有巨大潜力。

1 概述

当电极附近的电场变得大于电离气体所需的阈值电场时，就会发生电晕放电。当电极的特征尺寸远小于电极间距离时，就会出现这种情况，从而产生自持的局部放电 [1]。电晕放电通常有两种不同的模式：在不同配置和施加电压下的均匀辉光电晕放电和灯丝流光放电 [2]。文献中的大多数电晕放电模拟模型都遵循流体动力学近似，其中气体中带电粒子的一组连续性方程与泊松方程一起同时求解。

连续方程评估在对流整体运动、扩散运动和反应项的影响下，气体中带电粒子（电子和离子）的密度 ρ 的变化。在一般形式中，连续性方程表示为：

          

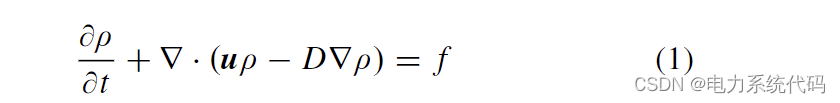
这里 u 是所考虑粒子的速度矢量，D 是扩散系数。术语 f 定义了由于不同过程而产生的源和汇，例如碰撞电离、附着、光电离、复合等。由于两个主要原因，电晕模拟中的连续性方程难以求解。首先，数值时间步长受到电子连续性方程解的限制，因为它们的移动速度比离子快两个数量级以上。其次，当过渡到流光放电时，在模拟过程中会出现 ρ 或 u 的不连续性或陡峭梯度。在这些条件下，数值方法可能会遇到一些缺点，例如人工振荡或过度的数值扩散 [3]。

一般来说，求解连续性方程的数值方法可以根据参考系分为三组：欧拉、拉格朗日和混合欧拉-拉格朗日（也称为半拉格朗日）。现在让我们简要描述一下用于模拟电晕放电的对流主导的连续性方程求解的最常用方法的主要特征。对于大多数欧拉方法，“通量限制”概念通常用于避免在使用高阶空间离散化方案时在不连续性和激波前沿发生虚假振荡。引入这一概念的第一个方法是通量校正传输 (FCT) 方法 [4]-[6]。 FCT 最初是由 Boris 和 Book [4]-[6] 提出的，用于一维均匀网格，后来 Zalesak [7] 和 Morrow 和 Cram [8] 分别提出了它对高维和非均匀网格的扩展.不久之后，引入了有限元 FCT 方法 (FEM-FCT) 来处理不规则结构 [9]、[10]。 FEM-FCT 基于 Zalesak 处理元素贡献的 FCT 程序，后来通过引入各个节点之间的双边质量交换对其进行了修改 [11]。然而，Zalesak 的通量限制策略非常耗时。遵循概念。

总之，一种适用于电晕放电建模的改进数值方法应该能够在发生丝状流光电晕放电时，在存在激波前沿、不连续性或陡峭梯度的情况下提供准确、稳定和非负的解；简单快速，这意味着该算法易于实现且计算成本低，以适应电晕放电的多尺度物理变化；易于在非结构化网格上实现，因为存在电晕放电的几何形状通常是不规则的，例如点对板或导体对板配置；可扩展到高维和其他坐标系，例如在模拟电晕放电时经常使用的柱坐标系；并且对于并行计算处理高维模型中的巨大未知数是可行的。

2 数学模型与方法

电晕放电建模的目标是准确估计任何时间任何粒子的分布。为了实现这一目标，必须计算不稳定粒子流的三个基本要素——时间、位置和状态。在求解连续性方程时，由于密度 ρ 的时间和空间离散化都混合在一个方程中，因此会出现困难。为了规避这一点，POSS 使用将密度 ρ 的位置和状态的瞬态解拆分为两个不同的数值问题的概念，并为每个问题使用最合适的求解方法。

让我们首先考虑具有恒定扩散系数 D 的一维连续性方程。然后，（1）重写为：

           

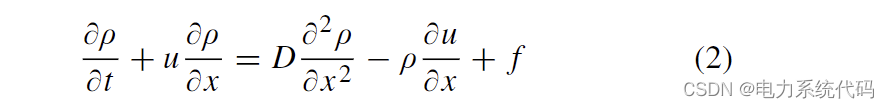
这里x ∈ [ a, b], a < b 是在空间上用n个节点的欧拉网格（以下称为参考网格）离散化的计算域。通过执行算子拆分 [27]，(2) 被分成两个不同的表达式，使得它的解近似为两个独立子问题的顺序解。

2.1 由下式给出的状态子问题

             

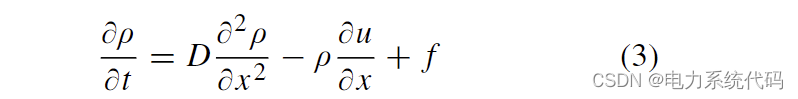
它处理由于扩散、对流加速和反应项引起的变量 ρ 的变化。该方程的解在每个时间步为第二个子问题提供了初始条件 ρ∗

2.2 给出的位置子问题

             

它仅通过考虑线性对流来确定变量 ρ 的传输。由于算子拆分与所涉及的维数无关，因此这种方法可以很容易地扩展到 2-D/3-D。重写 (3) 和 (4) ：

                  

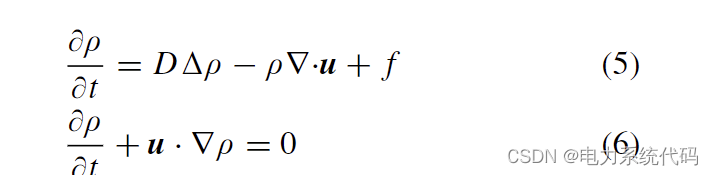
 其中密度 ρ 定义在属于有界域 ∈ Rd (d = 1, 2, 3) 的空间变量 x 和速度向量中。

3 讲解

部分代码：

%% MAIN
% 这段代码说明了如何POSS（位置-状态分离法）在模拟电晕放电。
% 高效的半拉格朗日算法用于模拟电晕放电：位置-状态分离法。
% 电晕放电模拟的高效半拉格朗日算法：位置-状态分离法。

%%
% 该代码有4个测试案例，如论文中所述。
% TestCase_1: 正方形测试
% 测试案例2：一般平流-扩散问题测试
% 测试案例3：戴维斯测试
% 测试案例4：辉光电晕测试，注意这个测试案例是非常消耗时间。

CaseToBeRun = 2;  %自行切换四种情形
if CaseToBeRun == 1
    run('./TestCase_1/SquareTest.m');
elseif CaseToBeRun ==  2
    run('./TestCase_2/GeneralAdvectionDiffusionTest.m');
elseif CaseToBeRun ==  3
    run('./TestCase_3/DaviesTest.m');
elseif CaseToBeRun ==  4
    run('./TestCase_4/CoronaTest.m');
else
    error('No such test case!');
end

 

3.1 测试1 

%% 正方形测试

%%
clc
clear
close all
tic
x1 = 0;   % 计算区域的左端
x2 = 1;   % 计算区域的右端
ng = 200; % 网格的未知数
xg = linspace(x1,x2,ng)'; % 位置
ug = zeros(ng,1); % 密度
ug(find(xg>=0.1 & xg<=0.2)) = 1; % 初始条件
vg = zeros(ng,1); % 速度
vg = vg+1;
xp = xg;
up = ug;
%
T = 1; % 仿真时间
saveTime = [0.3*T;0.6*T]; % 何时绘制
dt = [2e-2 2e-3 2e-4];    % 时间步长
lineTpye = {'r--','m-.','b:'};
%% 绘制分析解决方案
figure; box on; hold on
plot(xg,ug,'k-','LineWidth',1.2);
for i = 1:length(saveTime)
    ug1 = ug;
    ug1(find(xg >= 0.1 + saveTime(i)*vg & xg <= 0.2 + saveTime(i)*vg)) = 1;
    plot(xg,ug1,'k-','LineWidth',1.2);
end
text(0.11,1.2,'t = 0')
text(0.41,1.2,'t = 0.3')
text(0.71,1.2,'t = 0.6')
xlabel('位置')
ylabel('密度')
%% 运行
for i = 1:length(dt)
    t = 0; xg2 = xg; ug2 = ug;
    saveTime2 = [saveTime;saveTime(end)*2];
    for t=0:dt(i):T
        % 重置网格
        xp = xg2;
        up = ug2;
        % 可视化
        if abs(t - saveTime2(1))<dt(i)/2;
            saveTime2(1)=[];
            plot(xg2,ug2,lineTpye{i},'LineWidth',1.2);
            hold on
            axis([x1 x2 -0.3 1.3])
            drawnow
        end
        % 求解位置方程得到辅助网格( xp )。
        xp = xp+vg*dt(i);
        % 从辅助网格到参考网格的插值( xg2 )
        ug2 = interp1(xp,up,xg2,'linear','extrap'); %线性插值
        %         ug2 = interp1(xp,up,xg2,'spline','extrap'); % 三次插值
        %         ug2 = interp1(xp,up,xg2,'PCHIP','extrap'); %分段三次插值
        % 边界条件
        if i>1
            ug2(1) = 0;
            ug2(end) = 0;
        end
    end
end
toc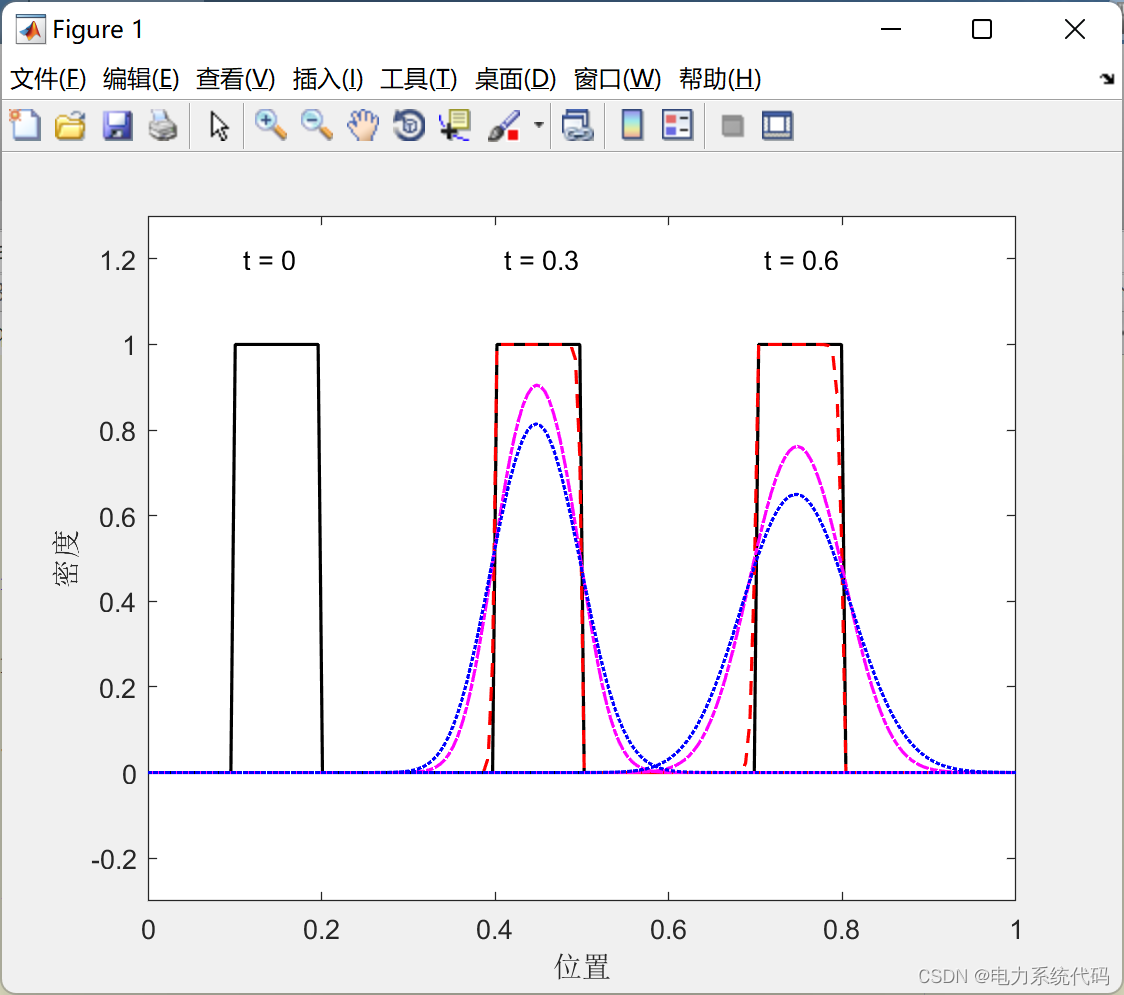

3.2 测试2 

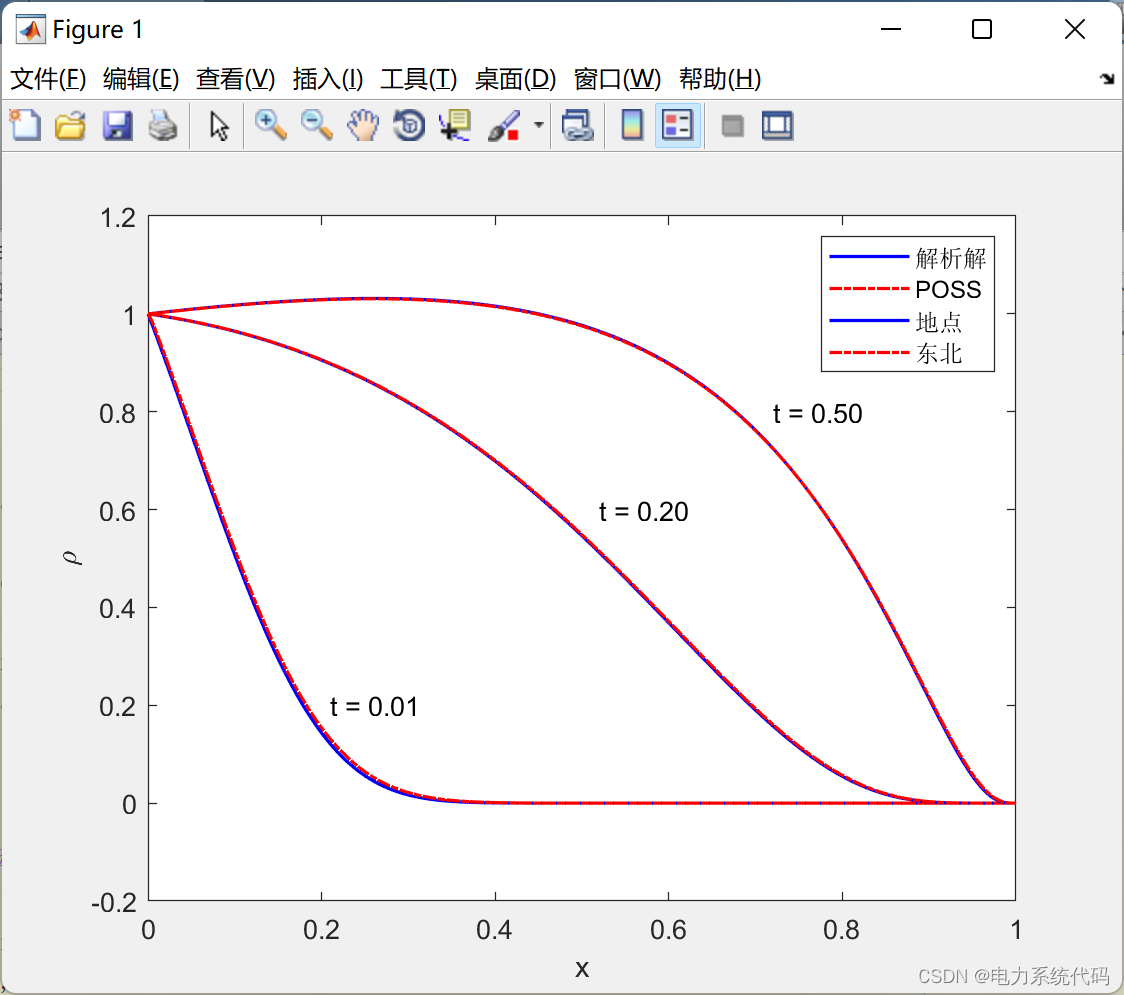
3.3 测试3 

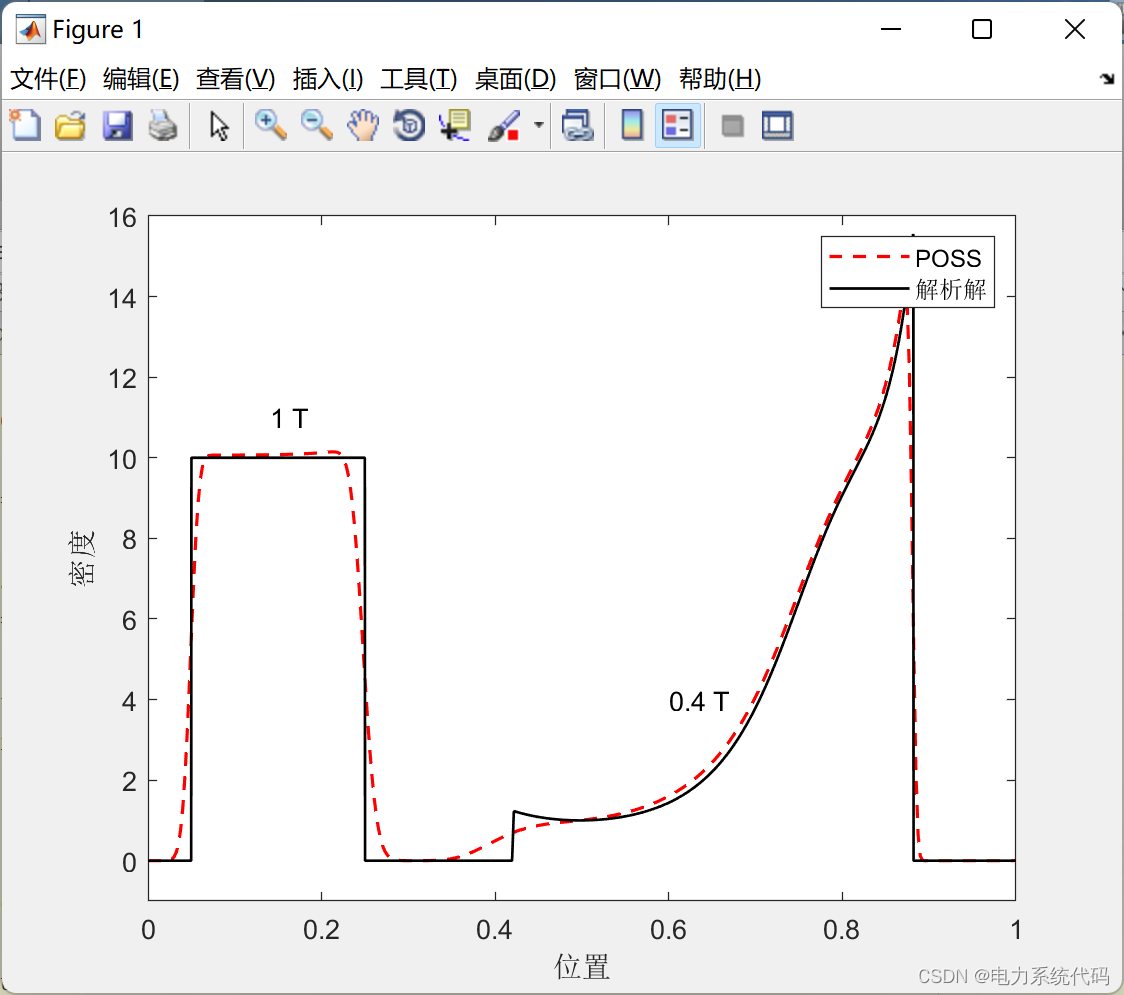
3.4 测试4 

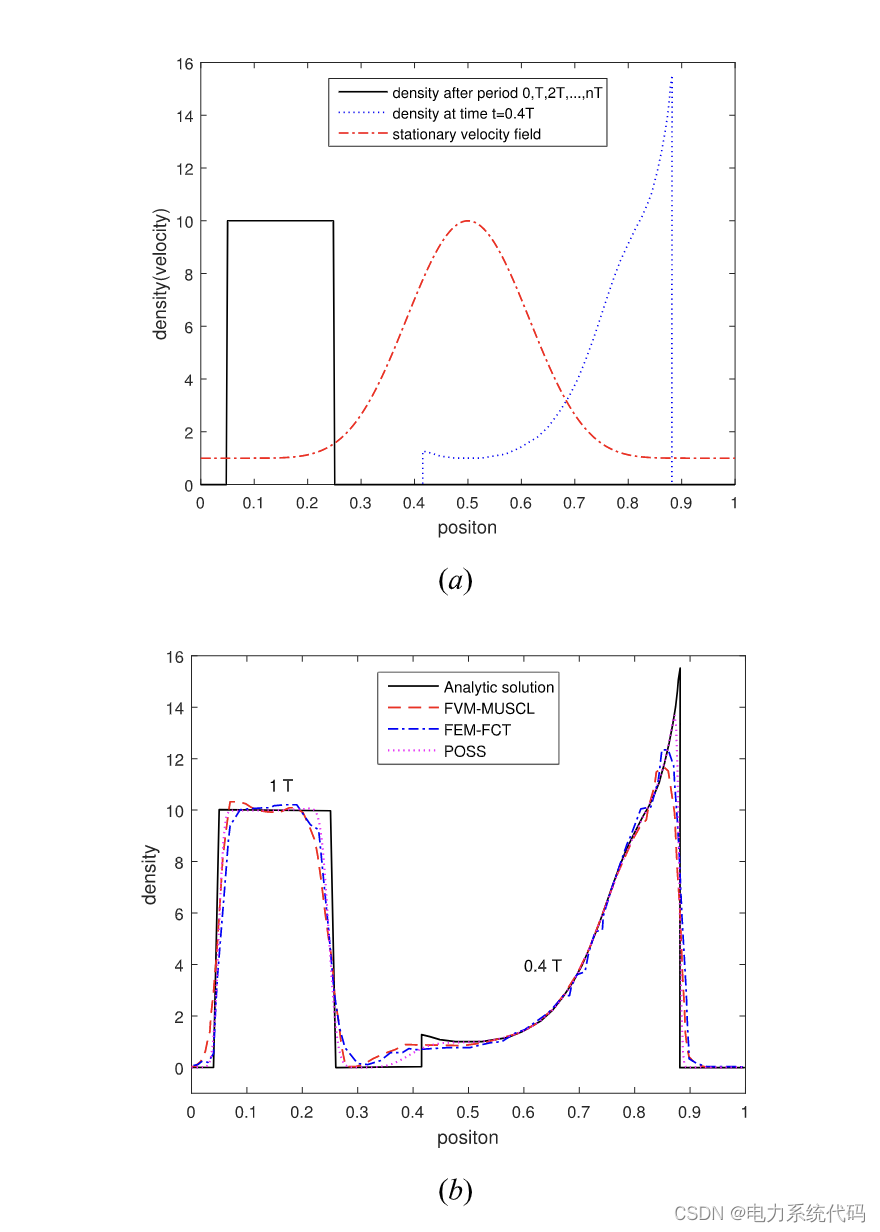
4 Matlab代码实现

一种用于模拟电晕放电的高效半拉格朗日算法