使用流

归约

到目前为止，见到过的终端操作都是返回一个boolean(allMatch之类的)、void(forEach)或optional对象(findAny等)。也见过了使用collect来将流中的所有元素组合成一个List。

如何把一个流中的元素组合起来，使用reduce操作来表达更复杂的查询，比如“计算菜单中的总卡路里”或“菜单中卡路里最高的菜是哪一个”。此类查询需要将流中所有元素反复结合起来，得到一个值，比如一个Integer。这样的查询可以被归类为归约操作(将流归约成一个值)。用函数式编程语言的术语来说，这称为折叠(fold),因为可以将这个操作看成把一张长长的纸(流)反复折叠成一个小方块，而这就是折叠操作的结果。

元素求和

先来看看如何使用for-each循环来对数字列表中的元素求和：

int sum = 0;
for(int x : numbers) {
	sum += x;
}

numbers中的每个元素都用加法运算符反复迭代来得到结果。通过反复使用加法，把一个数字列表归约成了一个数字。这段代码中有两个参数：

总和变量的初始值，在这里是0;
将列表中所有元素结合在一起的操作，在这里是+。

reduce操作还能把所有的数字相乘，而不必去复制粘贴这段代码，它对这种重复应用的模式做了抽象。可以像下面这样对流中所有的元素求和：

int sum = numbers.stream().reduce(0, (a, b) -> a + b);

reduce接受两个参数：

一个初始值，这里是0;
一个BinaryOperator<T>来将两个元素结合起来产生一个新值，这里用的是lambda(a, b) -> a + b。

也可以把所有的元素相乘，只需要将另一个Lambda : (a, b) -> a * b传递给reduce操作就可以了：

int product = numbers.stream().reduce(1, (a, b) -> a * b);

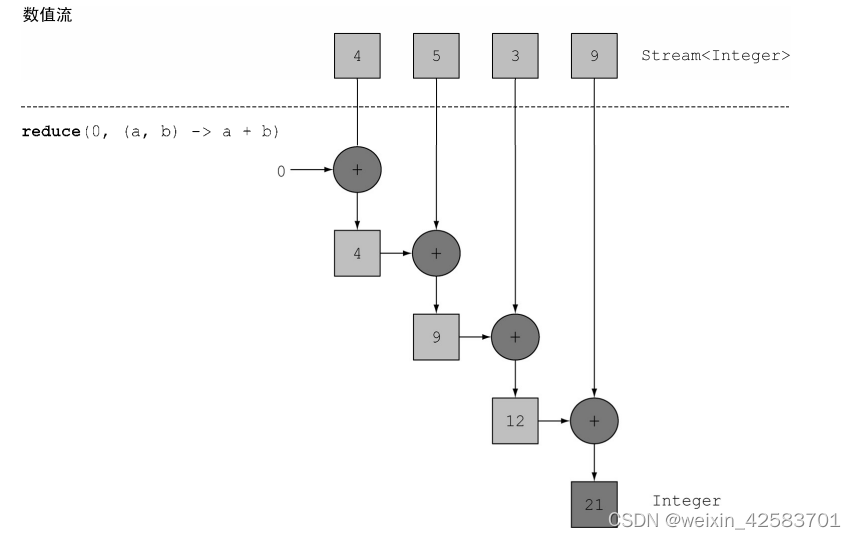
下图展示了reduce操作是如何作用于一个流的：Lambda反复结合每个元素，直到流被归约成一个值。

首先，0作为Lambda(a)的第一个参数，从流中获得4作为第二个参数(b)。0 + 4得到4,它成了新的累积值。然后再用累积值和流中下一个元素5调用Lambda,产生新的累积值9。接下来，再用累积值和下一个元素3调用Lambda,得到12。最后，用12和流中最后一个元素9调用Lambda,得到最终结果21。
在这里插入图片描述
可以使用方法引用让这段代码更简洁。在Java 8中，Integer类现在有了一个静态的sum方法来对两个数求和，这恰好是我们想要的，用不着反复用Lambda写同一段代码了：

int sum = numbers.stream().reduce(0, Integer::sum);

无初始值

reduce还有一个重载的变体，它不接受初始值，但是会返回一个optional对象：

optional<Integer> sum = numbers.stream().reduce((a, b) -> (a + b));

流中没有任何元素的情况。reduce操作无法返回其和，因为它没有初始值。这就是为什么结果被包裹在一个optional对象里，以表明和可能不存在。

最大值和最小值

利用reduce来计算流中最大或最小的元素。reduce接受两个参数：

一个初始值
一个Lambda来把两个流元素结合起来并产生一个新值

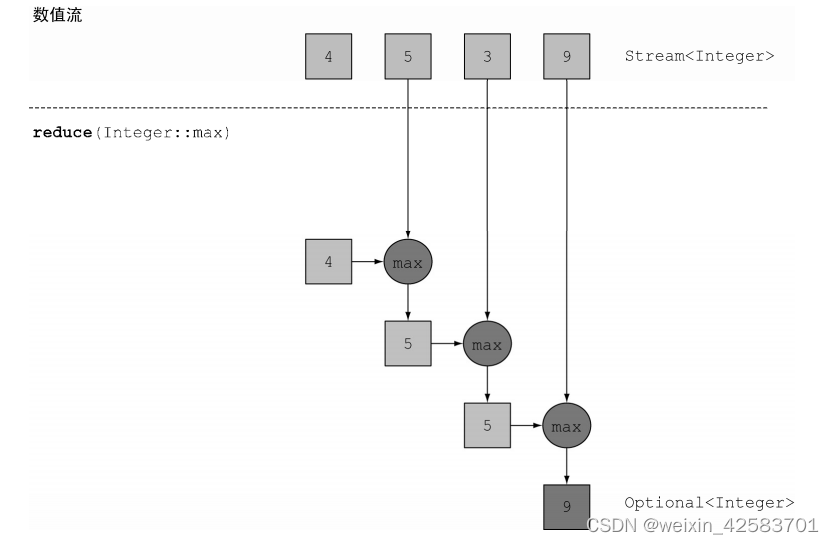
Lambda是一步步用加法运算符应用到流中每个元素上的，如下图所示。因此，需要一个给定两个元素能够返回最大值的Lambda。reduce操作会考虑新值和流中下一个元素，并产生一个新的最大值，直到整个流消耗完。可以像下面这样使用reduce来计算流中的最大值。

Optional<Integer> max = numbers.stream().reduce(Integer::max);

在这里插入图片描述
要计算最小值，需要把Integer.min传给reduce来替换Integer.max:

Optional<Integer> min = numbers.stream().reduce(Integer::min);

也可以写成Lambda(x, y) -> x < y ? x : y而不是Integer::min。

测验:归约
用map和reduce方法数一数流中有多少个菜

答案：要解决这个问题，可以把流中每个元素都映射成数字1,然后用reduce求和。这相当于按顺序数流中的元素个数。

int count = menu.stream()
.map(d -> 1)
.reduce(0,(a,b)-> a+b);
map和reduce的连接通常称为map-reduce模式，因Google用它来进行网络搜索而出名，因为它很容易并行化。内置count方法也可用来计算流中元素的个数：
long count = menu.stream().count();

归约方法的优势与并行化
相比于前面写的逐步迭代求和，使用reduce的好处在于，这里的迭代被内部迭代抽象掉了，这让内部实现得以选择并行执行reduce操作。而迭代式求和例子要更新共享变量sum,这不是那么容易并行化的。

如果加入了同步，很可能会发现线程竞争抵消了并行本应带来的性能提升!这种计算的并行化需要另一种办法：将输入分块，分块求和，最后再合并起来。但这样的话代码看起来就完全不一样了。

但现在重要的是要认识到，可变的累加器模式对于并行化来说是死路一条。需要一种新的模式，这正是reduce所提供的。

传递给reduce的Lambda不能更改状态(如实例变量),而且操作必须满足结合律才可以按任意顺序执行。

到目前为止，归约的例子包含：对流求和、流中的最大值，或是流中元素的个数。

流操作：无状态和有状态
乍一看流操作简直是灵丹妙药，而且只要在从集合生成流的时候把Stream换成parallelStream就可以实现并行。

当然，对于许多应用来说确实是这样，就像前面的那些例子。可以把一张菜单变成流，用filter选出某一类的菜肴，然后对得到的流做map来对卡路里求和，最后reduce得到菜单的总热量。
这个流计算甚至可以并行进行。但这些操作的特性并不相同。它们需要操作的内部状态还是有些问题的。

诸如map或filter等操作会从输入流中获取每一个元素，并在输出流中得到0或1个结果。这些操作一般都是无状态的：它们没有内部状态(假设用户提供的Lambda或方法引用没有内部可变状态)。

但诸如reduce、sum、max等操作需要内部状态来累积结果。在上面的情况下，内部状态很小。在例子里就是一个int或double。不管流中有多少元素要处理，内部状态都是有界的。

相反，诸如sort或distinct等操作一开始都和filter和map差不多——都是接受一个流，再生成一个流(中间操作),但有一个关键的区别。从流中排序和删除重复项时都需要知道先前的历史。
例如，排序要求所有元素都放入缓冲区后才能给输出流加入一个项目，这一操作的存储要求是无界的。要是流比较大或是无限的，就可能会有问题。这些操作叫作有状态操作。

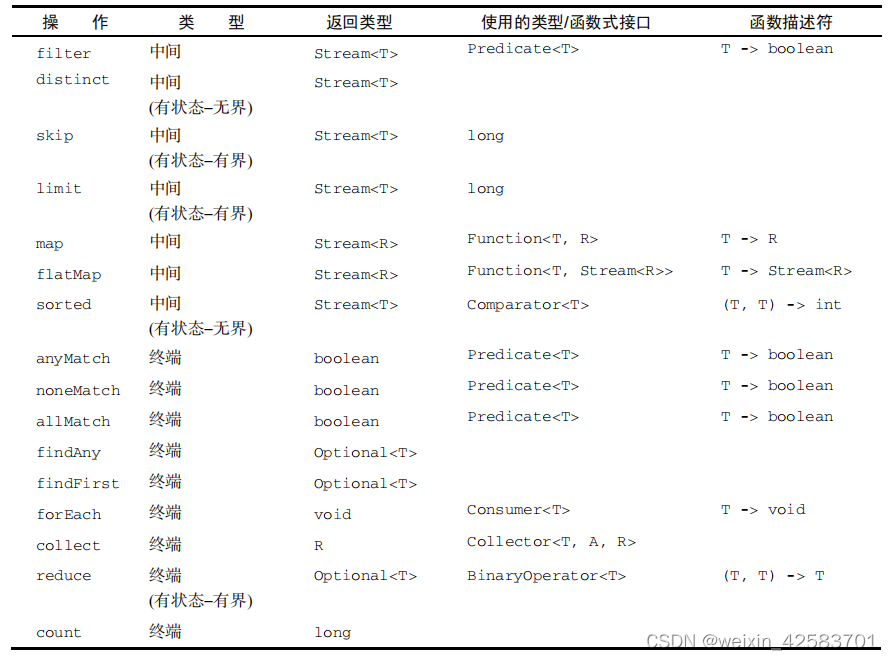
下表是对上述操作的总结：在这里插入图片描述