1143.最长公共子序列

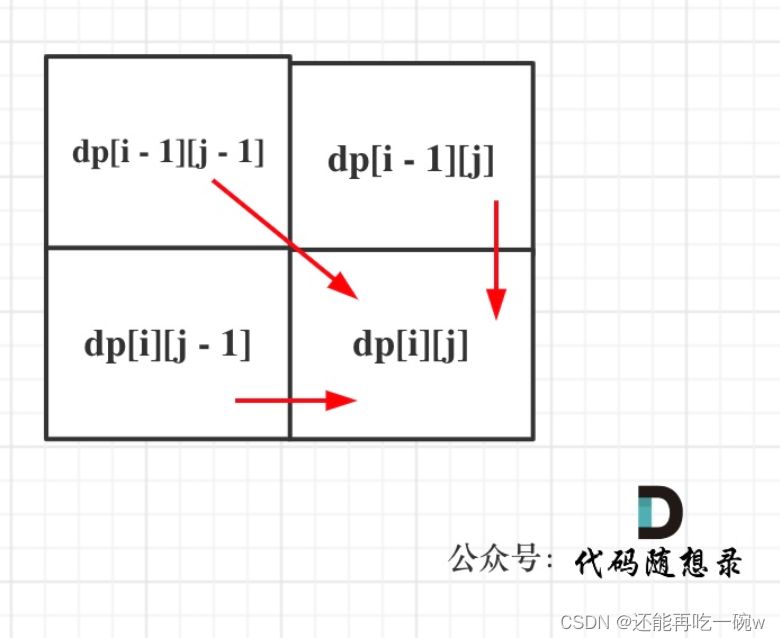
func longestCommonSubsequence(text1 string, text2 string) int {
    res := 0
    dp := make([][]int, len(text1) + 1)
    for i := 0; i <= len(text1);i++{
        dp[i] = make([]int, len(text2) + 1)
    }

    for i := 1; i <= len(text1); i++{
        for j := 1; j <= len(text2); j++{
            if text1[i - 1] == text2[j - 1]{
                dp[i][j] = dp[i - 1][j - 1] + 1
            }else{
                dp[i][j] =  max(dp[i - 1][j - 1], dp[i][j - 1])
                dp[i][j] = max(dp[i][j], dp[i - 1][j])
            }
            res = max(res, dp[i][j])
        }
    }
    return res
}
func max(a, b int)int{
    if a < b{
        return b
    }
    return a
}

1035.不相交的线

和上一题最长公共子序列的思想一模一样

53. 最大子序和 动态规划

两种方法，一种是滑动窗口，sum小于0就重新开始；
另一种是动态规划的方式，dp【i】是以i为结尾的子序列最大和，那么就是看i - 1的dp是否大于0，大于零就加上，否则就只加自己的nums【i】

func maxSubArray(nums []int) int {
   /*
    start := 0
    end := 0
    max := nums[0]
    for start < len(nums) && end < len(nums){
        sum := nums[start]
        max = int(math.Max(float64(max), float64(sum)))
        for end < len(nums) && sum >= 0{
            max = int(math.Max(float64(max), float64(sum)))
            end++
            if end < len(nums){
                sum += nums[end]
            }
            
        }
        start = end + 1
        end = start
        
    }
    return max
    */
    res := nums[0]
    dp := make([]int, len(nums))
    dp[0] = nums[0]
    for i := 1; i < len(dp); i++{
        if dp[i - 1] > 0{
            dp[i] = nums[i] + dp[i - 1]
        }else{
            dp[i] = nums[i]
        }
        res = int(math.Max(float64(res), float64(dp[i])))
    }
    return res
}