文章目录
- 一、不定积分的概念与基本性质
- 1.1 原函数与不定积分的基本概念
- 1.2 不定积分的基本性质
- 二、不定积分基本公式与积分法
- 2.1 不定积分基本公式
- 2.2 不定积分的积分法
- 2.2.1 换元积分法
- 2.2.2 分部积分法
- 三、两类重要函数的不定积分——有理函数与三角有理函数
- 3.1 有理函数的积分
- 3.2 三角有理函数的不定积分
一、不定积分的概念与基本性质
1.1 原函数与不定积分的基本概念
划重点
- 连续函数一定存在原函数,反之不对。
- 有第一类间断点的函数一定不存在原函数,但有第二肋间断点的函数可能有原函数。
- 若f(x)有原函数,则它一定有无数个原函数,且任意两个原函数之间相差常数。
- 偶函数的原函数不一定是奇函数,奇函数的原函数一定是偶函数。
1.2 不定积分的基本性质
- ∫ [ f ( x ) ± g ( x ) ] d x \int[f(x) ± g(x)]dx ∫[f(x)±g(x)]dx = ∫ f ( x ) d x ± ∫ g ( x ) d x \int f(x)dx ± \int g(x)dx ∫f(x)dx±∫g(x)dx
- ∫ k f ( x ) d x \int kf(x)dx ∫kf(x)dx = k ∫ f ( x ) d x \int f(x)dx ∫f(x)dx(k ≠ 0)
二、不定积分基本公式与积分法
2.1 不定积分基本公式
| 不定积分 | 原函数 |
|---|---|
| ∫ k d x \int kdx ∫kdx | kx + C |
| ∫ x a d x \int x\ ^adx ∫x adx | 1 a + 1 x a + 1 \frac{1}{a + 1}x\ ^{a + 1} a+11x a+1 + C |
| ∫ 1 x d x \int \frac{1}{x}dx ∫x1dx | ln|x| + C(x ≠ 0) |
| ∫ a x d x \int a\ ^xdx ∫a xdx | a x l n a \frac{a\ ^x}{ln a} lnaa x + C(a > 0,a ≠ 1) |
| ∫ e x d x \int e\ ^xdx ∫e xdx | ex + C |
| ∫ s i n x d x \int sin xdx ∫sinxdx | -cos x + C |
| ∫ c o s x d x \int cos xdx ∫cosxdx | sin x + C |
| ∫ t a n t x d x \int tant xdx ∫tantxdx | -ln|cos x| + C |
| ∫ c o t x d x \int cot xdx ∫cotxdx | ln|sin x| + C |
| ∫ s e c x d x \int sec xdx ∫secxdx | ln|sec x + tan x| + C |
| ∫ c s c x d x \int csc xdx ∫cscxdx | ln|csc x - cot x| + C |
| ∫ s e c 2 x d x \int sec\ ^2xdx ∫sec 2xdx | tan x + C |
| ∫ c s c 2 x d x \int csc\ ^2xdx ∫csc 2xdx | -cot x + C |
| ∫ s e c x t a n x d x \int sec xtan xdx ∫secxtanxdx | sec x + C |
| ∫ c s c x c o t x d x \int csc xcot xdx ∫cscxcotxdx | -csc x + C |
| ∫ d x 1 − x 2 \int \frac{dx}{\sqrt[]{1 - x\ ^2}} ∫1−x 2dx | arcsin x + C |
| ∫ d x a 2 − x 2 \int \frac{dx}{\sqrt[]{a\ ^2 - x\ ^2}} ∫a 2−x 2dx | arcsin x a \frac{x}{a} ax + C(a > 0) |
| ∫ d x 1 + x 2 \int \frac{dx}{1 + x\ ^2} ∫1+x 2dx | arctan x + C |
| ∫ d x a 2 + x 2 \int \frac{dx}{a\ ^2 + x\ ^2} ∫a 2+x 2dx | 1 a a r c t a n x a \frac{1}{a}arctan\frac{x}{a} a1arctanax + C(a ≠ 0) |
| ∫ d x x 2 − a 2 \int \frac{dx}{x\ ^2 - a\ ^2} ∫x 2−a 2dx | 1 2 a l n ∣ x − a x + a ∣ \frac{1}{2a}ln|\frac{x - a}{x + a}| 2a1ln∣x+ax−a∣ + C(a ≠ 0) |
| ∫ d x x 2 + a 2 \int \frac{dx}{\sqrt[]{x\ ^2 + a\ ^2}} ∫x 2+a 2dx | ln(x + x 2 + a 2 \sqrt[]{x\ ^2 + a\ ^2} x 2+a 2) + C |
| ∫ d x x 2 − a 2 \int \frac{dx}{\sqrt[]{x\ ^2 - a\ ^2}} ∫x 2−a 2dx | ln|x + x 2 − a 2 \sqrt[]{x\ ^2 - a\ ^2} x 2−a 2\ + C |
| ∫ a 2 − x 2 d x \int \sqrt[]{a\ ^2 - x\ ^2}dx ∫a 2−x 2dx | a 2 2 a r c s i n x a + x 2 a 2 − x 2 \frac{a\ ^2}{2}arcsin\frac{x}{a} + \frac{x}{2}\sqrt[]{a\ ^2 - x\ ^2} 2a 2arcsinax+2xa 2−x 2 + C(a > 0) |
2.2 不定积分的积分法
2.2.1 换元积分法
第一类换元积分法(凑微分法)
设f(u)的原函数为F(u),且u = φ(x)为可导函数,则
∫
f
[
φ
(
x
)
]
φ
′
(
x
)
d
x
\int f[φ(x)]φ'(x)dx
∫f[φ(x)]φ′(x)dx =
∫
f
[
φ
(
x
)
]
d
[
φ
(
x
)
]
\int f[φ(x)]d[φ(x)]
∫f[φ(x)]d[φ(x)] =
∫
f
(
u
)
d
u
\int f(u)du
∫f(u)du = F(u) + C = F[φ(x)] + C。
以下凑微分法需要熟练掌握
| 原积分 | 凑微分法 |
|---|---|
| ∫ f ( a x n + b ) x n − 1 d x \int f(ax\ ^n + b)x\ ^{n - 1}dx ∫f(ax n+b)x n−1dx | 1 n a ∫ f ( a x n + b ) d ( a x n + b ) \frac{1}{na}\int f(ax\ ^n + b)d(ax\ ^n + b) na1∫f(ax n+b)d(ax n+b) |
| ∫ f ( x ) 2 x d x \int \frac{f(\sqrt[]{x})}{2\sqrt[]{x}}dx ∫2xf(x)dx | ∫ f ( x ) d x \int f(\sqrt[]{x})d\sqrt[]{x} ∫f(x)dx |
| ∫ 1 x 2 f ( 1 x ) d x \int \frac{1}{x\ ^2}f(\frac{1}{x})dx ∫x 21f(x1)dx | - ∫ f ( 1 x ) d ( 1 x ) \int f(\frac{1}{x})d(\frac{1}{x}) ∫f(x1)d(x1) |
| ∫ e x f ( e x ) d x \int e\ ^xf(e\ ^x)dx ∫e xf(e x)dx | ∫ f ( e x ) d ( e x ) \int f(e\ ^x)d(e\ ^x) ∫f(e x)d(e x) |
| ∫ f ( l n x ) x d x \int \frac{f(ln x)}{x}dx ∫xf(lnx)dx | ∫ f ( l n x ) d ( l n x ) \int f(ln x)d(ln x) ∫f(lnx)d(lnx) |
| ∫ ( 1 − 1 x 2 ) f ( x + 1 x ) d x \int (1 - \frac{1}{x\ ^2})f(x + \frac{1}{x})dx ∫(1−x 21)f(x+x1)dx | ∫ f ( x + 1 x ) d ( x + 1 x ) \int f(x + \frac{1}{x})d(x + \frac{1}{x}) ∫f(x+x1)d(x+x1) |
| ∫ ( 1 + 1 x 2 ) f ( x − 1 x ) d x \int (1 + \frac{1}{x\ ^2})f(x - \frac{1}{x})dx ∫(1+x 21)f(x−x1)dx | ∫ f ( x − 1 x ) d ( x − 1 x ) \int f(x - \frac{1}{x})d(x - \frac{1}{x}) ∫f(x−x1)d(x−x1) |
| ∫ ( 1 + l n x ) f ( x l n x ) d x \int (1 + ln x)f(xln x)dx ∫(1+lnx)f(xlnx)dx | ∫ f ( x l n x ) d ( x l n x ) \int f(xln x)d(xln x) ∫f(xlnx)d(xlnx) |
| ∫ f ( s i n x ) c o s x d x \int f(sin x)cos xdx ∫f(sinx)cosxdx | ∫ f ( s i n x ) d ( s i n x ) \int f(sin x)d(sin x) ∫f(sinx)d(sinx) |
| ∫ f ( c o s x ) s i n x d x \int f(cos x)sin xdx ∫f(cosx)sinxdx | - ∫ f ( c o s x ) d ( c o s x ) \int f(cos x)d(cos x) ∫f(cosx)d(cosx) |
| ∫ f ( t a n x ) s e c 2 x d x \int f(tan x)sec\ ^2xdx ∫f(tanx)sec 2xdx | ∫ f ( t a n x ) d ( t a n x ) \int f(tan x)d(tan x) ∫f(tanx)d(tanx) |
| ∫ f ( c o t x ) c s c 2 x d x \int f(cot x)csc\ ^2xdx ∫f(cotx)csc 2xdx | - ∫ f ( c o t x ) d ( c o t x ) \int f(cot x)d(cot x) ∫f(cotx)d(cotx) |
| ∫ f ( s e c x ) s e c x t a n x d x \int f(sec x)sec xtan xdx ∫f(secx)secxtanxdx | ∫ f ( s e c x ) d ( s e c x ) \int f(sec x)d(sec x) ∫f(secx)d(secx) |
| ∫ f ( c s c x ) c s c x c o t x d x \int f(csc x)csc xcot xdx ∫f(cscx)cscxcotxdx | - ∫ f ( c s c x ) d ( c s c x ) \int f(csc x)d(csc x) ∫f(cscx)d(cscx) |
| ∫ f ( a r c s i n x ) 1 − x 2 d x \int \frac{f(arcsin x)}{\sqrt[]{1 - x\ ^2}}dx ∫1−x 2f(arcsinx)dx | ∫ f ( a r c s i n x ) d ( a r c s i n x ) \int f(arcsin x)d(arcsin x) ∫f(arcsinx)d(arcsinx) |
| ∫ f ( a r c t a n x ) 1 + x 2 d x \int \frac{f(arctan x)}{1 + x\ ^2}dx ∫1+x 2f(arctanx)dx | ∫ f ( a r c t a n x ) d ( a r c t a n x ) \int f(arctan x)d(arctan x) ∫f(arctanx)d(arctanx) |
第二类换元积分法
设φ(t)单调可导且φ’(t) ≠ 0,f(x)有原函数,则
∫
f
(
x
)
d
x
\int f(x)dx
∫f(x)dx =
∫
f
[
φ
(
t
)
]
φ
′
(
t
)
d
t
\int f[φ(t)]φ'(t)dt
∫f[φ(t)]φ′(t)dt =
∫
g
(
t
)
d
t
\int g(t)dt
∫g(t)dt = G(t) + C = G[
φ
−
1
φ\ ^{-1}
φ −1(x)] + C。
当被积函数含平方和或平方差是,一般采用三角代换,具体换元方法为
| 表达式 | 替换式 |
|---|---|
| a 2 − x 2 a\ ^2 - x\ ^2 a 2−x 2 | 令x = asin t,则 a 2 − x 2 = a 2 c o s 2 t a\ ^2 - x\ ^2 = a\ ^2cos\ ^2t a 2−x 2=a 2cos 2t |
| x 2 + a 2 x\ ^2 + a\ ^2 x 2+a 2 | 令x = atan t,则 x 2 + a 2 = a 2 s e c 2 t x\ ^2 + a\ ^2 = a\ ^2sec\ ^2t x 2+a 2=a 2sec 2t |
| x 2 − a 2 x\ ^2 - a\ ^2 x 2−a 2 | 令x = asec t,则 x 2 − a 2 = a 2 t a n 2 t x\ ^2 - a\ ^2 = a\ ^2tan\ ^2t x 2−a 2=a 2tan 2t |
倒数变换x = 1 t \frac{1}{t} t1
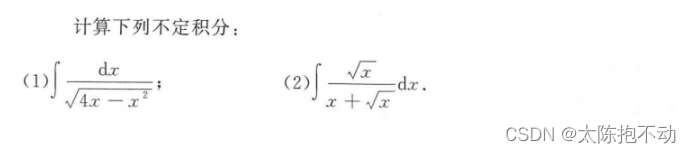
遇到
x
\sqrt[]{x}
x,想办法转换称d(
x
\sqrt[]{x}
x)。
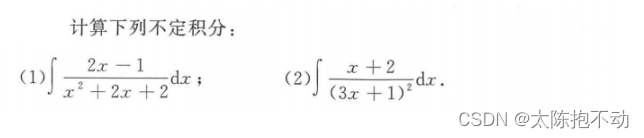

2.2.2 分部积分法
设u(x),v(x)连续可导,则分布积分公式为 ∫ u d v \int udv ∫udv = uv - ∫ v d u \int vdu ∫vdu。
以下六种情况使用分部积分公式
- ∫ x n e x d x \int x\ ^ne\ ^xdx ∫x ne xdx,即被积函数为幂函数与指数函数之积。
- ∫ x n l n x d x \int x\ ^nln xdx ∫x nlnxdx,即被积函数为幂函数与指数函数之积。
- 被积函数为幂函数与三角函数之积。
- 被积函数为幂函数与反三角函数之积。
- 被积函数为指数函数与三角函数之积。
- 被积函数为 s e c n x sec\ ^nx sec nx或 c s c n x csc\ ^nx csc nx(n为奇数)。
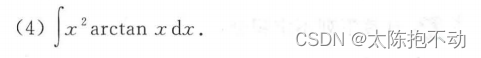
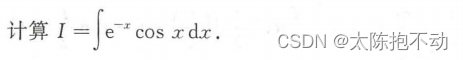
三、两类重要函数的不定积分——有理函数与三角有理函数
3.1 有理函数的积分
有理函数的概念
设R(x) = P ( x ) Q ( x ) \frac{P(x)}{Q(x)} Q(x)P(x),其中P(x),Q(x)为多项式,称R(x)为有理函数。当分子多项式P(x)的次数小于分母多项式Q(x)的次数时,称R(x)为真分式。否则,称为假分式。
有理函数的积分法
- 当R(x)为真分式时,将R(x)拆分成部分和的形式。
- 当R(x)为假分式时,将R(x)拆成多项式与真分式之和,再将真分式拆成部分和的形式。
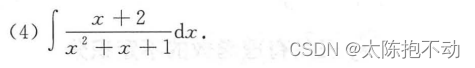
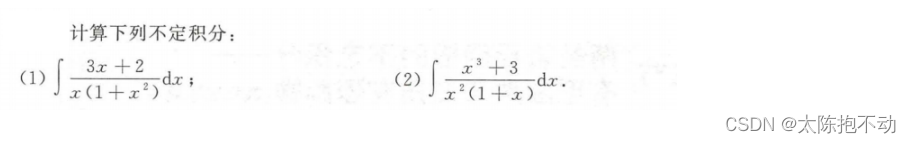
本题需要明确有理函数的拆分方法。拆分时需要关注x的幂次以及是单根还是重根。以本题为例,说明以下拆分方法。
关注x的幂次
例如, 3 x + 2 x ( 1 + x 2 ) \frac{3x + 2}{x(1 + x\ ^2)} x(1+x 2)3x+2,可以拆分成 A x \frac{A}{x} xA + B x + C 1 + x 2 \frac{Bx + C}{1 + x\ ^2} 1+x 2Bx+C。
关注是单根还是重根
例如, x 3 + 3 x 2 ( 1 + x ) \frac{x\ ^3 + 3}{x\ ^2(1 + x)} x 2(1+x)x 3+3,可以拆分成 A x \frac{A}{x} xA + B x \frac{B}{x} xB + C 1 + x \frac{C}{1 + x} 1+xC。
其实还有复数根的情况,这里没有遇到,暂不做介绍,后续遇到会进行补充。
3.2 三角有理函数的不定积分
三角有理函数的概念
设R(x,y)为二元有理函数,称R(sin x,cos x)为三角有理函数。