目录
语法
说明
示例
向量的中心移动平均值
向量的尾部移动平均值
矩阵的移动平均值
包含缺失值的向量的移动平均值
基于样本点计算移动平均值
仅返回满窗口平均值
movmean函数的功能是对数据进行移动求平均值。
语法
M = movmean(A,k)
M = movmean(A,[kb kf])
M = movmean(___,dim)
M = movmean(___,nanflag)
M = movmean(___,Name,Value)说明
M = movmean(A,k) 返回由局部 k 个数据点的均值组成的数组,其中每个均值是基于 A 的相邻元素的长度为 k 的滑动窗计算得出。当 k 为奇数时,窗以当前位置的元素为中心。当 k 为偶数时,窗以当前元素及其前一个元素为中心。当没有足够的元素填满窗时,窗将自动在端点处截断。当窗口被截断时,只根据窗口内的元素计算平均值。M 与 A 的大小相同。
-
如果 A 是向量,movmean 将沿向量 A 的长度运算。
-
如果 A 是多维数组,则 movmean 沿 A 的大小不等于 1 的第一个维度进行运算。
M = movmean(A,[kb kf]) 通过长度为 kb+kf+1 的窗口计算均值,其中包括当前位置的元素、前面的 kb 个元素和后面的 kf 个元素。
M = movmean(___,dim) 为上述任一语法指定 A 的运算维度。例如,如果 A 是矩阵,则 movmean(A,k,2) 沿 A 的列运算,计算每行的 k 元素移动均值。
M = movmean(___,nanflag) 指定包含还是省略 A 中的 NaN 值。例如,movmean(A,k,"omitnan") 在计算每个均值时会忽略 NaN 值。默认情况下,movmean 包括 NaN 值。
M = movmean(___,Name,Value) 使用一个或多个名称-值参数指定移动平均值的其他参数。例如,如果 x 是时间值向量,则 movmean(A,k,"SamplePoints",x) 相对于 x 中的时间计算移动平均值。
示例
向量的中心移动平均值
计算行向量的三点中心移动平均值。当端点处的窗口中少于三个元素时,将根据可用元素计算平均值。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,3)
M = 1×10
6.0000 6.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000 4.5000向量的尾部移动平均值
计算行向量的三点尾部移动平均值。当端点处的窗口中少于三个元素时,将根据可用元素计算平均值。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,[2 0])
M = 1×10
4.0000 6.0000 6.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000矩阵的移动平均值
计算矩阵中每行的三点中心移动平均值。窗从第一行开始,沿水平方向移动到该行的末尾,然后移到第二行,依此类推。维度参数为 2,即跨 A 的列移动窗。
A = [4 8 6; -1 -2 -3; -1 3 4]
A = 3×3
4 8 6
-1 -2 -3
-1 3 4
M = movmean(A,3,2)
M = 3×3
6.0000 6.0000 7.0000
-1.5000 -2.0000 -2.5000
1.0000 2.0000 3.5000
包含缺失值的向量的移动平均值
计算包含两个 NaN 元素的行向量的三点中心移动平均值。
A = [4 8 NaN -1 -2 -3 NaN 3 4 5];
M = movmean(A,3)
M = 1×10
6.0000 NaN NaN NaN -2.0000 NaN NaN NaN 4.0000 4.5000
重新计算平均值,但忽略 NaN 值。当 movmean 忽略 NaN 元素时,它将根据窗中的剩余元素计算平均值。
M = movmean(A,3,"omitnan")
M = 1×10
6.0000 6.0000 3.5000 -1.5000 -2.0000 -2.5000 0 3.5000 4.0000 4.5000
基于样本点计算移动平均值
根据时间向量 t,计算 A 中数据的 3 小时中心移动平均值。
A = [4 8 6 -1 -2 -3];
k = hours(3);
t = datetime(2016,1,1,0,0,0) + hours(0:5)
t = 1x6 datetime
01-Jan-2016 00:00:00 01-Jan-2016 01:00:00 01-Jan-2016 02:00:00 01-Jan-2016 03:00:00 01-Jan-2016 04:00:00 01-Jan-2016 05:00:00
M = movmean(A,k,"SamplePoints",t)
M = 1×6
6.0000 6.0000 4.3333 1.0000 -2.0000 -2.5000仅返回满窗口平均值
计算行向量的三点中心移动平均值,但在输出中舍弃使用的点数少于三个的计算。也就是说,只返回从满的三元素窗口计算的平均值,而舍弃端点计算。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,3,"Endpoints","discard")
M = 1×8
6.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000参数说明
A:输入数组,指定为向量、矩阵或多维数组。
k:窗长度,指定为数值或持续时间标量。当 k 是正整数标量时,中心平均值包括当前位置的元素以及周围的相邻元素。
例如,movmean(A,3) 计算一个由局部三点均值组成的数组。

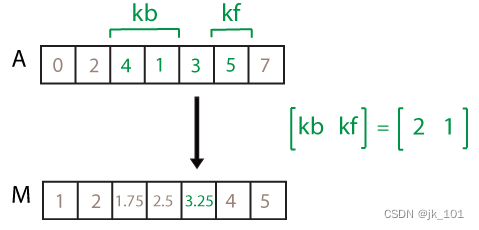
[kb kf]:定向窗长度,指定为包含两个元素的数值或持续时间行向量。当 kb 和 kf 为正整数标量时,将基于 kb+kf+1 个元素进行计算。该计算包括当前位置的元素、当前位置前面的 kb 个元素以及当前位置后面的 kf 个元素。
例如,movmean(A,[2 1]) 计算一个由局部四点均值组成的数组。
dim:沿其运算的维度,指定为正整数标量。如果不指定维度,则默认为第一个大于 1 的数组维度。
维度 dim 表示 movmean 运算所沿的维度,即指定窗的移动方向。
以一个 m×n 输入矩阵 A 为例:
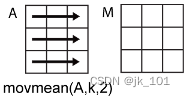
·movmean(A,k,1) 为 A 的每列计算包含 k 个元素的移动均值,并返回一个 m×n 矩阵。

·movmean(A,k,2) 为 A 的每行计算包含 k 个元素的移动均值,并返回一个 m×n 矩阵。
nanflag:缺失值条件,指定为下列值之一:
-
"includemissing" 或 "includenan" - 在计算每个均值时包括 A 中的 NaN 值。如果窗中的任一元素是 NaN,则 M 中的对应元素是 NaN。"includemissing" 和 "includenan" 具有相同的行为。
-
"omitmissing" 或 "omitnan" - 忽略 A 中的 NaN 值,并基于较少的点计算每个均值。如果窗中的所有元素都是 NaN,则 M 中的对应元素是 NaN。"omitmissing" 和 "omitnan" 具有相同的行为。