文章目录
- 题目
- 方法一:bfs广度优先 + 有向图的拓扑排序(入度)
- 方法二:dfs 深度优先搜索
题目
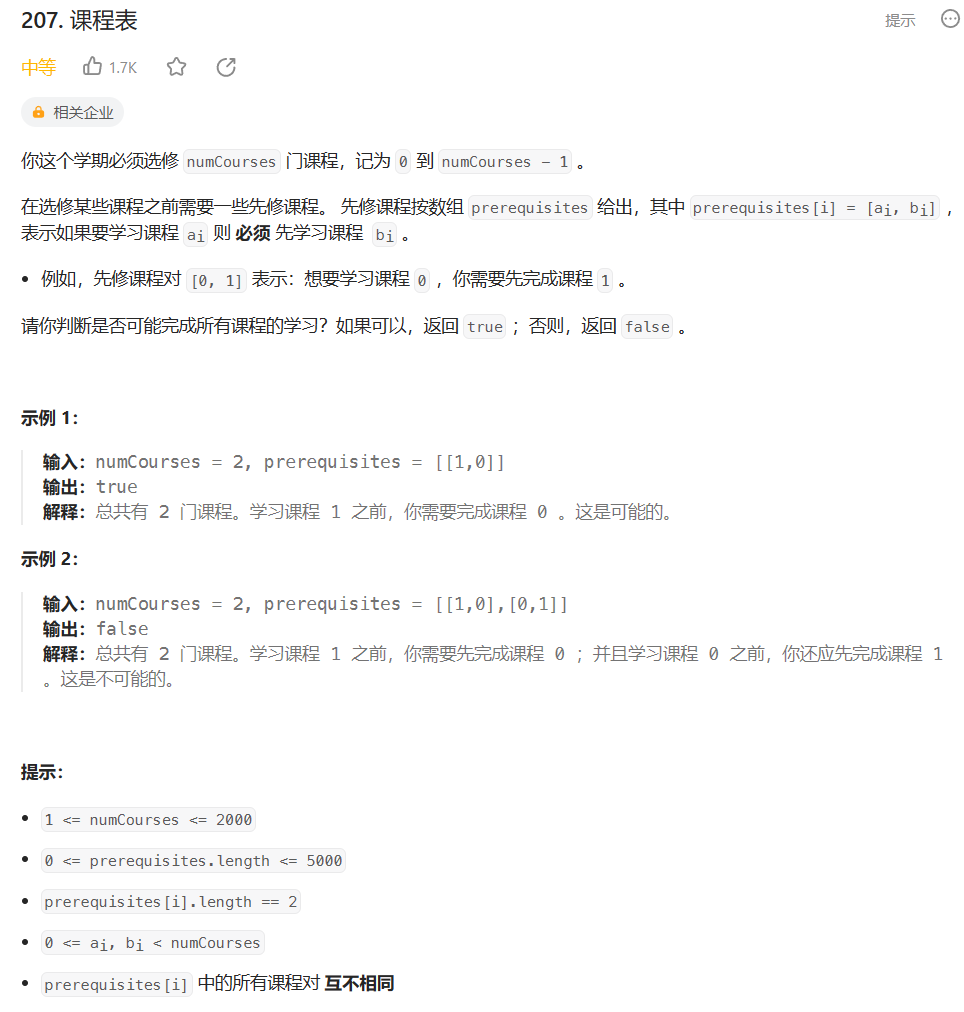

此题就可以转换为,求一个有向图是否存在环;
存在环,拓扑排序得出的结果是不完整的,
如果不存在环,则拓扑排序得出的结果就是完整的节点值(拓扑排序不唯一)
怎么判断有环和无环,就看从任意一个点出发,按照箭头方向走,会不会走到以及走过的地方,如果是就是有环
方法一:bfs广度优先 + 有向图的拓扑排序(入度)
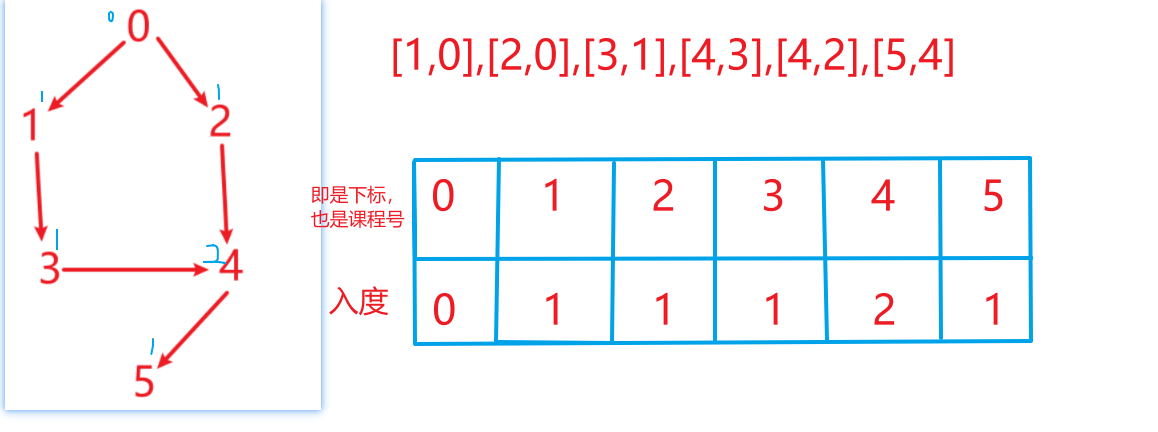
思路:将题目中的 prerequisites = [[1,0],[2,0],[3,1],[4,3],[4,2],[5,4]]数组,
按照规则prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
画出有向图:
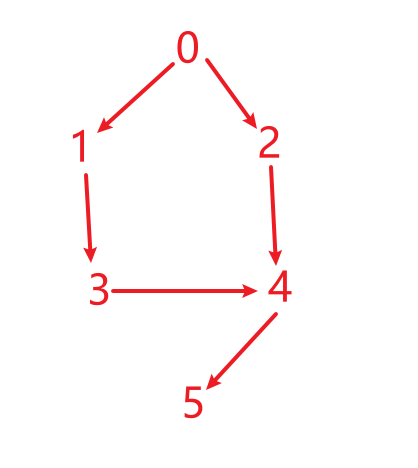
解题步骤:
-
先将题目的数组按照题目意思,转为有向图
-
构造入度数组(里面包括每个课程的入度) 课程编号 = 数组下标 数组值为入度(为什么,因为题目限制了课程号必须在课程总数内)
-
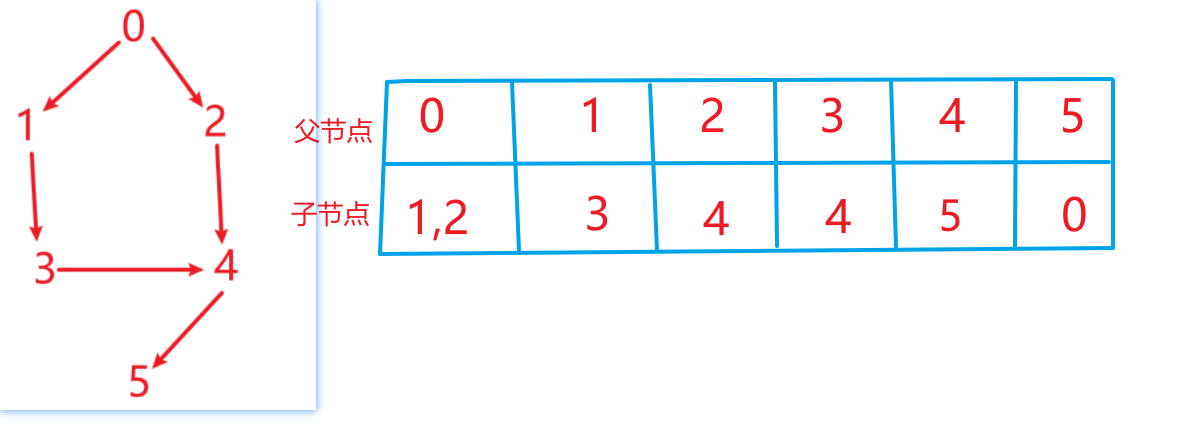
构造课程号集合,集合中每个元素同样为子集合,存储着课程号指向的课程号(记录出度指向,也就是指向元素的入度)
-
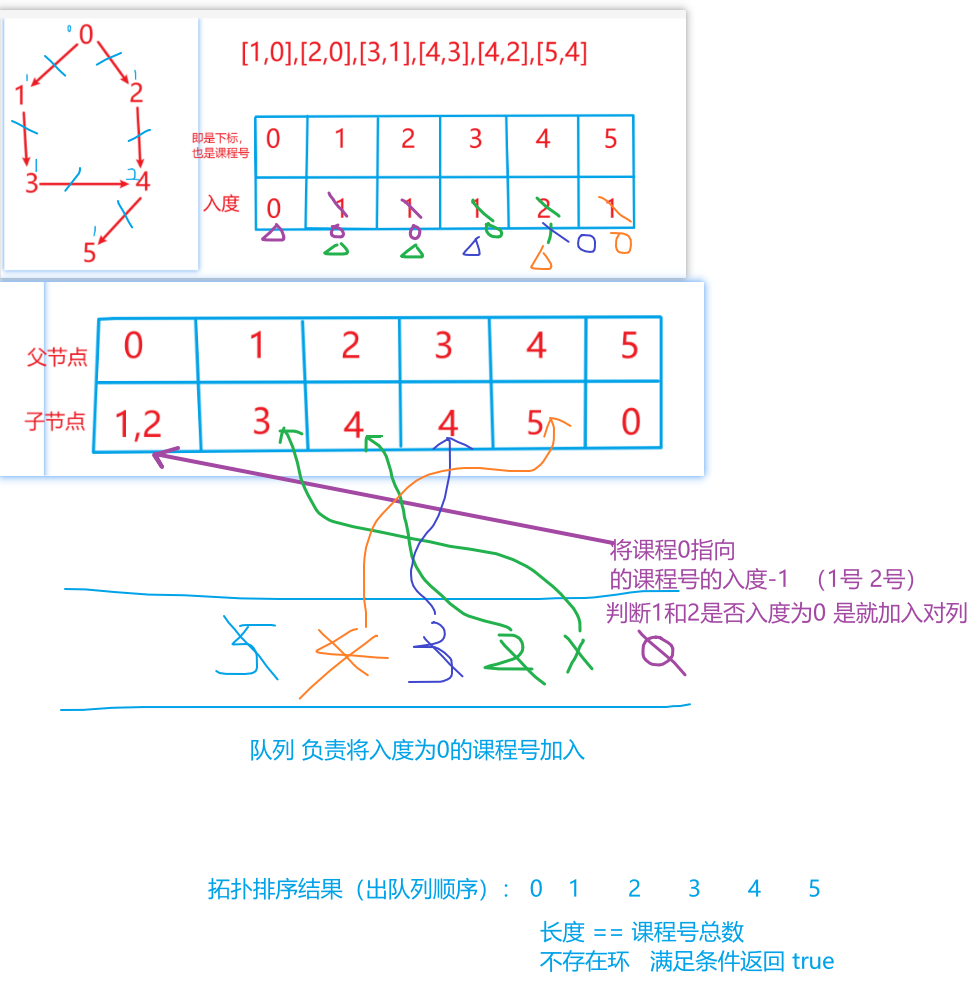
从课程号中取出入度为0的元素,加入队列中,然后根据课程号集合,将指向的课程号子集合中的课程号的入度-1,循环结束(队列为空)
-
每取出一个入度为0 的元素,就让课程号总数-1,若循环结束(队列为空),课程号总数==0,说明拓扑排序得到的排序序列 = 课程号总数 说明该有向图不存在环,也就满足题目可以完成全部课程,否则有环,就必然不可能完成
// 方法一bfs优化:
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] cous = new int[numCourses];// 构造入度数组 初始化全部位0 长度为课程数
Queue<Integer> queue = new LinkedList<>();//存放课程号入度为0的元素 入队再出队
List<List<Integer>> cousList = new ArrayList<>();//构造课程号集合,集合中每个元素同样为子集合,存储着课程号指向的课程号(记录出度指向,也就是指向元素的入度)
for(int i = 0 ;i < numCourses ; i++) // 提前给课程号集合创建空子集合
cousList.add(new ArrayList<>());
for(int[] pre : prerequisites){// 给入度数组附上 入度值,以及给课程号集合的子集合设置好出度课程和入度课程的映射
cous[pre[0]]++;
cousList.get(pre[1]).add(pre[0]);
}
for(int i = 0 ; i<numCourses ; i++){//从课程号数组中取出课程号的入度为0的元素,将课程号加入队列中
if(cous[i]==0) queue.offer(i);
}
while(!queue.isEmpty()){
int ids = queue.poll();//取出队列入度为0的元素
numCourses--;//取出一个入度为0 的元素 就让课程总数-1
for(int cur : cousList.get(ids)){// 根据入度为0 的课程号到课程号集合找到 指向的课程号集合,
if(cous[cur] >= 1) cous[cur]--;// 如果入度大于>=1将集合的课程号入度-1
if(cous[cur] == 0) queue.offer(cur); //如果入度==0 则将课程号加入到队列
}
}
if(numCourses == 0) return true;//如果numCourses--到了0 说明该课程构成的有向图 无环 满足题目所有课程都能学习
else return false;//否则不满足
}
方法二:dfs 深度优先搜索
思路:
- 将课程号数组,以下标为课程,数值初始化为0
- 构建课程号指向的课程号集合
- 寻找课程号数组值为0的课程号进行dfs深度优先
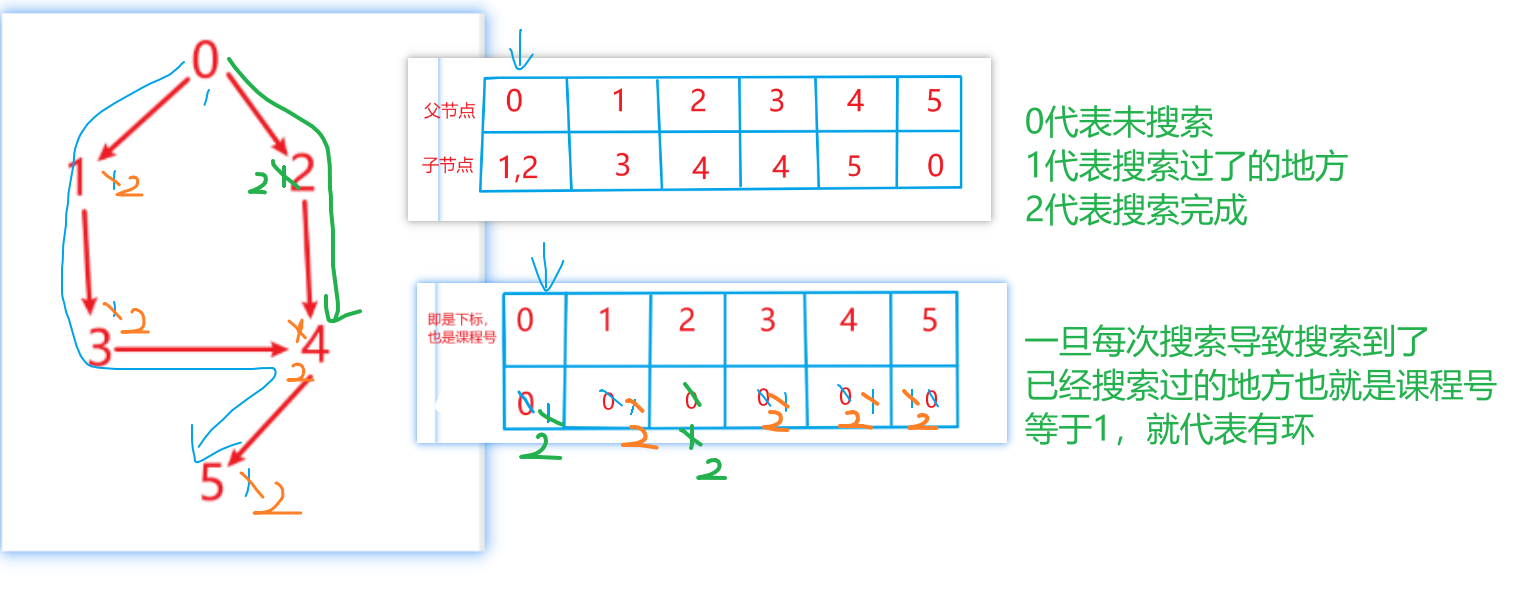
- 深度优先现将当前课程号设置为1,然后根据课程号指向的课程号集合寻找下一个课程号为0 的课程号继续dfs,dfs后判断标志位是否置为fasle了,如果是,就取反结束dfs,若不是则继续判断课程号数组的值是否为1,是就代表有环,直接返回false,最后都不满足,说明无环,将当前dfs的元素课程号的值置为2
List<List<Integer>> cousList;
int[] cous;
boolean valid = true;
public boolean canFinish(int numCourses, int[][] prerequisites) {
cous = new int[numCourses];// 构造入度数组 初始化全部位0 长度为课程数
cousList = new ArrayList<>();//构造课程号集合,集合中每个元素同样为子集合,存储着课程号指向的课程号(记录出度指向,也就是指向元素的入度)
for(int i = 0 ;i < numCourses ; i++) // 提前给课程号集合创建空子集合
cousList.add(new ArrayList<>());
for(int[] pre : prerequisites){// 给课程号集合的子集合设置好出度课程和入度课程的映射
cousList.get(pre[1]).add(pre[0]);
}
for(int i = 0 ; i<numCourses ; i++){//
if(cous[i] == 0) dfs(i); //如果是未搜索的科目,则深搜
}
return valid;
}
public void dfs(int c){
cous[c] = 1;
for(int cur : cousList.get(c)){//遍历该科目指向的学科
if(cous[cur]==0){//如果指向的某一学科未搜索过,则深搜
dfs(cur);
if(!valid){
return;
}
}else if(cous[cur]==1){//如果指向的某一学科在搜索中,则有环,标记Vaild
valid = false;
return;
}
}
cous[c]=2;//因为该科目已经完成深搜,所以标记它的状态搜索完成
}