摘要

摘要：本研究通过确定基于现实垂直风速剖面的循环可行的功率优化飞行轨迹，来研究抽水模式地面生成的空中风能系统（AWESs）的性能。这些10分钟的风速剖面来自欧洲沿海和陆地地点的中尺度天气模拟，并被纳入最优控制模型，通过优化轨迹来最大化平均循环功率。

为了降低计算成本，基于k-means聚类确定了代表性的风场条件。结果描述了在抽水周期内，风速大小和风速剖面形状对功率、牵引线张力、牵引线卷取速度和风筝轨迹的影响。通过将它们与对数风速剖面进行比较，说明了中尺度模拟风速剖面对功率曲线的影响。

在离岸地区，结果与对数风速剖面基本一致，而在陆地地区，由于更频繁的非单调风场条件，功率曲线有所不同。结果与简化的准稳态模型和风力发电机模型进行了对照。本研究还研究了基于中尺度模拟风速剖面的功率曲线如何受到参考高度选择的影响。我们的数据显示，最佳操作高度通常在400米以下，大多数AWESs在约200米左右运行。

1 引言

本研究的结构如下所示：

第2节介绍了中尺度WRF模型，分析了离岸和陆地风资源，引入了k-means聚类算法，并总结了聚类风矢量的结果。

第3节介绍了动态AWES模型，包括飞行器和牵引线模型，以及地面站约束条件。

第4节描述了AWEBox优化工具箱，并总结了飞行器参数、系统约束和初始条件。然后，介绍了Sect. 5中的WT和AWES参考模型。

第6节中呈现的结果包括各种性能参数的飞行轨迹和时间序列数据，以及牵引线长度、操作高度和功率曲线估算的统计分析。

第7节总结了研究结果，并提出了未来工作的展望和动力。

2. 风力条件

2.2 风况

图2 在模拟年期间，普里茨沃克（陆上）和FINO3（海上）100和500米高度的年度风向和速度统计的风玫瑰图。

图3. 对比了WRF模拟的每个高度层的年度风速U概率分布，高度范围为1000米，分别是陆地上（a）和离岸（b）。非线性的颜色方案表示低海拔地区，尤其是陆地上，具有高概率，同时仍然区分了较高海拔处的较低、分布广泛的频率。

中性分层大约占两个地点一年约20%的时间。陆地表面的热容较低，导致更快的热传递和更快的地表冷却，这有利于稳定层化的发展（约17%在陆地上，约6%在离岸）。离岸位置具有更高的不稳定条件的概率，这可能是由于与上方空气相比，海洋表面温度较暖所引起的（Archer等人，2016年）。

图4. 代表性的风速剖面 $U^{\prime }$ 在其原始方向上以及旋转后，使得结果剖面U的主要风向指向x方向。面板（a）显示顶视图，面板（b）显示前视图，面板（c）显示侧视图，面板（d）显示等距视图。主要风向由平均风矢量U(zref)（黑色）和U(zref)（蓝色）定义，位于100至400米之间（虚线）。例如，在 z = 150米处的风矢量（红色）（a, d）被分解为u和v（b, c）。

无论是不稳定条件还是稳定条件，都可以导致非对数和非单调的风速（U）剖面。不稳定条件通常伴随着几乎均匀的U剖面，这是由于增加的混合作用，而夜间稳定的陆地边界层可能会出现低层急流（LLJs）（Banta，2008）。两个地点都存在高概率的未分类条件（标记为“其他”），这些条件大多与低风速相关。

2.3 风况聚类

近地表大气的稳定性通常是用来描述近地表大气的一种接受的方法，通常由奥布霍夫长度（Obukhov length）来量化（Obukhov, 1971; Sempreviva and Gryning, 1996），它仅使用地表数据（第2.2节和等式1）。之前的研究（Sommerfeld等，2019a, b）表明，奥布霍夫长度分类的风速剖面U随着高度的增加会发生分歧，特别是在中性和稳定条件下。这表明大气稳定性在垂直方向上是不均匀的，暗示基于地表的稳定性分类对于较高高度是不足够的。与根据大气稳定性分类风场不同，后者需要额外的温度和热通量数据，聚类只使用多个高度的风速数据来将风速剖面按相似性分组。这导致更具凝聚力的剖面组（Schelbergen等，2020）。因此，聚类也可以应用于仅包括风速测量的数据，比如激光雷达（lidar）数据。

本研究中使用的k-means聚类算法（Pedregosa等，2011）之所以选择，是因为它易于使用且在数据集维度较高的情况下具有可扩展性。许多其他算法也可以产生类似的结果，但在本研究范围之内不会对聚类算法进行比较。风速剖面$U^{\prime }$（图4，黑色）被旋转，以使主要风分量U(zref) =U(100m≤ z ≤ 400m)指向正x方向 U（蓝色），以消除方向依赖性。每个高度层的速度分量被分解为主要风向的u分量和与之垂直的v分量（红色）。风速剖面U没有显示。这导致了更均匀的聚类，并简化了风速数据和AWEBox结果的比较。这类似于假设全向操作。

高达1000米的风速数据包括30个高度层和两个方向的数据点。聚类算法将每个数据点分配给其中一个由其各自的簇均值（也称为质心）表示的k个簇之一。这些质心被选择以最小化到每个簇内每个数据点的欧几里德距离之和。这个成本函数也被称为惯性或簇内平方和。因此，质心通常不是实际的数据点，而是簇的平均值，最多只会偶然与数据点重合。簇标签是随机初始化的结果，没有数学意义。因此，在接下来的第2.4节中，我们通过平均U(zref)在100-400m之间对聚类进行排序和标记，以进行后续分析。变量k指的是固定和预定义的簇数。k 的选择会显著影响风资源描述的准确性以及计算成本。k 的选择是根据 “拐点法” 和轮廓系数来确定的。 “拐点”（曲线的拐点）是表明底层模型适用于相应数量簇的一个良好指示。

k可以选择在惯性减小变得极小或线性减小的点上（Pedregosa等，2011）。

图5. 关于聚类数k的k-means聚类惯性（a），包括垂直陆地（蓝色）和离岸（橙色）风速剖面U长达1000米的1年数据。垂直陆地（b）和离岸（d）的轮廓系数表达到相邻聚类的距离，并根据在高度100至400米之间的平均U(zref)进行颜色编码，与图6、9、10和11相同。虚线红线代表轮廓得分，即平均轮廓系数。轮廓得分（c）随着聚类数k的变化，适用于两个地点。聚类数k = 10仅用于展示目的。在“结果与讨论”部分中，分析采用k = 20个聚类。

图6. 垂直陆地上（a, c）和离岸（b, d）的平均年度风速剖面（质心），通过k-means聚类得到k = 10（a, b）。所有WRF模拟的风速剖面U均以灰色表示。这些质心根据在高度100至400米之间的平均U(zref)的升序排序、标记和着色。每个聚类C的相应聚类发生频率 f 在（c）和（d）下方显示。

惯性的绝对值（图5a）不是标准化的度量，它随着所考虑数据集的大小而变化。另一方面，轮廓系数（图5b和d）在-1（最差）和1（最佳）之间标准化。它们表示数据点与其簇的成员关系，与其他簇进行比较，即一个簇中每个数据点与相邻簇中的数据点的接近程度（Pedregosa等，2011）。负值表明数据点可能被分配到错误的簇。轮廓分数，由虚线红色垂直线表示，是对于固定数量的簇 k 的所有轮廓系数的平均值。出于可视化目的，选择了k = 10个簇。每个簇根据在100到400m之间的平均U(zref)进行排序和着色，颜色与图6中相同。对于多个k进行这些轮廓系数分析，得到了图5c所示的趋势。k值为20似乎是可用数据集的不错选择，因为对于更多簇的惯性减小仅是适度的，表明额外的计算成本可能不值得。同样，轮廓分数在更多簇的情况下几乎保持不变。因此，k = 20已被选择用于第6节的分析。

图7. 使用k-means聚类算法对垂直陆地上的U进行分类。第6节中的分析采用k = 20个聚类。这里选择k = 10仅用于可视化目的。平均轮廓（质心）以蓝色显示，与该聚类相关的轮廓以灰色显示。聚类1到10（a-j）按照在100到400米之间的平均质心U(zref)升序排序并标记。每个聚类C的相应聚类频率f在图6中显示。用红线突出显示了优化工具箱实施的U。

2.4 聚类分析

出于可视化目的，以下小节仅使用k = 10个簇来描述两个位置的风场条件。在“结果和讨论”部分（第6节）中的分析使用k = 20个簇。

图6a和b显示了聚类风速剖面U的平均值，也称为质心。它们的颜色对应于在100到400米高度范围内的平均U(zref)。所有WRF模拟的U都以灰色表示。簇概率（图6c和d）按照在考虑的高度范围内的平均质心速度进行排序，其颜色和标签（C = 1–10）表示。

如预期的那样，离岸的U（图6b）在低高度上较高，风切变较低，而在岸的情况则相反（图6a）。总的来说，离岸的质心更加单调，因为它们没有明显的U峰值（即，LLJs），并且在岸上获得了比离岸更高的最大风速。每个簇内的U剖面涵盖了一个相对较小的范围，表明了一致的簇。图7（陆地）和图8显示了每个簇内U的分布。在两个位置，前两个簇（图7a，b和图8a，b）表现出非常低的风切变，200米以上的风速低而几乎恒定。这些低风速簇在陆地上约占25%（图6c），在离岸上约占20%（图6d），如相应的簇频率f所示。标准的对数风速剖面不能准确描述这种几乎恒定的剖面，这可能导致在较高海拔处对U的过高估计。AWESs必须要么能够在低风速下运行，要么能够安全地自主降落和起飞。陆地上的簇4和5（图7d，e和图8d，e）似乎主要由非单调剖面组成，因为这些质心在大约200米和300米处显示出明显的LLJ鼻子。离岸的簇7和8（图7g，h和图8g，h）在较高高度也显示出轻微的风切变反转。

簇C = 1（a）到C = 10（j）根据U(zref = 100–400 m)之间的平均质心（蓝线）风速进行排序。红线表示与每个簇内U(zref)的第5、50和95百分位数相关联的剖面。为了减少计算成本，仅这些剖面后来被实现到AWEBox优化工具箱中。我们选择了这些剖面，因为它们不太可能是簇的极值的不规则离群值，同时仍然代表了其各自簇内的变化。这些剖面说明了它们各自簇内的变化，并不像簇的质心或缩放或半经验逼近，如对数风速剖面那样是平均剖面。显然，风速大小在聚类过程中起主导作用。通过在对数据进行聚类之前对其进行标准化，可以实现更清晰的风速剖面形状区分（Molina-García等，2019；Schelbergen等，2020）。

2.5 聚类统计分析

这个小节探讨了簇与月度、日变化和大气稳定性之间的关系。这些分析揭示了风场和AWES性能变化的模式。随后的小节将使用k = 20个簇的风数据，而在这里只选择k = 10个簇用于展示目的。簇按照平均质心风速U(zref = 100–400 m)的升序排序，并使用与图5和图6相同的颜色编码。

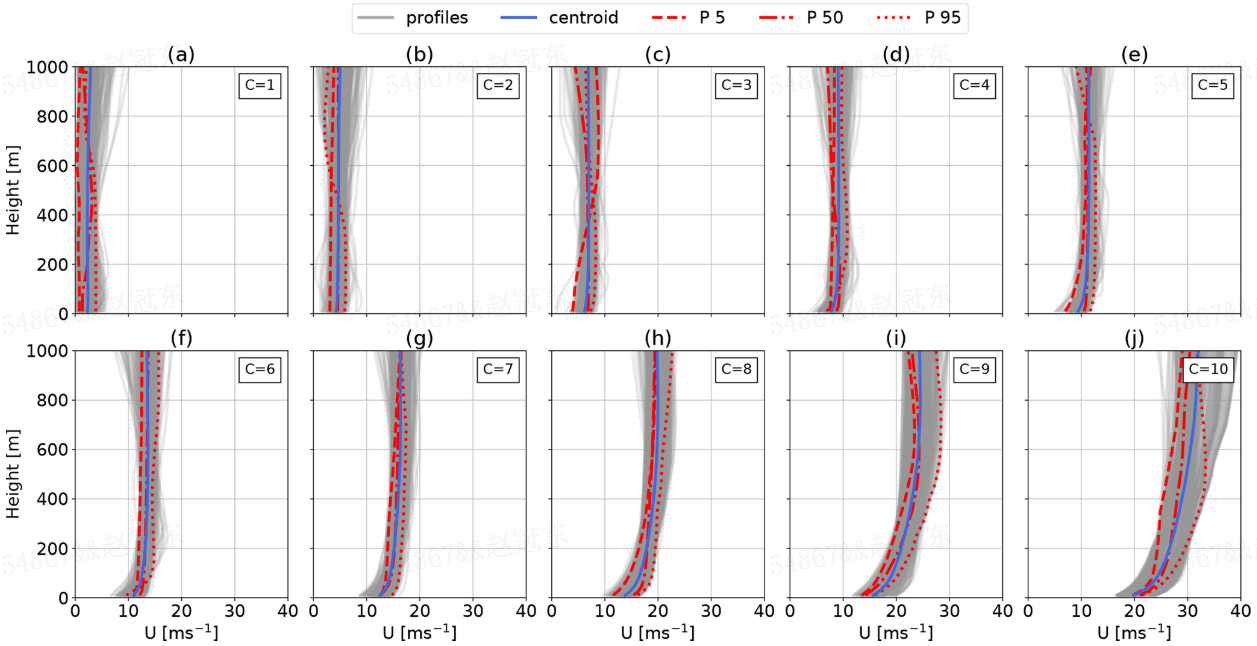
图8 显示了使用k-means聚类算法对离岸风速剖面进行分类。在第6节的分析中使用了k = 20个簇。这里选择k = 10只是为了可视化的目的。平均剖面（质心）以蓝色显示，与该簇相关的剖面以灰色显示。簇1到10（a-j）按照在100到400米之间的平均质心U(zref)的升序排序和标记。每个簇C的相应簇频率f在图6中显示。通过红线突出显示了优化工具箱实施的U。

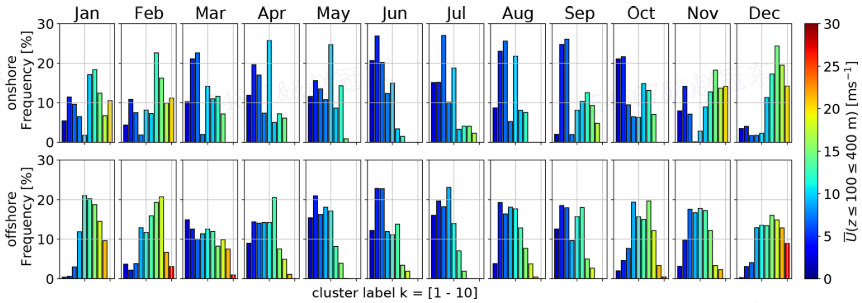
图9

如图9所示，两个位置都表现出明显的年度模式。高风速在冬季更为常见，而夏季更常见低风速。这可能是由于地表加热的季节差异和大气混合的差异所致。与最高风速相关的两个陆地和离岸簇几乎仅在11月至2月期间存在。

离岸数据表明，如图10所示，白天只有略微增加低风速簇的频率，几乎没有显著的昼夜变化。另一方面，陆地簇更依赖于昼夜周期，日出后低速簇的可能性较高。包括LLJ鼻子（图6）的陆地簇4的频率在白天几乎降至零，夜晚升高，支持这一簇与夜间LLJs有关的观点。

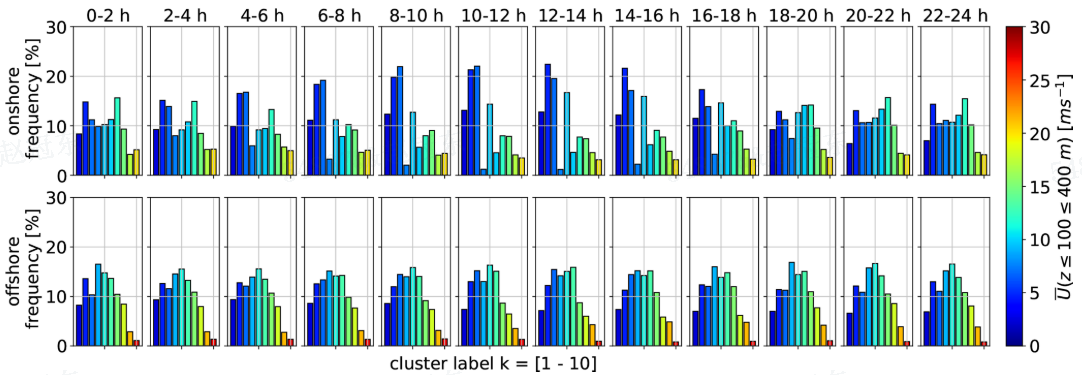
图10

风速簇（图11）与大气稳定性相关。低风速簇占年度风资源的约20%到30%。这些簇的Obukhov长度接近零（可能是由于非常低的摩擦速度u∗引起的），根据Floors等人（2011）的分类被归类为“其他”（表2）。不稳定（U）和近不稳定（NU）条件与稍高的风速相关。最高风速发生在中性（N）和近稳定（NS）条件下。应该承认，由大气压力梯度驱动的强风可以导致中性分层。与陆地簇4相关的LLJ剖面最有可能在稳定（S）和非常稳定（VS）的条件下发展。

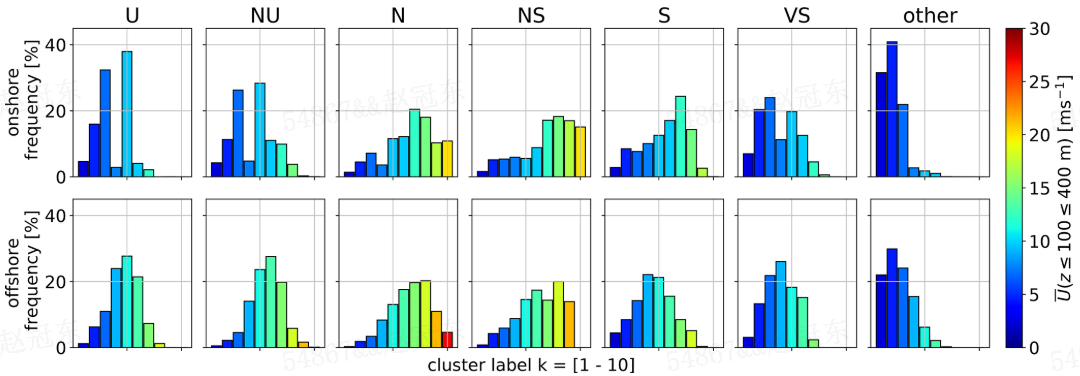
图11

总之，k-means聚类可以有效地将具有相似特征的风速剖面分组，直到较高的高度。这些簇与季节性和昼夜变化以及大气稳定性相关。风速剖面的大小似乎对产生的簇的影响大于剖面的形状。该算法能够识别不常见的非单调剖面形状，包括具有LLJs的剖面。在进行聚类之前对剖面进行归一化可以提供有关垂直剖面不同形状的更多信息，但本研究未进行此操作。

3 引言

图13. 显示了由Makani（红色方案）（Echeverri等，2020）和Ampyx Power（蓝色方案）（Ampyx Power BV，2020；Kruijff和Ruiterkamp，2018）提供的实际发布（圆形）和预期（方形）的飞机质量缩放数据。菱形数据（绿色方案）表示在研究论文中使用的Ampyx Power原型的放大版本的质量（Haas等，2019；Eijkelhof等，2020；van Hagen等，2023）。对于大多数数据，质量与缩放指数κ在2.2至2.6之间（灰色区域）。所选的质量缩放指数κ = 2.4由虚线表示，并且调查的缩放AP2设计由红色X标出。