目录

题目：

示例：

分析：

代码：

---

题目：

示例：

分析：

题目给我们一棵搜索二叉树，要我们将这棵二叉树转变为字符串，同时我们需要根据字符串再变回二叉树，具体的方法我们可以自行制定。

这道题让我想起了力扣的另外一道题：

我们可以把二叉树的前序遍历和中序遍历的结果压缩成字符串。

要由字符串变为二叉树的时候，可以通过字符串分割出前序遍历和中序遍历，再通过前序与中序遍历序列构造二叉树。

因此我们今天的重点放在这道105题上。

我们应该如何通过前序遍历的结果和中序遍历的结果来构造二叉树？

我们先看看两者的结果分别有什么特点。

我们知道，前序遍历和中序遍历对于二叉树的遍历顺序是一样的，都是先遍历左子树再遍历右子树，不一样的是，取节点值的时机不同，前序遍历是在一开始就去了当前节点的值，而中序遍历是在递归遍历完了当前节点的左子树之后才取的值。

因此前序遍历的结果的值的顺序就是我们递归二叉树的顺序，因为前序遍历一递归到节点就取值，因此前序遍历的第一个元素一定是根节点。

而中序遍历，用我的话来说，就是把二叉树压扁，说起来比较抽象。可以参考下面的动图看一看。

因为二叉树压扁之后就是中序遍历的结果，所以结果里某个节点的左边的节点，都在这个节点的左子树上，在这节点右边的节点，都在这个节点的右子树上。

大概懂了两种遍历结果的特点之后，我们来分析如何通过这俩结果来构造一棵二叉树。

我们就以105题的示例一为例。        

中序遍历的结果是:

[ 9 , 3 , 15 , 20 , 7]

前序遍历的结果是：

[ 3 , 9 , 20 , 15 , 7 ]

根据我们刚才说的，前序遍历的结果的第一个元素就是根节点。因此我们构造出的二叉树的根节点的值就是前序遍历的第一个值：3。

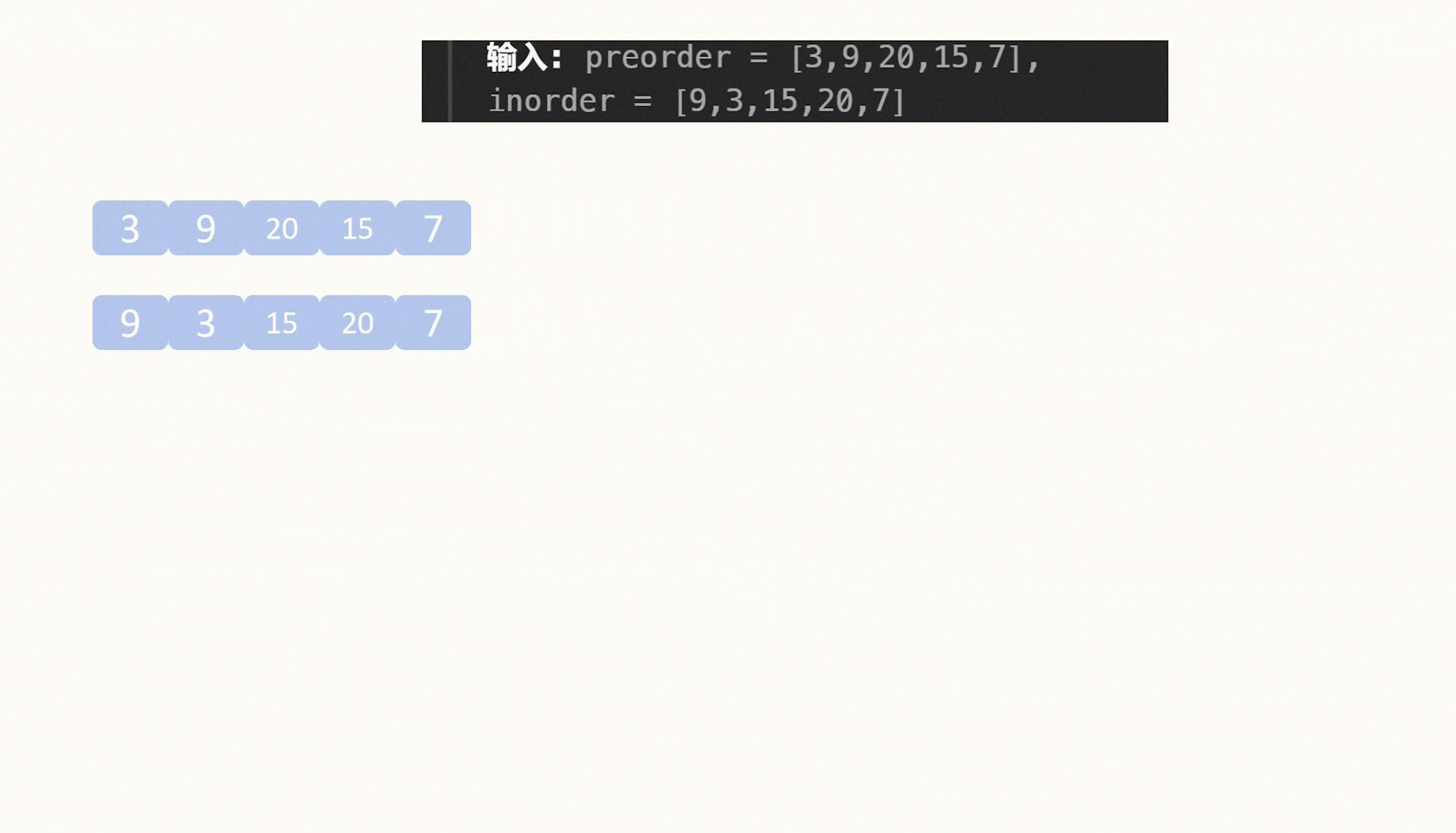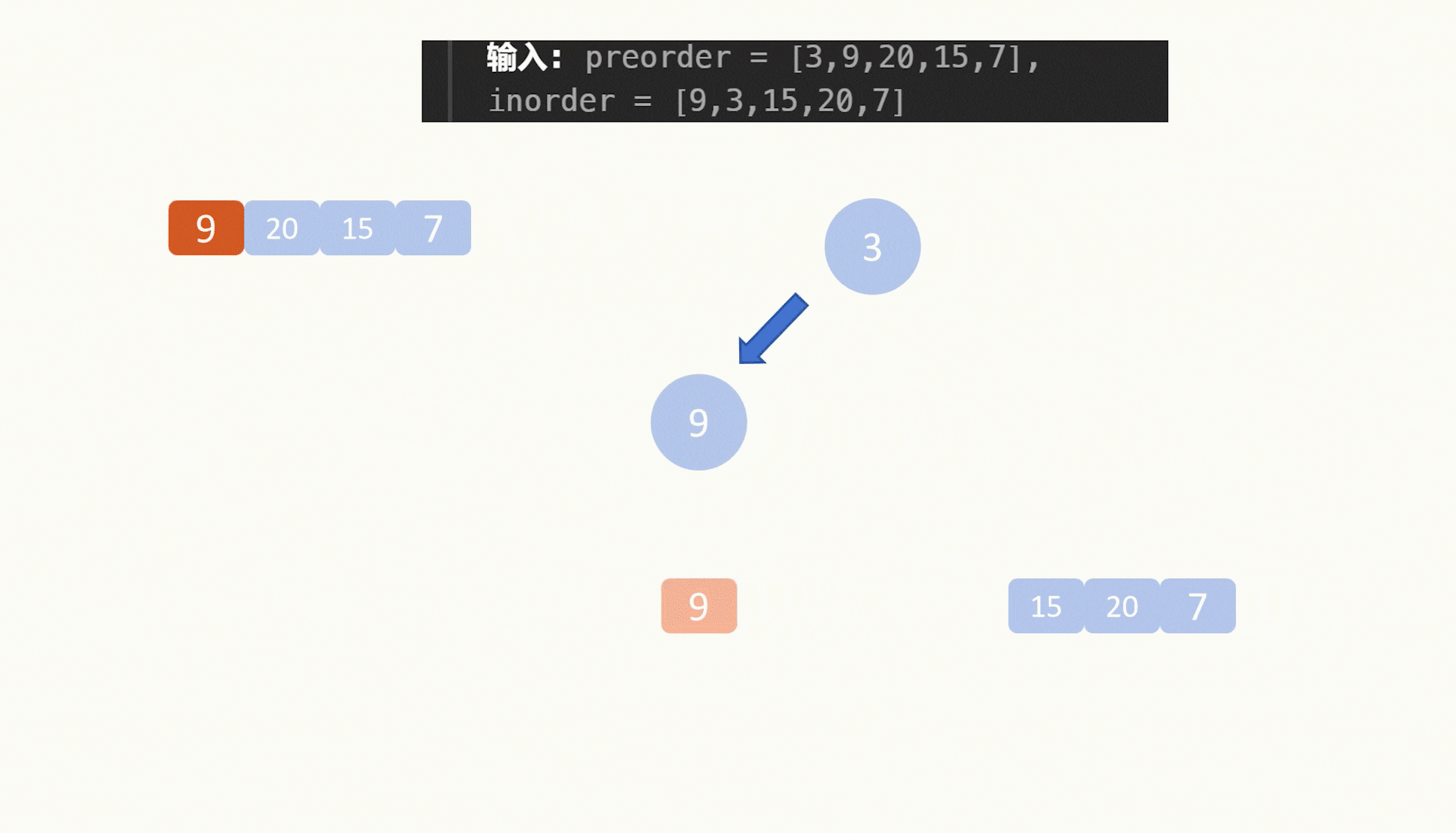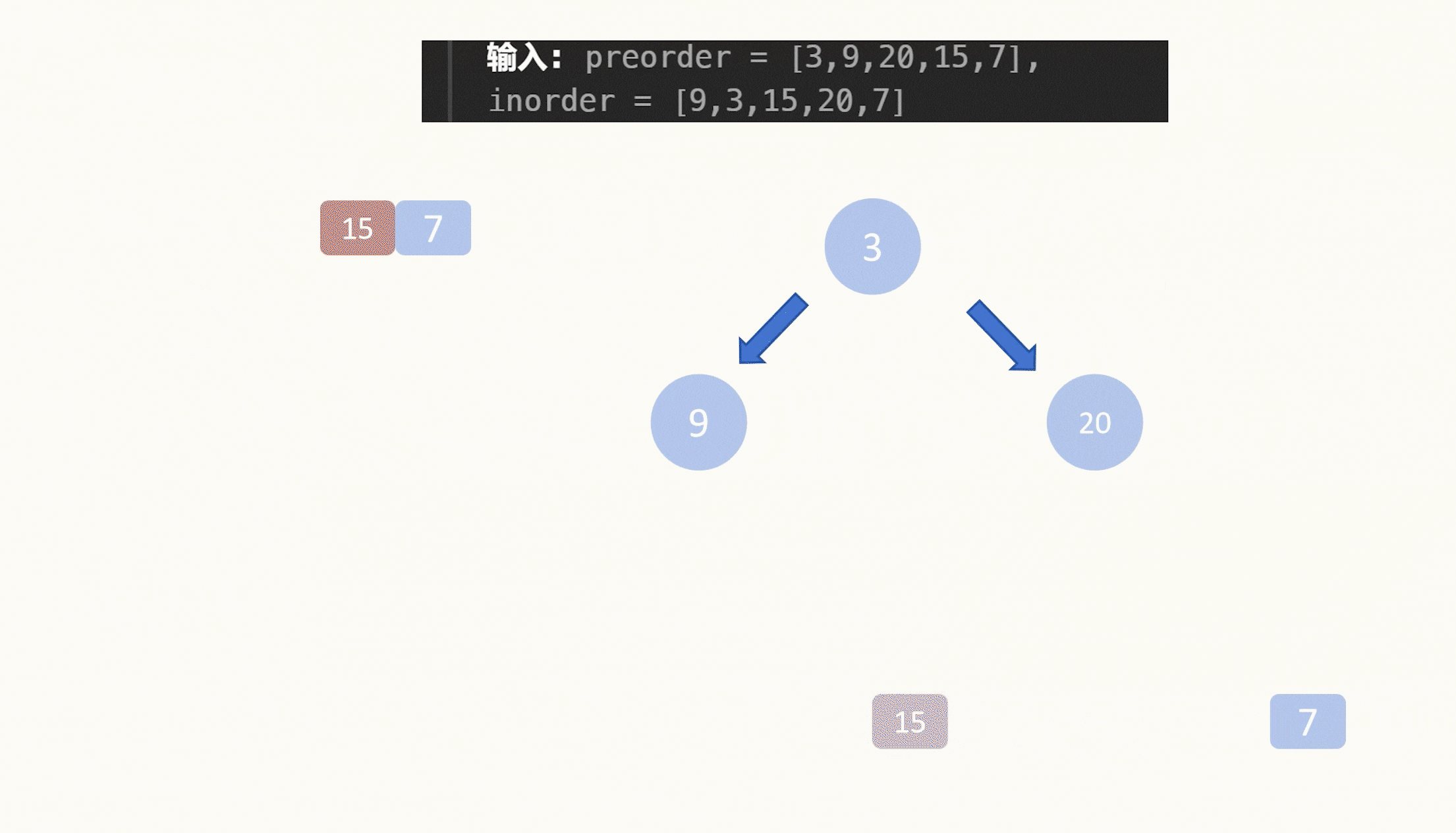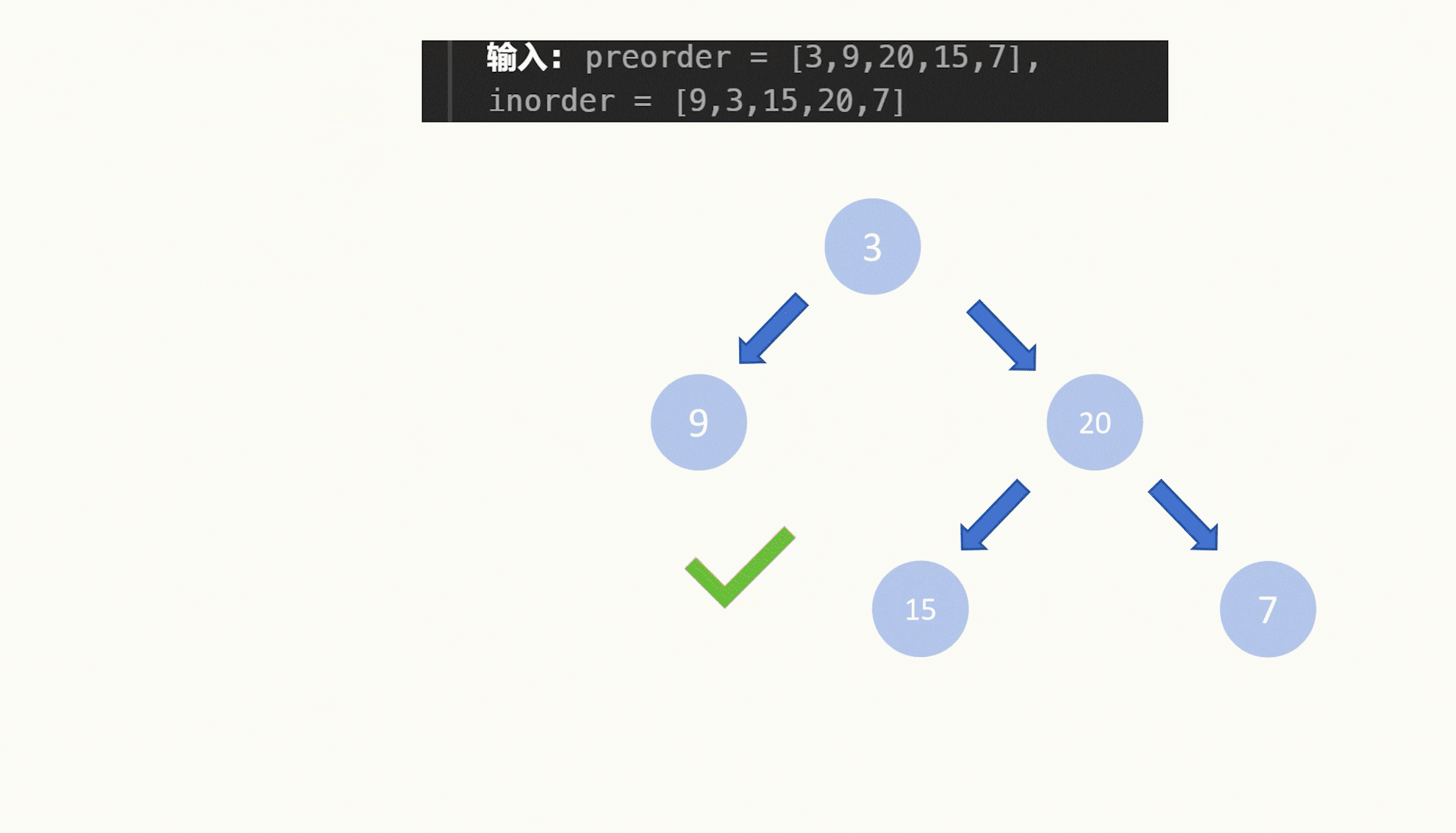
而3在中序遍历中，将结果分为了两半，【9】和【15,20,7】。

又根据我们刚才说的，【9】在原本3的左边，所以9在3的左子树，【15,20,7】在3的右边，所以它们仨在3的右子树上。

3的左子树就9一个节点，所以我们可以知道根节点的左子树节点的值就是9，那么问题在于右子树节点的值，有三个备选的值都在右子树上，那么哪一个值是根节点的右子树的根节点的值呢？

这时候我们就需要看前序遍历了，按照顺序来看，开头的3和9我们都用过了，那么接下来轮到的是20，所以根节点的右子树节点的值就是20。

20在中序遍历中，将剩余的结果又分为了两半，是15和7，分别是20的左右子树。至此遍历完毕，我们也就构造完了二叉树。

我们知道如何用前序遍历和中序遍历的结果构造二叉树之后我们再回过头来看看今天的每日一题。

前序遍历和中序遍历相信大家都懂，我们先分别将两个结果集的每个元素之间用一个特殊符号来连接起来，代码中我用的是‘#’，再用另一个特殊符号来连接两个结果集，代码中我用的是‘/’。如此我们就将一棵二叉树序列化了。

反序列化的话，我们只需将前序遍历的结果和中序遍历的结果从序列化后的字符串中提取出来，然后直接使用105题的代码就可以，我在代码中也是这么做的。

我这种做法没有利用到搜索二叉树的特性，并且代码又臭又长，所以仅供大家参考，提供一种思路，可以参考下面的动图来体会一下怎么通过前序和中序遍历来构造二叉树。

代码：

class Codec {
public:
    vector<int>cache;
    void qianxv(TreeNode* root){    //前序遍历
        if(root==nullptr) return;
        cache.push_back(root->val);
        qianxv(root->left);
        qianxv(root->right);
    }
    void zhongxv(TreeNode* root){   //中序遍历
        if(root==nullptr) return;
        zhongxv(root->left);
        cache.push_back(root->val);
        zhongxv(root->right);
    }
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {  
        //将前序和中序的结果拼接
        cache.clear();
        qianxv(root);
        string res="";
        for(auto c:cache) res+="#"+to_string(c);
        res+='/';   //中间用'/'分隔
        cache.clear();
        zhongxv(root);
        for(auto c:cache) res+="#"+to_string(c);
        return res;
    }

    //力扣105题,前序与中序构造二叉树
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(inorder.size()==0) return nullptr;
        TreeNode* res=new TreeNode(preorder[0]);    //根节点一定是前序遍历的第一个
        int index=0;
        for(;index<inorder.size();index++){
            if(inorder[index]==preorder[0]) break;  //找到根节点在中序遍历的位置
        }   
        preorder.erase(preorder.begin());   //移除前序遍历第一个节点
        vector<int>left,right;
        //中序遍历的位置的左边是当前节点的左子树
        if(index!=0) left=vector<int>(inorder.begin(),inorder.begin()+index);
        //中序遍历的位置的右边是当前节点的右子树  
        if(index!=inorder.size()-1) right=vector<int>(inorder.begin()+index+1,inorder.end());
        //传入更新过的前序遍历和中序遍历来构造左右子树
        res->left=buildTree(preorder,left);
        res->right=buildTree(preorder,right);
        return res;
    }
    
    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        vector<int>preorder,inorder;
        int index=0;
        while(data[index]!='/'){
            if(data[index]=='#'){
                string temp="";
                index++;
                while(data[index]!='#'&&data[index]!='/'){
                    temp+=data[index];
                    index++;
                }
                preorder.push_back(stoi(temp));
            }
        }
        index++;
        while(index<data.size()){
            if(data[index]=='#'){
                string temp="";
                index++;
                while(index<data.size()&&data[index]!='#'){
                    temp+=data[index];
                    index++;
                }
                inorder.push_back(stoi(temp));
            }
        }
        return buildTree(preorder,inorder);
    }
};