迷宫问题是比较经典的算法问题，一般可以用动态规划、回溯等方法进行解题，这道题目是我昨晚不同路径这道题趁热打铁继续做的，思路与原题差不多，只是有需要注意细节的地方，那么话不多说，直接上coding和解析！

题目描述

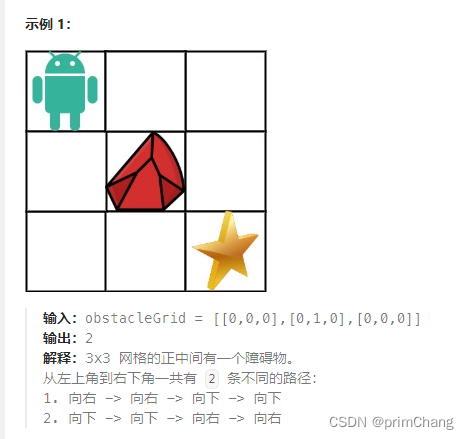
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

解析

如果做过类似迷宫问题的读者，对于这道题目的思路想必也会第一时间想到仍然使用动态规划的思路去解答，但是对于路径中的障碍物在这里却需要着重的单独讨论，因为有了障碍物，那么对于部分目标点的路径数会发生改变。此题目中需要考虑的特殊位置有如下图所示；

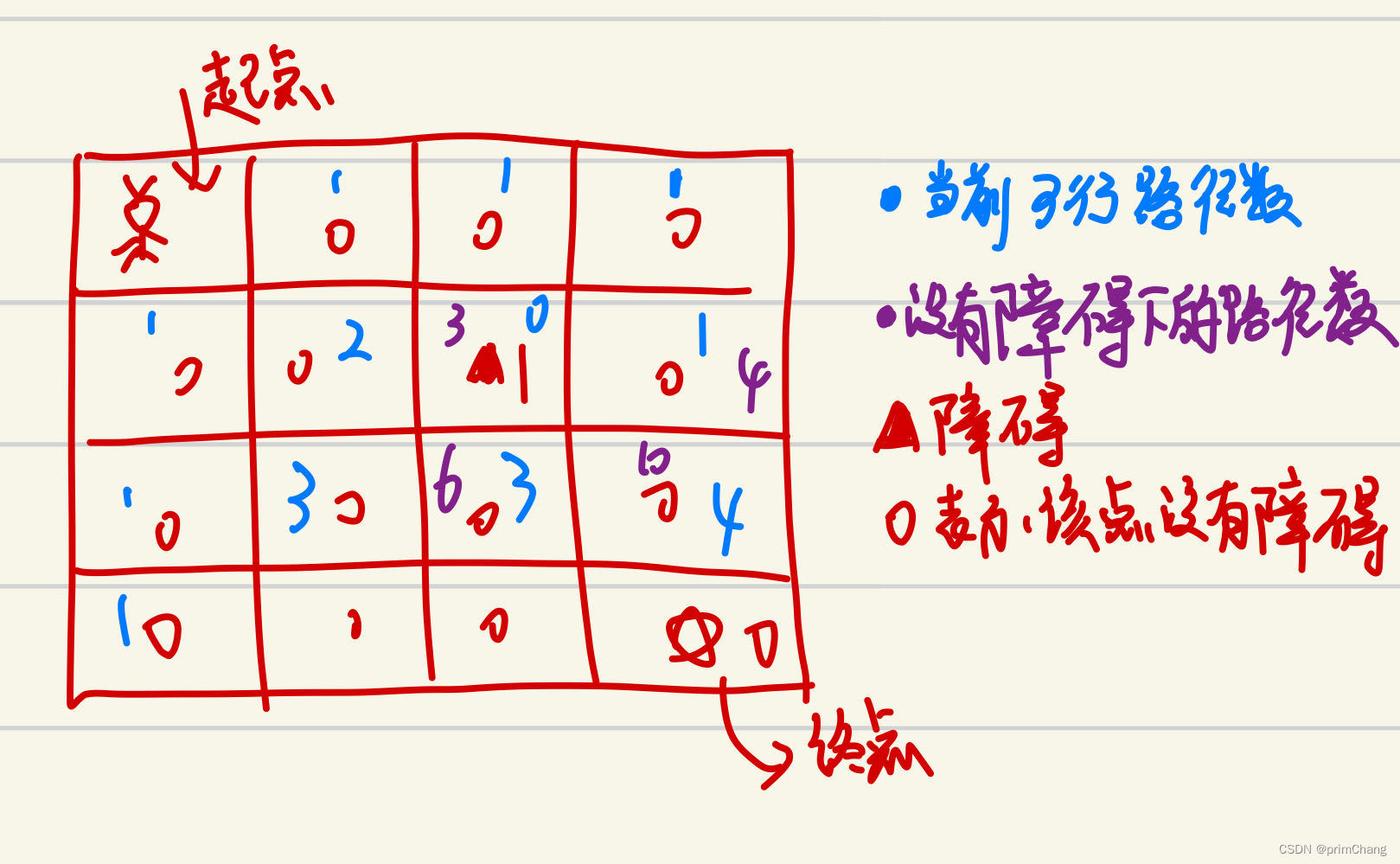
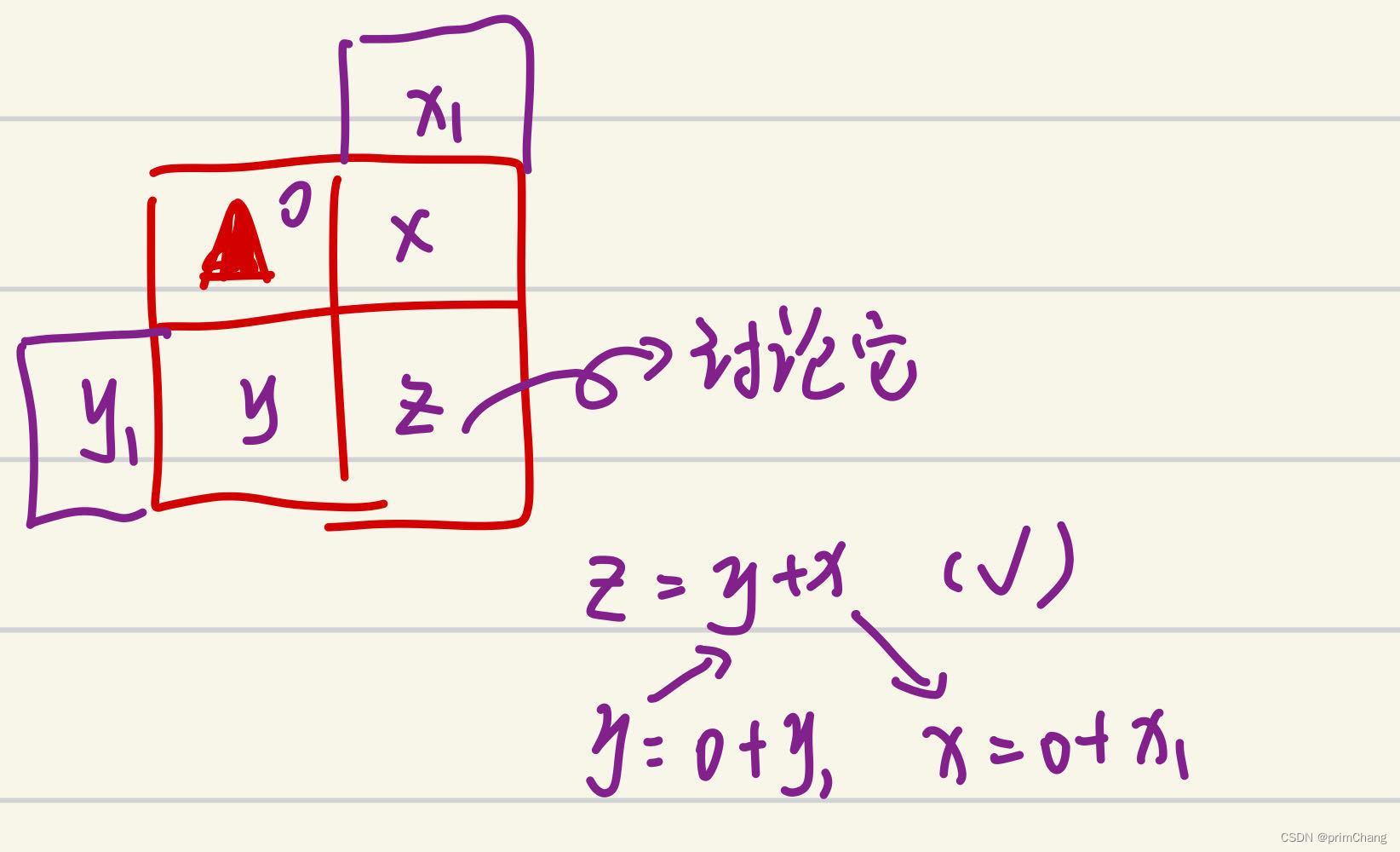
所画图给出了一种情况下的各个点下的路径数，可以看到，对于紫色笔给出的新的当前的节点路径数，仍满足原始状态下的dp[i][j] = dp[i-1][j]+dp[i][j-1]的动态递推式（但对于有障碍的节点不满足，那么障碍节点可达到路径数直接为0），对于迷宫问题，当前节点的可通行路线是由当前节点的左侧节点和正上方节点的可通过路径数相加得到，那对于左上方存在障碍的情况，当前节点的可通过数就需要变化。如下图所示。

这是相对于原始题目的第一处变化，考虑了障碍物，那么就得讨论一下障碍物在某些特殊位置下的特殊情况，比如障碍物在初始行、列上的时候，比如：

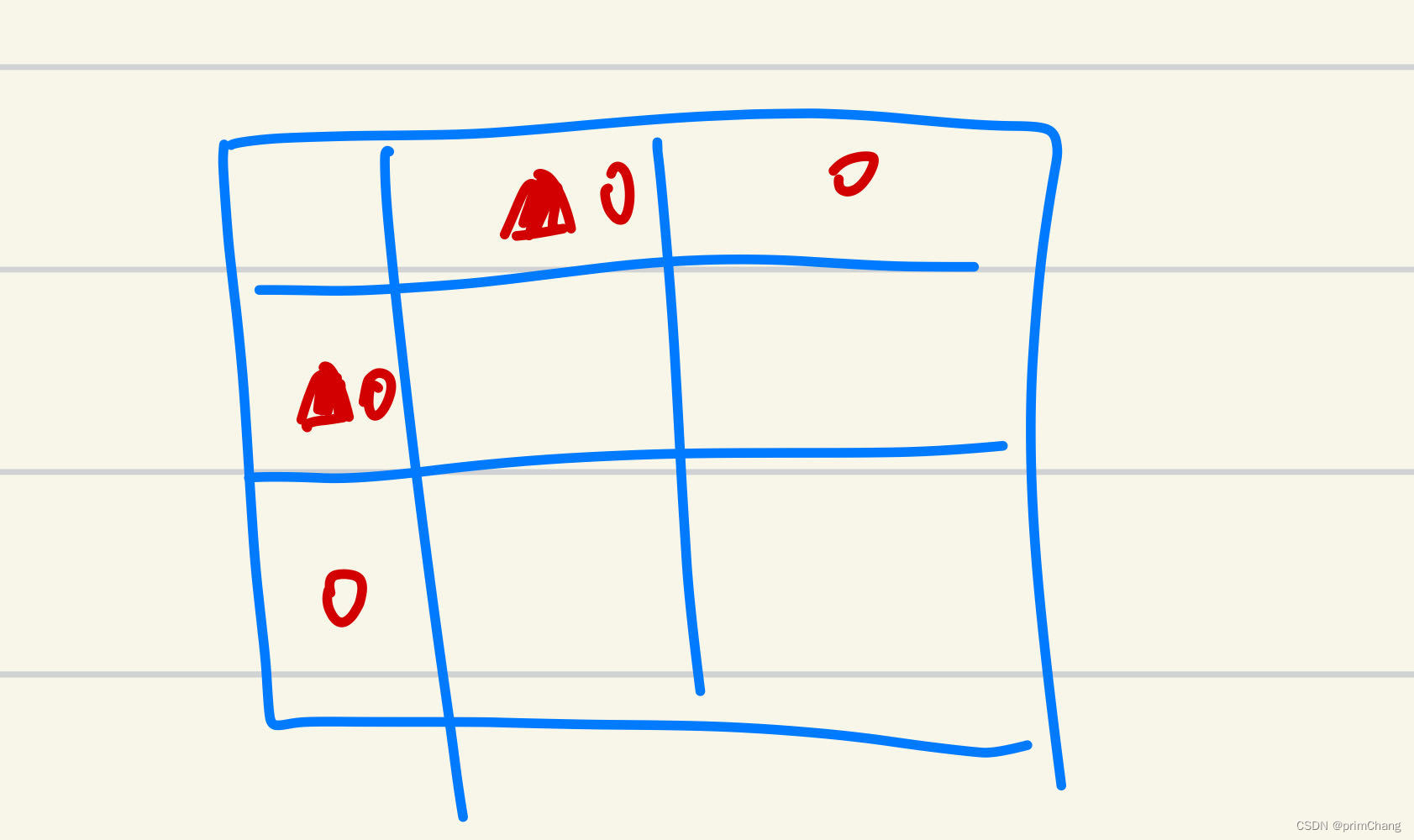
这种情况下，我们就不能单纯的只能把障碍物所处的位置上的路径数置为0，而是要把往后的那一列/一行上的数据都要置为0，为什么，因为机器人只能向下或者向右走，所以，对于初始行、列上的障碍物往后的点，机器人是无法到达的！！！
当然，还剩下最后一个情况，起点就有障碍物，那直接return 0咯~

代码

1.初始化dp数组

//初始化dp数组，我这里全给的-1，方便后续判别障碍物、无障碍物和路径数
int dp[110][110];
        for(int i=0;i<110;i++){
            for(int j =0;j<110;j++){
                dp[i][j] = -1;
            }
        }

2.根据地图，将地图中障碍物所处对应的dp数组位置置路径数为0

for(int i=0;i<obstacleGrid.size();i++){
            for(int j=0;j<obstacleGrid[i].size();j++){
                if(i == 0 && j ==0){//起点是障碍物
                    if(obstacleGrid[i][j] == 1){
                        return 0;
                    }
                }
                if(i == 0){//障碍物在初始行上
                    if(obstacleGrid[i][j] == 1){
                        for(int m = j;m<obstacleGrid[i].size();m++){
                            dp[i][m] = 0;
                        }
                    }
                }
                if(j == 0){//障碍物在初始列上
                    if(obstacleGrid[i][j] == 1){
                        dp[i][j] = 0;
                        for(int x = i+1;x<obstacleGrid.size();x++){
                            dp[x][j] = 0;
                        }
                    }
                }else if(i != 0 && j!= 0){//障碍物不在特殊位置上，那直接对应位置dp设置为0即可
                    if(obstacleGrid[i][j] == 1){
                        dp[i][j] = 0;
                    }
                }
            }
        }

3.计算dp数组

for(int i=0;i<obstacleGrid.size();i++){
            for(int j=0;j<obstacleGrid[i].size();j++){
                if(i == 0 || j == 0){
                    if(dp[i][j] == -1){
                        dp[i][j] = 1;
                    }
                }if(i != 0 && j != 0){
                    if(dp[i][j] != 0){
                        dp[i][j] = dp[i-1][j] + dp[i][j-1];
                    }
                }
            }
        }

4. 完整代码和结果

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        // 跟第一种情况是一样的，只是对于地图中有障碍物的地方，对应的dp数组置为1
        int dp[110][110];
        for(int i=0;i<110;i++){
            for(int j =0;j<110;j++){
                dp[i][j] = -1;
            }
        }
        for(int i=0;i<obstacleGrid.size();i++){
            for(int j=0;j<obstacleGrid[i].size();j++){
                if(i == 0 && j ==0){
                    if(obstacleGrid[i][j] == 1){
                        return 0;
                    }
                }
                if(i == 0){
                    if(obstacleGrid[i][j] == 1){
                        for(int m = j;m<obstacleGrid[i].size();m++){
                            dp[i][m] = 0;
                        }
                        // break;
                    }
                }
                if(j == 0){
                    if(obstacleGrid[i][j] == 1){
                        dp[i][j] = 0;
                        for(int x = i+1;x<obstacleGrid.size();x++){
                            dp[x][j] = 0;
                        }
                        // break;
                    }
                }else if(i != 0 && j!= 0){
                    if(obstacleGrid[i][j] == 1){
                        dp[i][j] = 0;
                    }
                }
            }
        }
        for(int i=0;i<obstacleGrid.size();i++){
            for(int j=0;j<obstacleGrid[i].size();j++){
                if(i == 0 || j == 0){
                    if(dp[i][j] == -1){
                        dp[i][j] = 1;
                    }
                }if(i != 0 && j != 0){
                    if(dp[i][j] != 0){
                        dp[i][j] = dp[i-1][j] + dp[i][j-1];
                    }
                }
                // else{
                //     dp[i][j] = dp[i-1][j] + dp[i][j-1];
                // }
            }
        }
        cout<<dp[obstacleGrid.size()-1][obstacleGrid[0].size()-1];
        return dp[obstacleGrid.size()-1][obstacleGrid[0].size()-1];
    }
};

总结

个人感觉，这类题目是十分具有代表性的动态规划算法题 ，为什么这么说，因为动态规划要满足最优子结构，而恰恰这类题的子结构十分清晰，就比如我要知道当前位置有几种路径可以到达，就可以直接从我的前一步，也就是我的左边那一步和正上面的那一步就能到达，也就是我的左边和上面是与我当前可联通的，那么就直接得到了我当前的可通行路径数。有的人可能会说，那这样的话，应该是两者之和再加1才是最终的路径数呀？
其实不然，我最开始也陷入了这样的思维模式中去了，而其实应该这么想，我们所要求的是路径，而不是步数，讨论的不是走了几步，而是有几种到达的方法，换言之就是，只要我能到达左边那个位置或者上面那个位置，那么我一定能够到达当前所求的这个位置，那么也就说明，到达上面/左边位置的路径均能到达我当前的位置，那么两个地方的路径数之和就是到达当前位置的路径数之和~ 这里就不贴图了 ，如果文字描述不清楚，可以结合上面的xyz那张图（也就是所有图中的第三张图）进行结合理解。
动态规划变种很多，前些时候做了些公司面试笔试题 ，发现很多题可以用动态规划来做，但是不得其解，文中的题目是比较清晰的，容易推出动态规划递推式的类型，对于一些变种，还需要多做多总结！欢迎各位读者在评论区进行讨论，有更好的方法我也很愿意与您交流学习！
如果文章对您有帮助，可以点个小赞哦~