7020.统计对称整数的数目

思路一：指定区间统计对称整数

• 1.遍历区间
• 2.判断该数对不对称
  • 对称逻辑：首尾同时开始遍历，并且同时累加为两个数，最后判断两个数是否相等

class Solution {
public:
    bool judge(int num){
        if(num<=10) return false;//特例1
        string str=to_string(num);
        if(str.size()%2!=0) return false;//特例2
        int left=0,right=str.size()-1,suml=0,sumr=0;
        while(left<right){//首尾同时累加
            suml+=str[left++]-'0';
            sumr+=str[right--]-'0';
        }
        if(suml!=sumr) return false;//判断累加的数是否相等
        
        return true;
    }
    int countSymmetricIntegers(int low, int high) {
        int res=0;
        for(int i=low;i<=high;i++){
            if(judge(i)) res++;
        }
        return res;
    }
};

8040.生成特殊字符的最少操作

分析：刚开始想到回溯，但是实际做起来发现不太好找，甚至有些多余

思路一：直接两个for循环遍历，找到两个数可以被25整除，并且更新这两个数位于整个字符串的较右侧

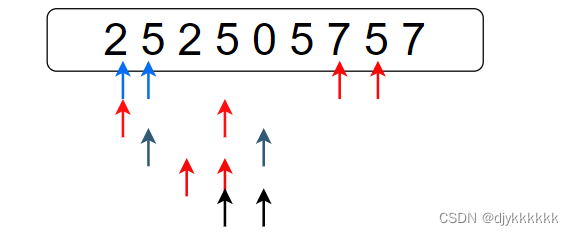
如图：较右侧显然为75，所以在编写时，需要更新 i 为最大 （部分没标出）

class Solution {
public:

    int minimumOperations(string num) {
        if(num.size()<7){
            if(stoi(num)%25==0) return 0;//主要判断有的可以直接被25整除
            // else return num.size();
        }
        int left=INT_MIN,right=0,count=0;
        string mid;
        for(int i=0;i<num.size()-1;i++){
            if(num[i]=='0') count++;//记录0的个数
            for(int j=i+1;j<num.size();j++){
                if(num[j]=='0') count++;//有i遍历不到的j记录
                mid.push_back(num[i]);
                mid.push_back(num[j]);
                
                if(mid=="25" || mid=="00" || mid=="75" || mid=="50"){//在找到符合的情况下
                    if(i>left){//找到i最大
                        left=i;
                        right=j;
                        cout<<left<<endl;
                    }
                }
                mid.clear();
            }
        }
        if(left==INT_MIN){//如果前面没找到有可以整除25的组合
            //cout<<123;
            if(count>0) return num.size()-1;//存在0的话，可以最后剩一个0（00已经找过）
            return num.size();
        }
        return num.size()-left-2;//整个数组长度-整除的数开始位置=整除的数+多余的数
                                 //整除的数为两位：所以此时-2就只剩多余的数
    }
};