本篇博客介绍:介绍二叉树的相关算法
二叉树相关算法
- 二叉树结构
- 遍历二叉树
- 递归序
- 二叉树的交集
- 非递归方式实现二叉树遍历
- 二叉树的层序遍历
- 二叉树难题
- 二叉树的序列化和反序列化
- lc431
- 求二叉树最宽的层
- 二叉树的后继节点
- 谷歌面试题
二叉树结构
如果对于二叉树的结构还有不了解的同学可以参考我的这篇博客
初识二叉树
遍历二叉树
在学习二叉树算法的时候最经典的题目就是递归遍历二叉树
leetcode题目连接和解法如下
遍历二叉树
我们最常使用的就是递归方法了 先序的整体思想就是先打印头节点 再打印左子树 再打印右子树
class Solution {
public:
void _preorderTraversal(TreeNode* root , vector<int>& v)
{
if (root == nullptr)
{
return;
}
v.push_back(root->val);
_preorderTraversal(root->left, v);
_preorderTraversal(root->right, v);
}
vector<int> preorderTraversal(TreeNode* root)
{
vector<int> v;
_preorderTraversal(root , v);
return v;
}
};
核心代码就是这三行
递归序
v.push_back(root->val);
_preorderTraversal(root->left, v);
_preorderTraversal(root->right, v);
可是大家有没有想过 为什么我们能通过递归方法得到这个结果呢?
为什么它们的名字叫做先序后序中序呢?
因为这本质上其实是递归序加工的结果
假设我们现在有如下一颗二叉树
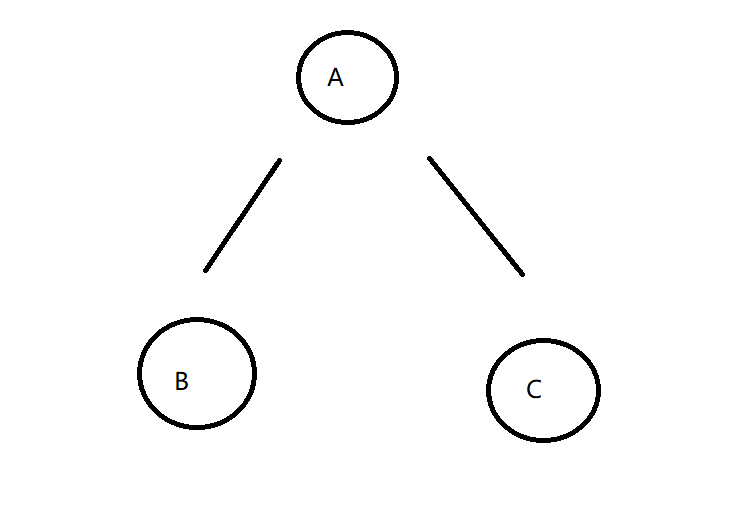
按照我们先序遍历的代码 访问节点的顺序如下
A B B B A C C C A
这个时候我们就可以发现
- 如果我们按照第一次出现的顺序打印就是先序遍历
- 如果我们按照第二次出现的顺序打印就是中序遍历
- 如果我们按照第三次出现的顺序打印就是后序遍历
所以说 先序 中序 后序本质上就是对于递归序的再加工
注:因为我们这里算上主函数调用了三次 所以说会有三次遍历到该节点 如果说调用了四次的话就会访问四次了
二叉树的交集
假设二叉树的先序遍历顺序为 A X B
二叉树的后序遍历顺序为 C X D
其中 A B C D为集合 X是任意一个节点
试证明 A集合交上D集合的子集一定为X的祖先节点
我们要通过两步来证明上面结论的正确性
- 祖先节点在A D集合的子集中
- 其他的节点不在A D集合的子集中
祖先节点在A D集合的子集中
我们都知道 先序遍历的顺序是 头 左 右
后序遍历的顺序是 左 右 头
所以说在先序遍历中 不管X为左子树还是右子树上的节点 它的祖先节点一定是在前面
在后序遍历中 不管X为左子树还是右子树上的节点 它的祖先节点一定是在后面
证毕
其他的节点不在A D集合的子集中
其他节点有四种情况
- 当X作为一个左子树时
- 当X作为一个右子树时
- 当X作为一个左子树上节点时它的右兄弟们
- 当X作为一个右子树上节点时它的左兄弟们
因为这四个问题实际上是两个镜像问题 所以我们讨论两个即可证明完毕
当X作为一个左子树(头节点)时
因为先序遍历的顺序为 头 左 右 所以说它的左右节点肯定在后面的集合中
因为后序遍历的顺序为 左 右 头 所以说它的左右节点肯定在前面的集合中
所以当X作为一个左子树时 它的子节点们不可能有交集
当X为右子树的时候同理
当X作为左子树上的一个节点的时
因为先序遍历的顺序为 头 左 右 所以说它的右兄弟们肯定是在后面的集合中
后序遍历的顺序为 左 右 头 所以说它的右兄弟们们肯定也是在后面的集合中
显然不属于A D的交集
当X作为一个右子树的时候同理
证明完毕
非递归方式实现二叉树遍历
面试中一般不会让我们使用递归方式来实现二叉树的遍历 如果我们用了 面试官也会让我们重新再使用非递归的方式写一遍
所以说我们也要掌握非递归方式的二叉树遍历
非递归方式实现二叉树的前序遍历
前序遍历的顺序是 头 左 右
我们可以通过栈结构来实现该遍历顺序
- 首先将头节点压栈
- 头节点出栈 之后将头节点的左右子节点按照右 左的顺序分别压栈(如果不存在就不操作)
- 接着弹出栈顶的一个元素 当作一个新的头节点来操作
- 重复步骤2 3 直到栈为空
这个的原理就是 我们可以将每个节点都看作是一个头节点 它的遍历顺序一定是 头 左 右
那么我们按照栈的顺序去运行(先入栈右 再入栈左) 那么遍历的顺序肯定是 头节点 左节点 右节点 而遍历到下一个节点的时候 又会是重复一遍上面的操作(相当于分解成了一个个的小任务)
所以说会造成先序遍历的效果
代码表示如下
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> v;
if (root == nullptr)
{
return v;
}
st.push(root);
TreeNode* cur = nullptr;
while(!st.empty())
{
cur = st.top();
st.pop();
if (cur->right)
{
st.push(cur->right);
}
if (cur->left)
{
st.push(cur->left);
}
v.push_back(cur->val);
}
return v;
}
};
非递归方式实现二叉树的后序遍历
我们前序遍历既然能通过压栈顺序实现头 左 右的顺序
那么我们控制下左右节点进入的时间我们就可以实现 头 右 左的顺序
之后我们再逆序一下 就能完成 左 右 头的顺序了 这也就是后序遍历的顺序
代码表示如下
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> v;
if (root == nullptr)
{
return v;
}
st.push(root);
TreeNode* cur = nullptr;
while(!st.empty())
{
cur = st.top();
st.pop();
if (cur->left)
{
st.push(cur->left);
}
if (cur->right)
{
st.push(cur->right);
}
v.push_back(cur->val);
}
reverse(v.begin() , v.end());
return v;
}
};
非递归方式实现二叉树的中序遍历
其实中序遍历改非递归是最难理解的 但是实际上代码量并不多
- 头节点先进栈
- 我们设置一个当前指针cur指向栈中的第一个节点 以这个节点作为头节点 它的左节点全部入栈 直到遇到空节点为止
- 遇到空节点之后取出栈中的头节点 并且将其右节点入栈 (如果存在的话)
- 重复步骤2 3
代码表示如下
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root)
{
vector<int> v;
if (root == nullptr)
{
return v;
}
stack<TreeNode*> st;
TreeNode* cur = root;
while (!st.empty() || cur != nullptr)
{
if (cur)
{
st.push(cur);
cur = cur->left;
}
else
{
cur = st.top();
st.pop();
v.push_back(cur->val);
cur = cur->right;
}
}
return v;
}
};
原理解释如下
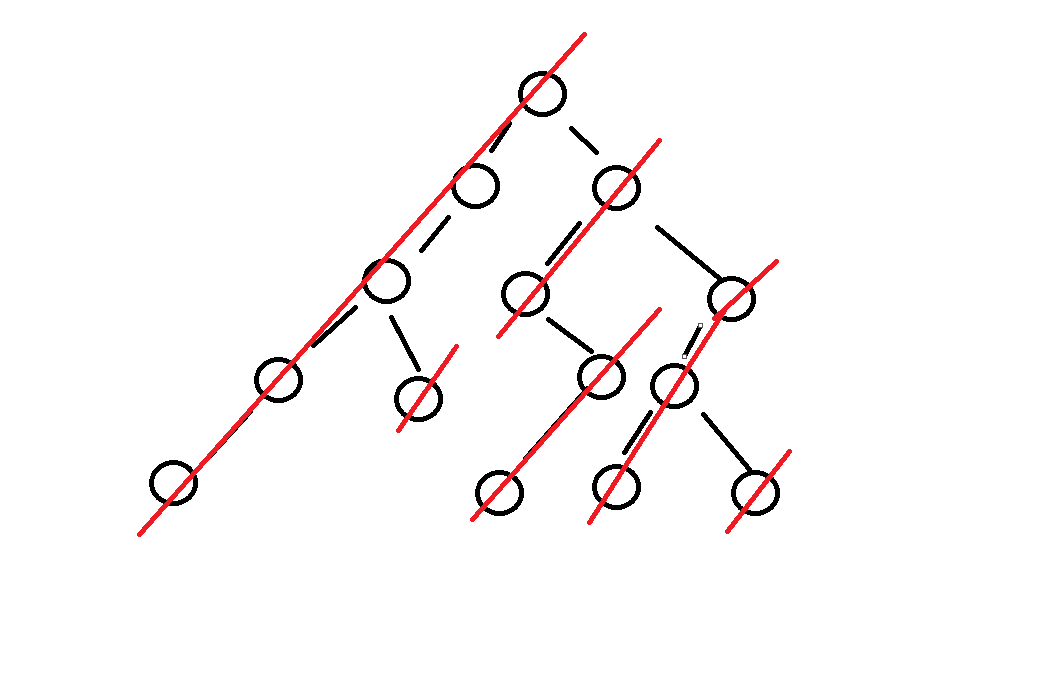
如上图所示 我们的二叉树一定可以被一颗子树的左边界分隔为两部分的
而对于整棵树来说 我们是先把我们的左边界压到栈中去的 所以说我们遍历的顺序一定是先左的
而当我们遍历到空的时候 我们会先打印当前节点 也就是 头
之后节点跳向右(也就是遍历右节点了)
而由于我们是按照栈的顺序存储着这些节点的 所以说一定是处理完左边界的每一棵树才会处理上面的内容 于是乎便会达到我们中序遍历的目的了
二叉树的层序遍历
关于层序遍历问题 博主之前写过博客介绍 这里就不过过多赘述了 具体可以参考我的这篇博客
二叉树的层序遍历
二叉树难题
二叉树的序列化和反序列化
二叉树的序列化和反序列化是leetcode上一道十分著名的题目
可是抛开这个题目本身不谈 二叉树的序列化和反序列化本身也是我们日常工作一个很重要的内容
这里首先介绍下序列化和反序列化
- 序列化: 将对象转化为字节流的过程
- 反序列化: 将字节流转化为对象的过程
因为我们平时在工作中 二叉树是保存在内存中的 而在内存中的二叉树结构我们并不能持久化保存 所以说我们需要进行序列化 方便在任何时间任何地点复现这颗二叉树
而序列化的一种比较好的方式 就是将二叉树转化为字符串
序列化一共有两种方式
一种是前序遍历序列化 一种是层序遍历序列化
前序遍历序列化和反序列化
前序遍历序列化要说简单其实也很简单
我们只需要按照前序的顺序将二叉树构造成一个字符串就行 如果出现空节点我们就将空节点定义为一个特殊字符比如说 ',' 又比如说 '*'
下面是序列化的代码
void rserialize(TreeNode* root , string& str)
{
if (root == nullptr)
{
str += "None,";
}
else
{
str += to_string(root->val) + ",";
rserialize(root->left , str);
rserialize(root->right , str);
}
}
string serialize(TreeNode* root)
{
string ret;
rserialize(root, ret);
return ret;
}
TreeNode* rdeserialize(list<string>& dataArray)
{
if (dataArray.front() == "None")
{
dataArray.erase(dataArray.begin());
return nullptr;
}
TreeNode* root = new TreeNode(stoi(dataArray.front()));
dataArray.erase(dataArray.begin());
root->left = rdeserialize(dataArray);
root->right = rdeserialize(dataArray);
return root;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data)
{
list<string> dataArray;
string str;
for (auto& ch : data)
{
if (ch == ',')
{
dataArray.push_back(str);
str.clear();
}
else
{
str.push_back(ch);
}
}
if (!str.empty())
{
dataArray.push_back(str);
str.clear();
}
return rdeserialize(dataArray);
}
层序遍历序列化
层序遍历的序列化方式和层序遍历其实大差不差 唯一的区别就是将空指针也放入到其中(比如说我下面就使用None来标识一个空指针)
string serialize(TreeNode* root)
{
if (root == nullptr)
{
return "";
}
list<string> dataArray;
TreeNode* cur = root;
dataArray.push_back(to_string(cur->val) + ",");
queue<TreeNode*> q;
q.push(root);
while (!q.empty())
{
cur = q.front();
q.pop();
if (cur -> left)
{
dataArray.push_back(to_string(cur->left->val) + ",");
q.push(cur->left);
}
else
{
dataArray.push_back("None,");
}
if (cur->right)
{
dataArray.push_back(to_string(cur->right->val) + ",");
q.push(cur->right);
}
else
{
dataArray.push_back("None,");
}
}
string ans;
for (auto x : dataArray)
{
ans += x;
}
return ans;
}
层序遍历的反序列化
反序列化的时候我们可以先将字符串分隔并且放到一个list中
再初始化一个队列 我们一次实例化每个队列中节点的左右子节点 如果非空则我们将左右节点放入到队列中去
// Decodes your encoded data to tree.
TreeNode* deserialize(string data)
{
if (data == "")
{
return nullptr;
}
list<string> dataArray;
string str;
for (auto ch : data)
{
if (ch == ',')
{
dataArray.push_back(str);
str.clear();
}
else
{
str += ch;
}
}
TreeNode* cur = Build(dataArray.front());
dataArray.erase(dataArray.begin());
TreeNode* root = cur;
queue<TreeNode*> que;
que.push(cur);
while (!que.empty() || !dataArray.empty())
{
cur = que.front();
que.pop();
cur -> left = Build(dataArray.front());
dataArray.erase(dataArray.begin());
cur -> right = Build(dataArray.front());
dataArray.erase(dataArray.begin());
if (cur -> left)
{
que.push(cur->left);
}
if (cur->right)
{
que.push(cur->right);
}
}
return root;
}
lc431
求二叉树最宽的层
该题目使用层序遍历就能很简单的解决 这里就不过多讲解了
二叉树的层序遍历参考上面的代码
二叉树的后继节点
首先我们给出定义 二叉树的后继节点就是在二叉树的中序遍历顺序中 该节点的下一个节点 (如果存在的话)
比如说下面这一棵二叉树
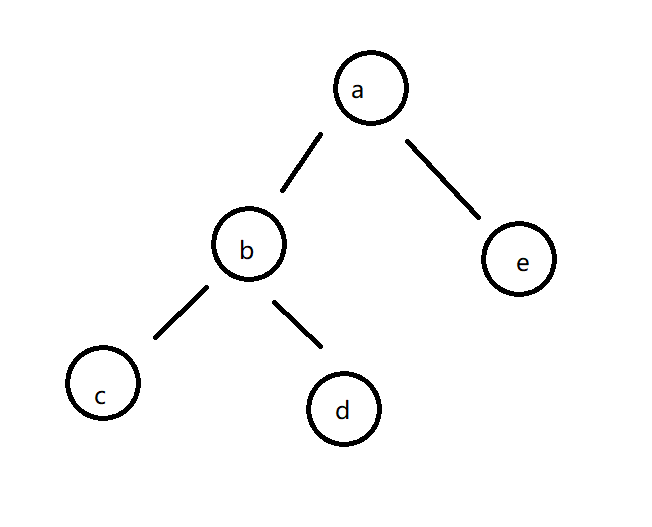
d的后继节点就是a
解决这个问题主要分两种情况讨论
- d节点有右孩子
- d节点没有右孩子
d节点有右孩子
如果d节点有右孩子的话 我们只需要找到它右子树的最左节点即可
(因为d节点打印完之后肯定打印它的右子树 而它右子树的最左节点则是最先被打印的)
d节点没有右孩子
此时我们向上找它的父节点
- 如果它是父节点的左孩子 那么父节点就是它的后继节点(因为这个时候父节点的左子树全部中序遍历完了)
- 如果它是父节点的右孩子 则一直向上找父节点 直到找到为止
谷歌面试题
我们拿出一个长纸条
先对折一次 我们会发现纸条中间出现了一个凹折痕 我们将其标记为1凹

之后我们将其恢复成对折一次的样子 再次对折 之后我们会发现 多出了两条新的折痕我们将凹下去的折痕标记为2凹 凸起的折痕标记为2凸
之后再重复上面的步骤一次 我们就能够得到下面这张图

通过观察我们可以发现 每个小折痕在对折之后就会在它的上下两侧出现一凹一凸两个折痕
由此我们就可以联想到二叉树
实际上就是 从头节点开始 头节点是凹折痕 之后它的左节点的凹折痕 右节点是凸折痕
以此类推
如果我们要通过中序遍历的方式从上到下打印出这些折痕 我们可以写出以下代码
我们定义 当bool b为真时是凹折痕 当为假时为凸折痕
那么代码如下
void process(int i , int n , bool b)
{
if (i > n)
{
return;
}
process(i+1 , n , 1);
if (b)
{
cout << "a " ;
}
else
{
cout << "b ";
}
process(i+1 , n , 0);
}
上面折断代码的意思是 我们假设这颗二叉树有n层高 我们目前在第i层
如果i>n 说明条件不满足 结束
之后我们让左节点打印a 右节点打印b 自己如果bool类型为真打印a 否则b

我们可以看到 与我们画的图一致