【C++ 二叉搜索树】

news2024/11/24 9:33:59

目录

  • 1.什么是二叉搜索树
  • 2.构建二叉搜索树
    • 2.1首先搭建树的框架
    • 2.2搭建搜索树的框架
  • 3.二叉搜索树的插入
    • 3.1非递归式插入
    • 3.2递归式插入
  • 4.二叉搜索树的查找
    • 4.1非递归查找
    • 4.2递归查找
  • 5.二叉搜索树的删除
    • 5.1非递归删除
    • 5.2递归删除
  • 6.整个代码实现

1.什么是二叉搜索树

简单来讲就是一个树的左子树的值都小于根，右子树的值都大于根。如：
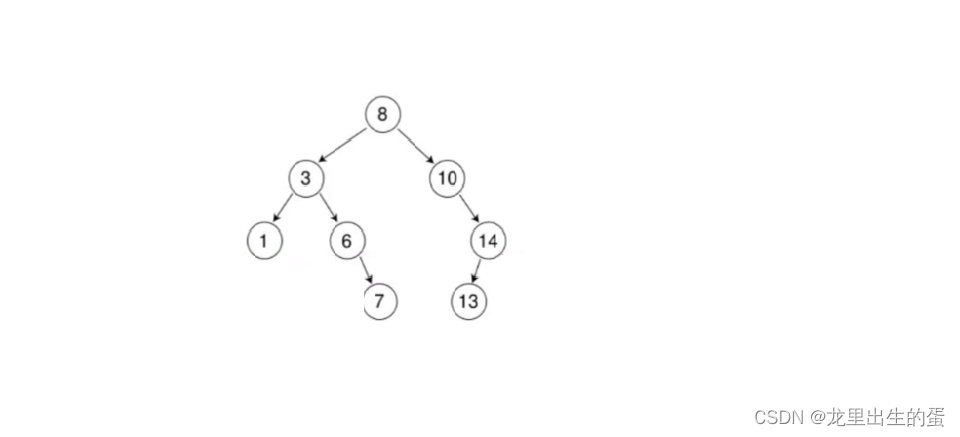
在这里插入图片描述
这个树的特点是走一趟中序就完成了对一组树的排序。查找一个树也特别的方便，最多只需要走树的高度次。所以当这个树比较饱满时搜索的效率很高，所以被称为二叉搜索树。

2.构建二叉搜索树

2.1首先搭建树的框架

struct TreeNode
{
	TreeNode<V>* _left;
	TreeNode<V>* _right;
	V _val;

	//构造函数
	TreeNode(V val)
	{
		_left = nullptr;
		_right = nullptr;
		_val = val;
	}
};

2.2搭建搜索树的框架

template<class V>
class BSTree
{
	typedef TreeNode<V> Node;
public:
	BSTree()
	{
		_head = nullptr;
	}
	private:
	Node* _head;
	
};

3.二叉搜索树的插入

3.1非递归式插入

1.思路
在这里插入图片描述
2.代码

//插入(非递归)
	bool insert(V val)
	{
		if (_head == nullptr)
		{
			_head = new Node(val);
			return true;
		}
		//找到要插入结点的位置
		Node* parent = _head;
		Node* cur = _head;
		while (cur)
		{
			if (cur->_val < val)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_val > val)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//相等  返回false
				return false;
			}
		}
		//判断val插在parent的左还是右
		if (parent->_val >val)
		{
			parent->_left = new Node(val);
			return true;
		}
		else
		{
			parent->_right = new Node(val);
			return true;
		}

3.2递归式插入

	bool insertR(V val)
	{
		return _insertR(_head, val);
	}
	
    bool _insertR(Node*& head, V val)
	{
		if (head == nullptr)
		{
			head = new Node(val);
			return true;
		}
		if (head->_val > val)
		{
			_insertR(head->_left,val);
		}
		else if (head->_val < val)
		{
			_insertR(head->_right, val);
		}
		else
		{
			return false;
		}
		return false;
		
	}

注意点：这个递归式插入其实也没什么难的，就是有个注意点是要引用传参。如果不是引用传参是不会修改-head的。

4.二叉搜索树的查找

4.1非递归查找

//非递归查找
bool find(V val)
{
	if (_head == nullptr)
	{
		return false;
	}
	Node* cur = _head;
	while (cur)
	{
		if (cur->_val < val)
		{
			cur = cur->_right;
		}
		else if (cur->_val > val)
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
}

4.2递归查找

bool findR(const V& val)
{
	return _findR(_head, val);
}

bool _findR(Node* head, const V& val)
{
	if (head == nullptr)
	{
		return false;
	}
	if (head->_val == val)
	{
		return true;
	}
	return _findR(head->_left, val) || _findR(head->_right, val);
}

比较常规，没什么要解释的。

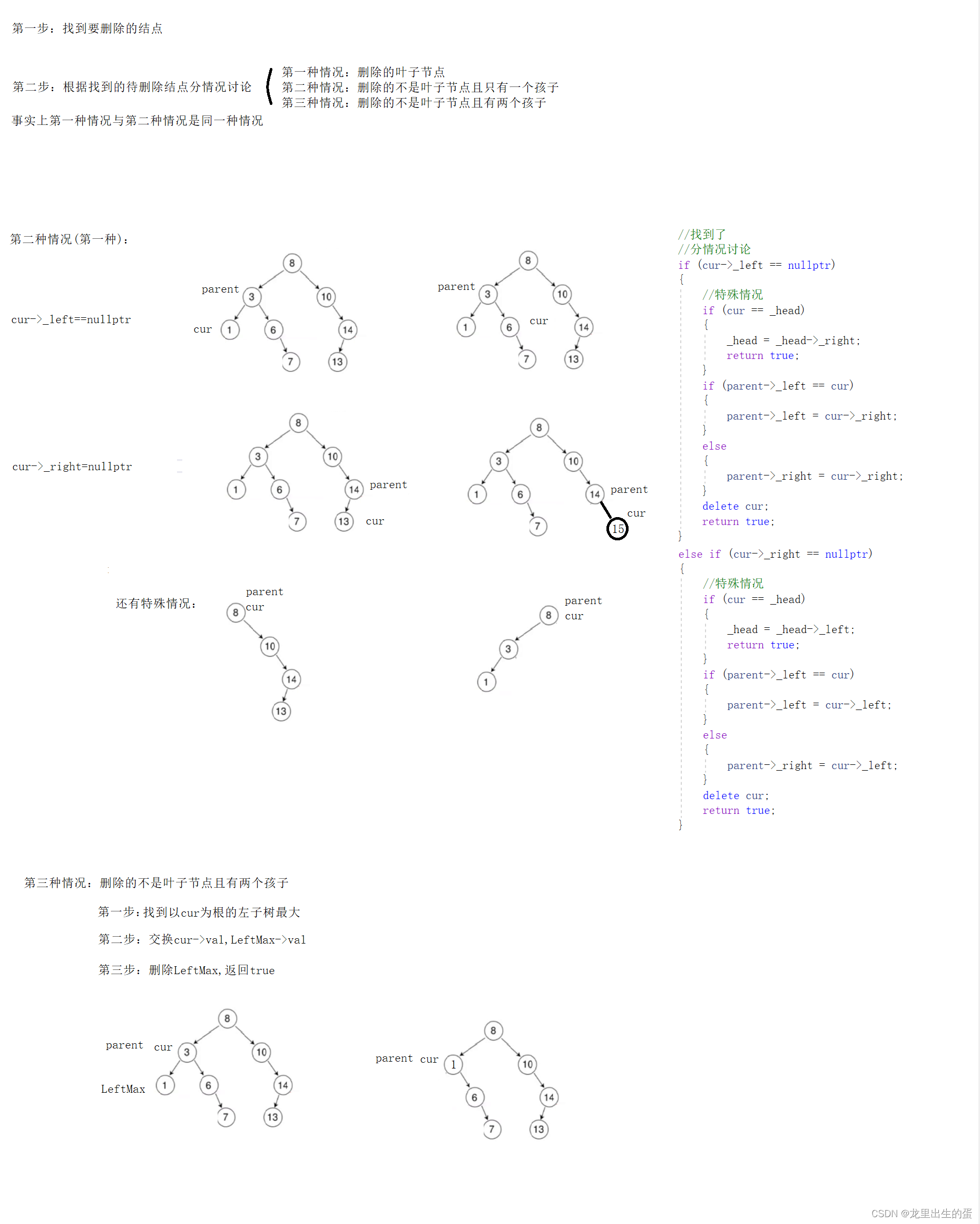
5.二叉搜索树的删除

5.1非递归删除

算法思路：
在这里插入图片描述

代码实现：

//非递归式删除
bool erase(const V& val)
{
	//第一步找到要删除的结点
	Node* parent = _head;
	Node* cur = _head;
	while (cur)
	{
		if (cur->_val > val)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_val < val)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			//找到了
			//分情况讨论
			if (cur->_left == nullptr)
			{
				//特殊情况
				if (cur == _head)
				{
					_head = _head->_right;
					return true;
				}
				if (parent->_left == cur)
				{
					parent->_left = cur->_right;
				}
				else
				{
					parent->_right = cur->_right;
				}
				delete cur;
				return true;
			}
			else if (cur->_right == nullptr)
			{
				//特殊情况
				if (cur == _head)
				{
					_head = _head->_left;
					return true;
				}
				if (parent->_left == cur)
				{
					parent->_left = cur->_left;
				}
				else
				{
					parent->_right = cur->_left;
				}
				delete cur;
				return true;
			}
			else
			{
				//找LeftMax
				Node* parent = cur;
				Node* LeftMax = cur->_left;
				while (LeftMax->_right)
				{
					parent = LeftMax;
					LeftMax = LeftMax->_right;
				}

				//交换cur与LeftMax的val
				swap(cur->_val, LeftMax->_val);

				if (parent->_left == LeftMax)
				{
					parent->_left = LeftMax->_right;
				}
				else
				{
					parent->_right = LeftMax->_right;
				}
				delete LeftMax;
				return true;
			}
		}
	}
	return false;
}

注：这个非递归主要就是要完全考虑到删除结点会出现的可能，代码实现不复杂，但是很难一起写对，写错了调试也好很久(本人亲身经历调试了一个下午)。

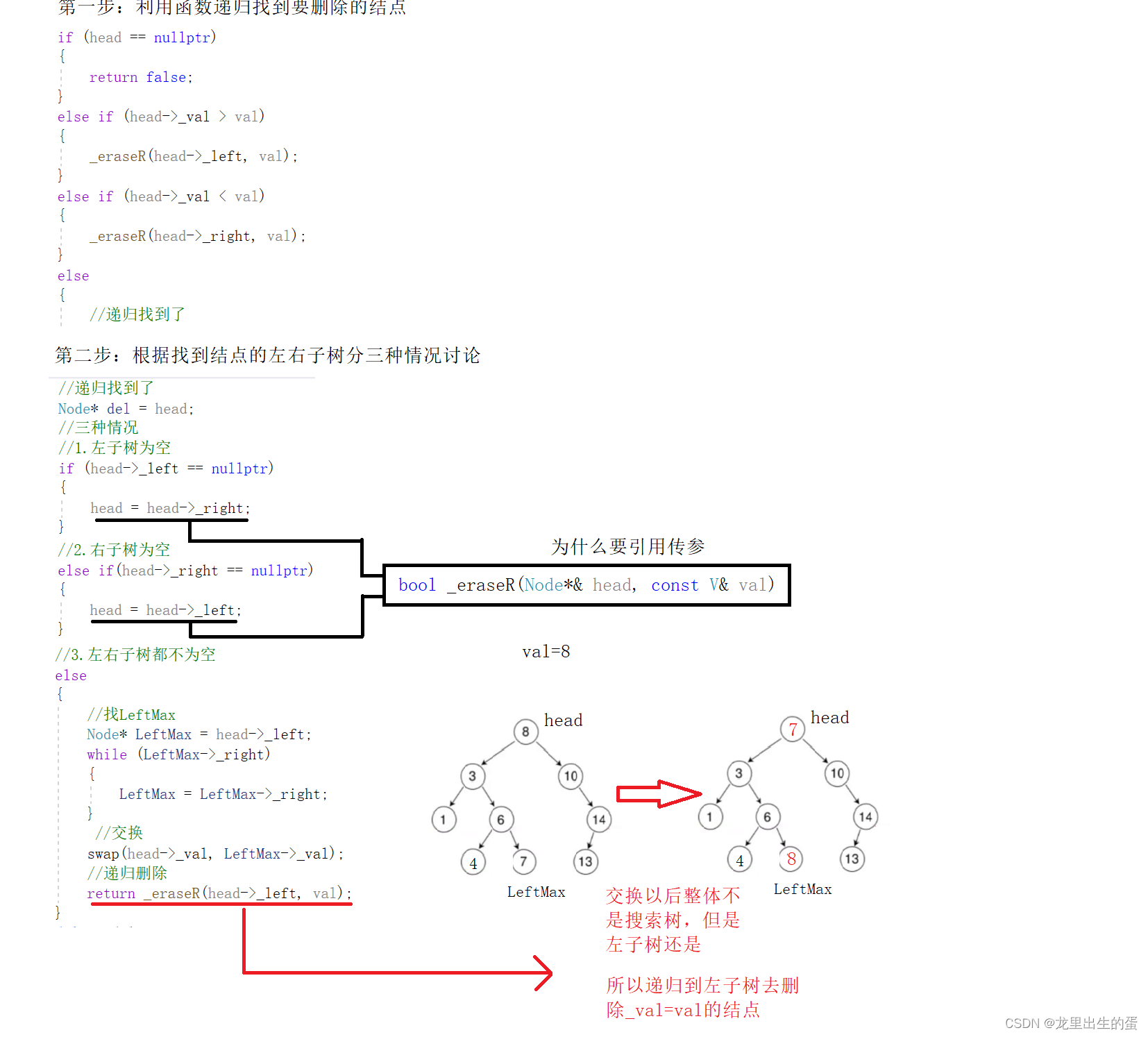
5.2递归删除

算法思路：
在这里插入图片描述

代码实现：

bool _eraseR(Node*& head, const V& val)
	{
		if (head == nullptr)
		{
			return false;
		}
		else if (head->_val > val)
		{
			_eraseR(head->_left, val);
		}
		else if (head->_val < val)
		{
			_eraseR(head->_right, val);
		}
		else
		{
			//递归找到了
			Node* del = head;
			//三种情况
			//1.左子树为空
			if (head->_left == nullptr)
			{
				head = head->_right;
			}
			//2.右子树为空
			else if(head->_right == nullptr)
			{
				head = head->_left;
			}
			//3.左右子树都不为空
			else
			{
				//找LeftMax
				Node* LeftMax = head->_left;
				while (LeftMax->_right)
				{
					LeftMax = LeftMax->_right;
				}
				 //交换
				swap(head->_val, LeftMax->_val);
				//递归删除
				return _eraseR(head->_left, val);
			}
			delete del;
			return true;
		}
	}

6.整个代码实现

#pragma once
template<class V>
struct TreeNode
{
	TreeNode<V>* _left;
	TreeNode<V>* _right;
	V _val;

	//构造函数
	TreeNode(V val)
	{
		_left = nullptr;
		_right = nullptr;
		_val = val;
	}
};

template<class V>
class BSTree
{
	typedef TreeNode<V> Node;
public:
	BSTree()
	{
		_head = nullptr;
	}

	//深拷贝
	BSTree(BSTree<V>& bs)
	{
		_head = CopyTree(bs._head);
	}

	//赋值
	BSTree<V>& operator=(BSTree<V> bs)
	{
		swap(_head, bs._head);
		return *this;
	}
	
	//插入(非递归)
	bool insert(V val)
	{
		if (_head == nullptr)
		{
			_head = new Node(val);
			return true;
		}
		//找到要插入结点的位置
		Node* parent = _head;
		Node* cur = _head;
		while (cur)
		{
			if (cur->_val < val)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_val > val)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//相等  返回false
				return false;
			}
		}
		//判断val插在parent的左还是右
		if (parent->_val >val)
		{
			parent->_left = new Node(val);
			return true;
		}
		else
		{
			parent->_right = new Node(val);
			return true;
		}
	}

	bool insertR(V val)
	{
		return _insertR(_head, val);
	}

	//非递归查找
	bool find(V val)
	{
		if (_head == nullptr)
		{
			return false;
		}
		Node* cur = _head;
		while (cur)
		{
			if (cur->_val < val)
			{
				cur = cur->_right;
			}
			else if (cur->_val > val)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
	}

	bool findR(const V& val)
	{
		return _findR(_head, val);
	}



	~BSTree()
	{
		destory(_head);
	}

	void inorder()
	{
		_inorder(_head);
		cout << endl;
	}

	//非递归式删除
	bool erase(const V& val)
	{
		//第一步找到要删除的结点
		Node* parent = _head;
		Node* cur = _head;
		while (cur)
		{
			if (cur->_val > val)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_val < val)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//找到了
				//分情况讨论
				if (cur->_left == nullptr)
				{
					//特殊情况
					if (cur == _head)
					{
						_head = _head->_right;
						return true;
					}
					if (parent->_left == cur)
					{
						parent->_left = cur->_right;
					}
					else
					{
						parent->_right = cur->_right;
					}
					delete cur;
					return true;
				}
				else if (cur->_right == nullptr)
				{
					//特殊情况
					if (cur == _head)
					{
						_head = _head->_left;
						return true;
					}
					if (parent->_left == cur)
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;
					}
					delete cur;
					return true;
				}
				else
				{
					//找LeftMax
					Node* parent = cur;
					Node* LeftMax = cur->_left;
					while (LeftMax->_right)
					{
						parent = LeftMax;
						LeftMax = LeftMax->_right;
					}

					//交换cur与LeftMax的val
					swap(cur->_val, LeftMax->_val);

					if (parent->_left == LeftMax)
					{
						parent->_left = LeftMax->_right;
					}
					else
					{
						parent->_right = LeftMax->_right;
					}
					delete LeftMax;
					return true;
				}
			}
		}
		return false;
	}


	bool eraseR(const V& val)
	{
		return _eraseR(_head, val);
	}




private:
	Node* _head;

	void destory(Node*& head)
	{
		if (head == nullptr)
		{
			return;
		}
		destory(head->_left);
		destory(head->_right);

		delete head;
		head = nullptr;
	}

	bool _insertR(Node*& head, V val)
	{
		if (head == nullptr)
		{
			head = new Node(val);
			return true;
		}
		if (head->_val > val)
		{
			_insertR(head->_left,val);
		}
		else if (head->_val < val)
		{
			_insertR(head->_right, val);
		}
		else
		{
			return false;
		}
		return false;
		
	}

	void _inorder(Node* head)
	{
		if (head == nullptr)
		{
			return;
		}
		_inorder(head->_left);
		cout << head->_val << " ";
		_inorder(head->_right);
	}

	bool _findR(Node* head, const V& val)
	{
		if (head == nullptr)
		{
			return false;
		}
		if (head->_val == val)
		{
			return true;
		}
		return _findR(head->_left, val) || _findR(head->_right, val);
	}

	bool _eraseR(Node*& head, const V& val)
	{
		if (head == nullptr)
		{
			return false;
		}
		else if (head->_val > val)
		{
			_eraseR(head->_left, val);
		}
		else if (head->_val < val)
		{
			_eraseR(head->_right, val);
		}
		else
		{
			//递归找到了
			Node* del = head;
			//三种情况
			//1.左子树为空
			if (head->_left == nullptr)
			{
				head = head->_right;
			}
			//2.右子树为空
			else if(head->_right == nullptr)
			{
				head = head->_left;
			}
			//3.左右子树都不为空
			else
			{
				//找LeftMax
				Node* LeftMax = head->_left;
				while (LeftMax->_right)
				{
					LeftMax = LeftMax->_right;
				}
				 //交换
				swap(head->_val, LeftMax->_val);
				//递归删除
				return _eraseR(head->_left, val);
			}
			delete del;
			return true;
		}
	}

	Node* CopyTree(Node* head)
	{
		if (head == nullptr)
		{
			return nullptr;
		}
		Node* newhead = new Node(head->_val);
		newhead->_left = CopyTree(head->_left);
		newhead->_right = CopyTree(head->_right);

		return newhead;
	}
	
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/970604.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

WebDAV之π-Disk派盘 + 小书匠

WebDAV之π-Disk派盘 + 小书匠

小书匠是一款功能丰富，强大的知识管理工具。全平台覆盖，离线数据存储，自定义数据服务器，所见即所得的 markdown 编辑体验。 小书匠提供了多种实用的编辑模式，例如：栏编辑、双栏编辑、三栏编辑、全屏写作、全屏阅读等。并且该软件还提供了许多有用的扩展语法，比如Latex公…
阅读更多...
【前端demo】CSVJSON转换器 原生实现：CSV转换为JSON，JSON转换为CSV

【前端demo】CSVJSON转换器 原生实现：CSV转换为JSON，JSON转换为CSV

文章目录 效果过程textareaTooltip提示工具按钮的min-width判断输入是否是CSV或JSONJSON与CSV样例JSON转为CSVCSV转为JSON不足之处 代码HTMLCSSJS 其他demo 效果 效果预览&#xff1a;CSV&JSON Converter (codepen.io) 参照的预览&#xff1a;JSV Converter(gpaiva00.git…
阅读更多...
地毯16 CFR 1630/1631安全防火性易燃性测试

地毯16 CFR 1630/1631安全防火性易燃性测试

地毯的16 CFR 1630/1631安全防火性易燃性测试是一项重要的产品检测认证标准。该测试旨在评估地毯材料的防火性能&#xff0c;以确保其在使用过程中不会引发火灾或加剧火势。测试过程包括对地毯样品进行燃烧测试和燃烧后的评估。 根据16 CFR 1630标准&#xff0c;地毯样品将被暴…
阅读更多...
检漏仪和高真空度控制技术在热管漏率和内部真空度测量中的应用

检漏仪和高真空度控制技术在热管漏率和内部真空度测量中的应用

摘要&#xff1a;大量MEMS真空密封件具有小体积、高真空和无外接通气接口的特点&#xff0c;现有的各种检漏技术无法对其进行无损形式的漏率和内部真空度测量。基于压差法和高真空度恒定控制技术&#xff0c;本文提出了解决方案。方案的具体内容是将被测封装器件放置在一个比器…
阅读更多...
elementui表格自定义表头的两种方法

elementui表格自定义表头的两种方法

表格自定义表头的方式 多选框表头换文字 请查看上篇博客&#xff1a;http://t.csdn.cn/69De2 文字换按钮 render-header render-header方法详情 Table-column Attributes 参数说明类型可选值默认值render-header列标题 Label 区域渲染使用的 FunctionFunction(h, { column, $in…
阅读更多...
恒运资本：北向资金流出一定会跌吗？股票涨跌与什么有关？

恒运资本：北向资金流出一定会跌吗？股票涨跌与什么有关？

北向资金被认为是A股商场的风向标&#xff0c;它的动向往往会影响投资者的心情。那么北向资金流出一定会跌吗&#xff1f;股票涨跌与什么有关&#xff1f;恒运资本也为大家准备了相关内容&#xff0c;以供参阅。 北向资金流出一定会跌吗&#xff1f; 北向资金流出并不一定意味…
阅读更多...
快速解决 adb server version doesn‘t match this client

快速解决 adb server version doesn‘t match this client

这个问题是由于电脑上安装了多个版本的adb工具&#xff0c;客户端和服务端的版本不一致&#xff0c;无法正常通信导致。最快的解决方法就是将Android SDK中adb复制到系统目录下。 操作步骤如下&#xff1a; 1. 查看adb版本和路径 执行adb version&#xff0c;如下&#xff0…
阅读更多...
手机无人直播软件在苹果iOS系统中能使用吗？

手机无人直播软件在苹果iOS系统中能使用吗？

在现代社交媒体的时代&#xff0c;直播带货已经成为了一种热门的销售途径。通过直播&#xff0c;人们可以远程分享自己的商品&#xff0c;与观众进行互动&#xff0c;增强沟通和参与感。而如今&#xff0c;手机无人直播软件更是成为了直播带货领域的一项火爆的技术。那么&#…
阅读更多...
渗透测试——安全漏洞扫描工具APPScan的安装与基本使用步骤

渗透测试——安全漏洞扫描工具APPScan的安装与基本使用步骤

前言 HCL AppScan Standard是安全专家和渗透测试者设计的动态应用程序安全测试工具&#xff0c;AppScan使用强大的扫描引擎&#xff0c;会自动检索目标应用程序并测试漏洞。测试结果按优先级排列&#xff0c;允许操作员快速分类问题、发现最关键的漏洞。每个检测到的问题都可以…
阅读更多...
Python 自学：使用线程模块同时运行代码 Threading

Python 自学：使用线程模块同时运行代码 Threading

1. 以下代码中&#xff0c;程序会等一个函数执行完毕才执行下一个函数。 import timestart time.perf_counter()def do_something():print(Sleeping 1 second...)time.sleep(1)print(Done Sleeping...)do_something() do_something()finish time.perf_counter()print(fFinis…
阅读更多...
惠普NS1005 NS1020打印机如何判断是不是该加粉了

惠普NS1005 NS1020打印机如何判断是不是该加粉了

惠普 Laser NS MFP 1005 1020系列智能闪充加粉式多功能一体机的耗材余量指示灯显示“1” “2” “2”时&#xff0c;就是在“说”&#xff1a;快没有墨粉了&#xff1b; 耗材余量指示灯和充粉口指示灯 在不同的状态下代表不同的意思&#xff0c;当耗材余量指示灯显示“1” “2”…
阅读更多...
2023年9月上海/广州/深圳CSPM-3国标项目管理中级认证招生

2023年9月上海/广州/深圳CSPM-3国标项目管理中级认证招生

CSPM-3中级项目管理专业人员评价&#xff0c;是中国标准化协会&#xff08;全国项目管理标准化技术委员会秘书处&#xff09;&#xff0c;面向社会开展项目管理专业人员能力的等级证书。旨在构建多层次从业人员培养培训体系&#xff0c;建立健全人才职业能力评价和激励机制的要…
阅读更多...
【数据结构-栈】栈基础

【数据结构-栈】栈基础

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…
阅读更多...
java持久化框架JPA，自动执行sql语句的代码实现

java持久化框架JPA，自动执行sql语句的代码实现

在springboot入口处调用&#xff1a; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.boot.CommandLineRunner; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBoot…
阅读更多...
Mac使用VMWare安装centos7回车回退

Mac使用VMWare安装centos7回车回退

Mac使用VMWare安装centos7回车回退 说明&#xff1a;本人电脑是MacBook 14pro M2芯片&#xff0c;安装的为VMWare16.2.5&#xff0c;Centos版本为centos stream9 解决方法&#xff1a;使用VM16.2.5Stream9Debian 11操作系统正常安装 问题&#xff1a;下载了VMWare16和Centos…
阅读更多...
【微服务部署】五、Jenkins+Docker一键打包部署NodeJS（Vue）项目的Docker镜像步骤详解

【微服务部署】五、Jenkins+Docker一键打包部署NodeJS（Vue）项目的Docker镜像步骤详解

NodeJS&#xff08;Vue&#xff09;项目也可以通过打包成Docker镜像的方式进行部署&#xff0c;原理是先将项目打包成静态页面&#xff0c;然后再将静态页面直接copy到Nginx镜像中运行。 一、服务器环境配置 前面说明了服务器Nginx的安装和配置&#xff0c;这里稍微有些不同&a…
阅读更多...
java线程和go协程

java线程和go协程

一、线程的实现 线程的实现方式主要有三种&#xff1a;内核线程实现、用户线程实现、用户线程加轻量级进程混合实现。因为自己只对java的线程比较熟悉一点&#xff0c;所以主要针对java线程和go的协程之间进行一个对比。 线程模型主要有三种&#xff1a;1、内核级别线程&#…
阅读更多...
微服务主流框架概览

微服务主流框架概览

微服务主流框架概览 目录概述需求&#xff1a; 设计思路实现思路分析1.HSF2.Dubbo 3.Spring Cloud5.gRPC Service mesh 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&#xff0c;skip hardness,make a be…
阅读更多...
深入理解作用域、作用域链和闭包

深入理解作用域、作用域链和闭包

​ &#x1f3ac; 岸边的风&#xff1a;个人主页 &#x1f525; 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想&#xff0c;就是为了理想的生活 ! ​ 目录 &#x1f4da; 前言 &#x1f4d8; 1. 词法作用域 &#x1f4d6; 1.2 示例 &#x1f4d6; 1.3 词法作用域的…
阅读更多...
医学专题-多组学在疾病发生发展过程中的研究思路

医学专题-多组学在疾病发生发展过程中的研究思路

研究背景 单一组学数据分析通常用来解释某种特征性的生化指标与某些疾病之间的关联&#xff0c;但无法说明其中复杂的因果关系。从疾病表型或某种生物现象出发&#xff0c;寻找影响疾病发生发展的关键因子或通路&#xff0c;借助高通量的技术手段&#xff0c;设置相应的患者组…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023