给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
————————————————————————————————————
1. 递归法
可以使用前序和后序遍历。前序就是求深度,后续就是求高度。
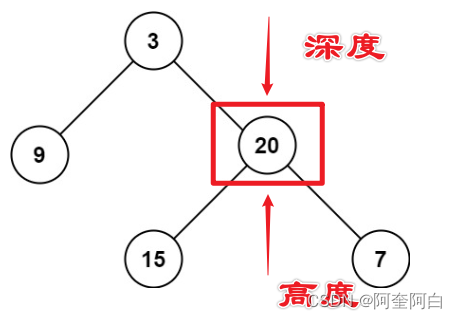
使用后序遍历来计算树的高度。
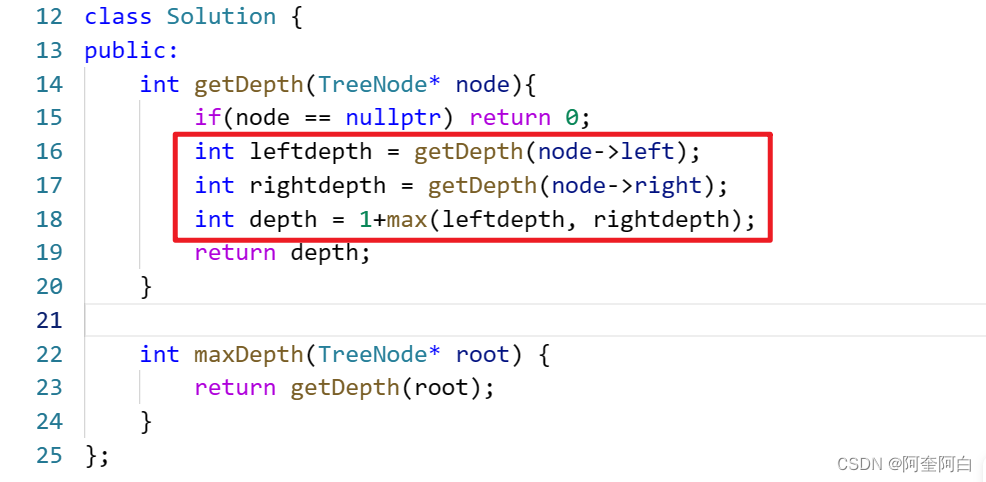 精简之后:
精简之后:
class Solution {
public:
int getDepth(TreeNode* node){
if(node == nullptr) return 0;
return 1+max(getDepth(node->left), getDepth(node->right));
}
int maxDepth(TreeNode* root) {
return getDepth(root);
}
};前序遍历,体现回溯过程:
class Solution {
public:
int result = 0;
void getdepth(TreeNode* node, int depth){
result = depth > result ? depth : result;
if(node->left == nullptr && node->right == nullptr) return;
if(node->left){
depth++; //深度+1
getdepth(node->left, depth);
depth--; //回溯深度-1
}
if(node->right){
depth++;
getdepth(node->right, depth);
depth--;
}
return;
}
int maxDepth(TreeNode* root) {
result = 0;
if(root == nullptr) return result;
getdepth(root, 1);
return result;
}
};2. 迭代法
层序遍历最为合适,遍历的层数就是最大深度。
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr) return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()){
depth++;
int size = que.size();
for(int i=0;i<size;i++){
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return depth;
}
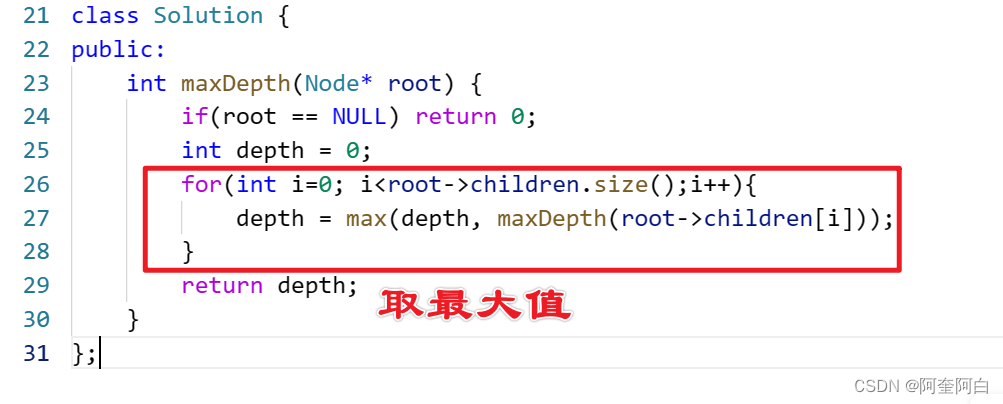
};拓展题:N叉数的最大深度
迭代法:

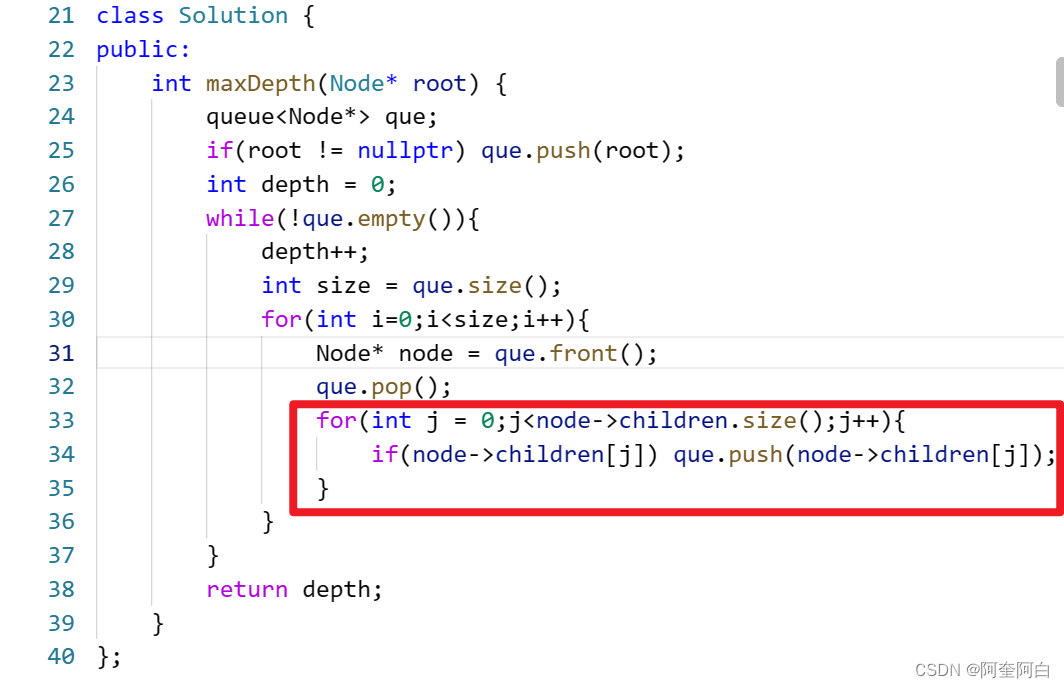
递归法: