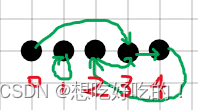
236. Lowest Common Ancestor of a Binary Tree

题意：二叉树，求最近公共祖先，All Node.val are unique.

我的思路

首先把每个节点的深度得到，之后不停向上，直到val相同，存深度就用map存吧

但是它没有向上的指针，要如何解决？——用map<int,int>存一下父节点？

返回的是指针，注意一下

代码 Runtime28 ms Beats 5.86% Memory17.7 MB Beats 5.56%

class Solution {
public:
    unordered_map<int,int>dep; 
    unordered_map<TreeNode*,TreeNode*>fa;
    void dfs(TreeNode* root,int dp){
        if(root==NULL)return;
        dep[root->val]=dp;
        if(root->left)fa[root->left]=root;
        if(root->right)fa[root->right]=root;
        dfs(root->left,dp+1);  dfs(root->right,dp+1);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root,0);
        while(dep[p->val]!=dep[q->val]){
            if(dep[p->val]>dep[q->val]) p=fa[p];
            else q=fa[q];
        }
        while(p!=q){
            p=fa[p];q=fa[q];
        }
        return p;
    }
};

标答递归

情况1：如果p==root||q==root，那就返回root；这里的root是正解

情况2：是指同一层级但不同的指针，而root就是它们的祖先

情况3：p和q都在lca1这里，lca2为NULL不返回

情况4：和情况3类似

代码 Runtime13 ms Beats 73.18% Memory14.2 MB Beats 49.26%

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root)return root;
        if(root->val == p->val || root->val == q->val)return root;//情况1
        TreeNode* lca1=lowestCommonAncestor(root->left,p,q);
        TreeNode* lca2=lowestCommonAncestor(root->right,p,q);
        if(lca1!=NULL&&lca2!=NULL)return root;//情况2
        if(lca1!=NULL)return lca1;//情况3
        return lca2;//情况4
    }
};

标答另一种的不用遍历

用stack来辅助建立每个指针的父指针，这样就不用把整棵树都建完；根据下面的代码来说不能用queue，因为用栈代表的是DFS，而queue就是层序遍历，这样循环终止判断条件mp.find(p)==mp.end() || mp.find(q)==mp.end()就是错误的了

之后用set来每个指针向上，这样就不需要dep了

代码 Runtime24 ms Beats 11.11% Memory17.3 MB Beats 7.82%

class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> s; unordered_map<TreeNode*,TreeNode*> mp;
        mp[root]=NULL; s.push(root);
        while(mp.find(p)==mp.end() || mp.find(q)==mp.end()){
            TreeNode *t=s.top(); s.pop();
            if(t->left){
                mp[t->left]=t; s.push(t->left);
            }
            if(t->right){
                mp[t->right]=t; s.push(t->right);
            }
        }
        set<TreeNode*> sett;
        while(p!=NULL){
            sett.insert(p); p=mp[p];
        }
        while(sett.find(q)==sett.end()){
            q=mp[q];
        }
        return q;
    }
};

238. Product of Array Except Self

题意：给一个数组a，返回一个数组ans，ans[i]等于除了a[i]，其他数的值

我的思路

先判断有多少个0，两个的话都输出0；1个的话，其余的是0，其中一个是除它以外的积；

没有0，那就总积/当前的数

写完了才发现不让用除法

代码 Runtime 11 ms Beats 98.32% Memory24 MB Beats 79.45%

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int zero=0;int mul=1;
        for(int i=0;i<nums.size();i++){
            if(!nums[i])zero++;
            else mul=mul*nums[i];
        }
        vector<int> ans(nums.size(),0);
        if(zero>1)return ans;
        for(int i=0;i<nums.size();i++){
            if(zero&&!nums[i])ans[i]=mul;
            else if(!zero)ans[i]=mul/nums[i];
        }
        return ans;
    }
};

标答前缀积与后缀积

就是普通的做，最后把空间优化了

代码 Runtime14 ms Beats 93.5% Memory24 MB Beats 79.45%

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> output(n);
        output[0] = 1;
        for(int i=1; i<n; i++){
            output[i] = output[i-1] * nums[i-1];
        }
        int right = 1;
        for(int i=n-1; i>=0; i--){
            output[i] *= right;
            right *= nums[i];
        }
        return output;
    }
};

239. Sliding Window Maximum

题意：滑动窗口求最大

我的思路

我记得是用队列做的，因为要求最大值，但是忘了，只记得队列里放的是序号

用单调栈能做吗？不能，例如7 6 5 4 3 2 1

只放比队尾大的数 7 6 5 4 3 2 1 不行

后面想了想，只放比队尾小的数 7 6 5 4 3 2 1好像可以，毕竟是求最大值

标答优先队列 O(nlogn)

初始化pair型的优先队列，答案ans；把k个{数字，序号}放入队列，ans[0]是优先队列的最大的

遍历nums数组，如果优先队列不为空，并且顶部的数字已经小于等于i-k了，那就把顶部的数字不断弹出，之后放入pair，更新答案

代码 Runtime231 ms Beats 48.99% Memory148.9 MB Beats 26.27%

class Solution {
public:
    #define pii pair<int,int> 
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<pii,vector<pii>,less<pii>> q;
        int n=nums.size();
        vector<int> ans;
        for(int i=0;i<k;i++) q.push({nums[i],i});
        ans.push_back(q.top().first);
        for(int i=k;i<n;i++){
            while(!q.empty()&&q.top().second<=i-k)
                q.pop();    //注意上面的等号，queue只能有(i-k,i]之间的数
            q.push({nums[i],i});
           ans.push_back(q.top().first);
        }
        return ans;
    }
};

标答双端队列

初始化双端队列dq和答案数组ans，在k个数以内如果之后的数比队尾大，那么把队尾的数弹出，之后加入（像单调栈一样，队列里的值是从大到小）ans[0]是队首的值，遍历剩下的数组，如果队首的序号超过范围里，把它弹出，如果新来的数比队尾大，那么把队尾的数弹出，最后更新答案

代码 Runtime190 ms Beats 90.70% Memory134.7 MB Beats 72.95%

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> q;vector<int>ans;//q里面放序号
        int n=nums.size();
        for(int i=0;i<k;i++){
            while(!q.empty()&&nums[q.back()]<=nums[i])q.pop_back();
            q.push_back(i);
        }
        ans.push_back(nums[q.front()]);
        for(int i=k;i<n;i++){
            if(q.front()<=i-k)q.pop_front();
            while(!q.empty()&&nums[q.back()]<=nums[i])q.pop_back();
            q.push_back(i);
            ans.push_back(nums[q.front()]);
        }
        return ans;
    }
};

标答左指针

初始化max_idx数组（模拟双端队列），ans数组，left指针，

注意如果直接vector<int> ans(n-k+1);来初始化ans，可以减少内存的使用

代码 Runtime 173 ms Beats 98.6 Memory 129.7 MB Beats 99.17%

class Solution {
public:
    int n;
    vector<int> max_idx;//array storing index for max
    int left=0;
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        n=nums.size();       
        vector<int> ans(n-k+1);
        for(int i=0;i<k;i++){
            while(max_idx.size()>left && nums[i]>=nums[max_idx.back()]) 
                max_idx.pop_back();// pop back the indexes for smaller ones
            max_idx.push_back(i);  // push back the index for larger one
        }
        ans[0]=nums[max_idx[left]];   
        for(int i=k; i<n; i++){
            while(max_idx.size()>left && nums[i]>=nums[max_idx.back()]) 
                max_idx.pop_back();// pop back the indexes for smaller ones
            max_idx.push_back(i);  // push back the index for larger one
            if (max_idx[left]==i-k) left++; 
            ans[i-k+1]=nums[max_idx[left]];     
        }
        return ans;
    }
};

240. Search a 2D Matrix II

题意：给一个行和列都升序的矩阵，找target是否在矩阵中

我的思路

和之前不一样的是最左边一列不是索引，所以要nlogm

代码 Runtime 184 ms Beats 21.13% Memory 14.8 MB Beats 88.10%

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n=matrix.size();int q=0;
        int m=matrix[0].size();
        for(int q=0;q<n;q++){
            int l=0,r=m-1;
            while(l<=r){
                int mid=(l+r)/2;
                if(matrix[q][mid]<target) l=mid+1;
                else if(matrix[q][mid]==target) return 1;
                else r=mid-1;
            }
        }
        return 0;
    }
};

标答

因为行从小到大排列，列也是从小到大排列，所以可以从左上角或者右上角开始找，假设从左下角开始找，找小的行--，找大的列++，O(n+m)

代码 Runtime88 ms Beats 72.75% Memory14.9 MB Beats 47.68%

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& ma, int tar) {
        int m=ma[0].size(),n=ma.size();
        int row=n-1,col=0;
        while(row>=0&&col<m){
            if(ma[row][col]>tar)row--;
            else if(ma[row][col]<tar)col++;
            else return 1;
        }
        return 0;
    }
};

神奇的优化在最后加上ma.clear()会使时间大幅度减少

试了试第215题，第131题是可行的，但第72题，第53题就不行

补充知识：STL中的隐性性能开销与副作用

代码 Runtime21 ms Beats 99.80% Memory14.9 MB Beats 47.68%

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& ma, int tar) {
        int m=ma[0].size(),n=ma.size();
        int row=n-1,col=0;
        while(row>=0&&col<m){
            if(ma[row][col]==tar){ma.clear();return 1;}
            if(ma[row][col]>tar)row--;
            else col++;
        }
        ma.clear();
        return 0;
    }
};

283. Move Zeroes

题意：把0都放在最后

我的思路

想过荷兰国旗算法，但是这样就把非0的顺序打乱了，所以不会做

标答

就是简单的思维题

代码 Runtime12 ms Beats 94.45% Memory19.2 MB Beats 34.86%

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int j=0;
        for(int i=0;i<nums.size();i++){
            if(nums[i])
                nums[j++]=nums[i];
        }
        for(;j<nums.size();j++)nums[j]=0;
        return ;
    }
};

287. Find the Duplicate Number

题意：一个数组，有一个数出现了多次，返回这个数

我的思路

开一个vis看有无重复；用上了取消同步和clear

代码 Runtime37 ms Beats 100% Memory61 MB Beats 98.76%

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        bool vis[100005]={0};
        ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
        for(int i=0;i<nums.size();i++){
            if(vis[nums[i]]){nums.clear();return nums[i];}
            vis[nums[i]]=1;
        }
        return -1;
    }
};

标答快慢指针

定义快指针和慢指针，就是看环的接口处以及之前值相同的地方

以1 3 3 4 2 为例

第一轮 fast=3(1) slow=1

第二轮 fast=2 slow=3

第三轮 fast=4 slow=4

fast=0

fast=1，slow=2

fast=3（1），slow=3(2)

例子

3 1 3 4 2

第一轮 fast=4 slow=3(1)

第二轮 fast=3(2)，slow=4

第三轮 fast=2，slow=2

fast=0

fast=3(1) slow=3(2)

代码 Runtime39 ms Beats 99.99% Memory 61 MB Beats 99.82%

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(0);
        int fast = 0; int slow = 0;
        while (true){
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(slow == fast){break;}
        }
        fast = 0;
        while(true){
            fast = nums[fast];
            slow = nums[slow];
            if(fast == slow){nums.clear();return slow;}
        }
    }
};

其他有趣的解法：LeetCode - The World's Leading Online Programming Learning Platform

改变数值不增加空间的：因为1 <= nums[i] <= n，nums.length == n + 1，所以数组中最大的数小于nums.size()，遍历数字，每遍历一个数nums[i]，就把nums[nums[i]]变成负的，这样如果遍历到nums[nums[i]]是负的，就返回nums[i]

二分查找、位运算……

295. Find Median from Data Stream

题意：返回中位数

我的思路

对顶堆

代码 Runtime276 ms Beats 74.61% Memory116.8 MB Beats 96.59%

class MedianFinder {
public:
    priority_queue<int,vector<int>,greater<int> >qs;//小的在最上面
    priority_queue<int,vector<int>,less<int> >qb;//大的在最上面
    MedianFinder() {}
    void addNum(int num) {
        if(qs.empty()&&qb.empty())qs.push(num);
        else if(qs.top()<num) qs.push(num);
        else qb.push(num);
        while(qs.size()-1>qb.size()){//4 3 or 3 3 or 3 4都可以
            int tmp=qs.top();qs.pop();qb.push(tmp);
        }
        while(qs.size()+1<qb.size()){
            int tmp=qb.top();qb.pop();qs.push(tmp);
        }
    }
    double findMedian() {
        int sn=qs.size(),bn=qb.size();
        if(sn<bn)return qb.top();
        else if(sn>bn)return qs.top();
        else return 1.0*(qs.top()+qb.top())/2;
    }
};

标答优化

上面的对顶堆写的有可以改进的地方

1. 维持qs比qb多一个的情况，不用循环【第一次进入的是qs，所以qs比qb多一个】

2. 有了上面的限定，奇数就只要返回qs的顶部就可以了

3. 不用创造变量tmp，直接qb.push(qs.top())放进去就可以了（不知道能否减少时间，但确实少了

以上3个方法在一起 Runtime 253 ms Beats 95.75%

4. 耍赖方法，ios::sync_with_stdio(0) Runtime 230 ms Beats 99.83% Memory 116.9 MB

代码 Runtime 253 ms Beats 95.75% Memory117 MB Beats 33.29%

class MedianFinder {
public:
    priority_queue<int,vector<int>,greater<int> >qs;//小的在最上面
    priority_queue<int,vector<int>,less<int> >qb;//大的在最上面
    MedianFinder() {}
    void addNum(int num) {
        if(qs.empty()||qs.top()<num)qs.push(num);
        else qb.push(num);
        if(qs.size()-1>qb.size()){//5 3 no
            qb.push(qs.top());qs.pop();
        }
        else if(qs.size()<qb.size()){//3 4-->4 3
            qs.push(qb.top());qb.pop();
        }
    }
    double findMedian() {
        int sn=qs.size(),bn=qb.size();
        if(sn!=bn)return qs.top();
        else return 1.0*(qs.top()+qb.top())/2;
    }
};

300. Longest Increasing Subsequence

题意：严格上升序列的长度

我的思路

动态规划，我记得还有用队列优化，二进制优化（？）和普通dp版本

但我都忘记了

例子一

num[i] 1 10 100 1000 10000 2 3 4 5 6 7 8

dp[i] 1 2 3 4 5 2 3 4 5 6 7 8

v[i] 0 0 1 2 3 0 5 6 7 8 9 10

例子二

num[i] 5 6 7 2 1 7 8 9 4

dp[i] 1 2 3 1 1 3 4 5 2

v[i] # 0 1 # # 1 2 6 3

v[i]要找dp最大的且比自己小的

开一个空间表示比自己小的位置在哪里v[i]，dp[i]=dp[v[i]]+1 最后遍历一遍，找个最大的 On^2 ?

---->(详见标答动态规划）

单调栈如何？单调栈5 6 7 2 部分，2会把所有数字都弹出的，不行

双端队列如何？如果比对头小，把对头弹出，加入；如果比队尾大，加入；例子一不行

vector如何？直接二分+插入，二分就用lower_bound

1 10 100 1000 10000

1 2 100 1000 10000

1 2 3 1000 10000

1 2 3 4 10000

1 2 3 4 5

1 2 3 4 5 6……可以

代码二分 Runtime7 ms Beats 90.93% Memory10.3 MB Beats 87.20%

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> v;
        for(int i=0;i<nums.size();i++){
            int tmp=lower_bound(v.begin(),v.end(), nums[i])-v.begin();
            if(tmp==v.size())v.push_back(nums[i]);
            else v[tmp]=nums[i];
        }
        return v.size();
    }
};

标答动态规划

初始化dp[0]为1；在[0, i]的序列中，从右向左看，如果nums[j]<nums[i]且dp[j]>dp[i]，dp[i]=dp[j];这一步就是上面思路中的v的代替品；最后循环结束，到dp[i]的时候++；

代码 Runtime 171 ms Beats 75.72% Memory10.3 MB Beats 97.68%

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();int dp[2505]={0};
        int ans=1;dp[0]=1;
        for(int i=1;i<n;i++){
            for(int j=i-1;j>=0;j--){//从i-1开始
                if(nums[j]<nums[i]&&dp[j]>dp[i])
                    dp[i]=dp[j];
            }
            dp[i]++;
            ans=max(ans,dp[i]);
        }
        return ans;
    }
};

标答树状数组

前置知识——树状数组是什么

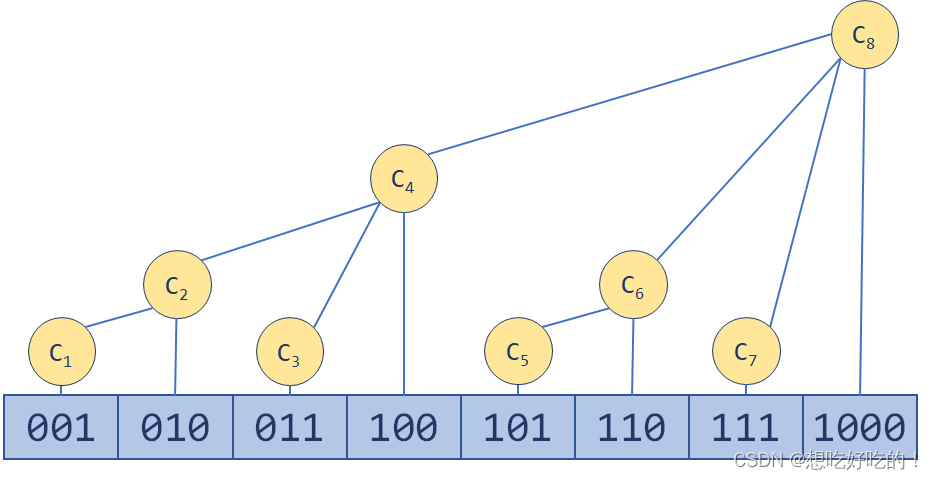
——来源：算法学习笔记(2) : 树状数组

树状数组思路

dp的第二层循环的目的是找小于等于num[i]的数字中dp[j]>dp[i]的

所以建立树状数组c[i]，其中i是num[i]，c[i]是dp[i]，从1开始

首先建树int c[maxn]，c[1]=1，如果query(i-1)>dp[i]，dp[i]=query(i-1)；dp[i]++，add(i, dp[i])

或者不要dp数组了，因为dp[i]刚刚遍历到为0，一定query(i-1)>dp[i]；之后的操作也没有dp[i-1]，所以可以省略

写完了发现nums[i]居然有负数，记得加上偏移量

代码 Runtime 4 ms Beats 95.80% Memory 10.3 MB Beats 87.20%

class Solution {
public:
    #define lowbit(x) x&(-x)
    int c[20004]={0};
    //c[1]不需要初始化为1
    int query(int a){//找[1,a]中最大的数
        int maxx=0;
        for(int i=a;i>0;i-=lowbit(i))
            maxx=max(maxx,c[i]);
        return maxx;
    }
    void add(int a,int k){
        for(int i=a;i<20004;i+=lowbit(i))
            c[i]=max(c[i],k);
    }
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();int ans=0;
        for(int i=0;i<n;i++){
            int ma=query(nums[i]-1+10001);//注意这里是nums[i]-1，比nums[i]小才可以
            add(nums[i]+10001,ma+1);
            ans=max(ans,ma+1);
        }
        return ans;
        //因为你不知道数组nums中最大的数m是多少（除非你遍历一遍）
        //所以你不能return query(m)
        //所以一边遍历一边更新答案
    }
};

322. Coin Change

题意：给你硬币类型和目标，求最少的硬币数

我的思路

不知道贪心行不行，所以就用动态规划了

1. 初始化为负无穷来判断安排是否合法

2. 求最小的时候要多一步条件判断

代码 Runtime 59 ms Beats 87.21% Memory9.9 MB Beats 98.52%

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int dp[10004];
        memset(dp,-0x3f,sizeof(dp)); dp[0]=0;
        int m=coins.size();
        for(int i=0;i<=amount;i++){
            for(int j=0;j<m;j++){
                if(i>=coins[j]&&dp[i-coins[j]]>=0){
                    if(dp[i]<0)
                        dp[i]=dp[i-coins[j]]+1;
                    else    
                        dp[i]=min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        if(dp[amount]<0)return -1;
        return dp[amount];
    }
};

标答递归+贪心+记忆化但是没懂

最前面的条件判断：如果amount是双数，但是coin里面没有双数就返回-1；硬币从小到大排序；

接下来看注解，总之是很精密的代码

就是有一个地方不懂，如果没有一开始的if判断，它会超时

那有无可能存在一个不被最开始的if检测到的-1情况会使这个代码超时？

代码 Runtime3 ms Beats 99.98% Memory9.9 MB Beats 99.78%

class Solution{
bool check(vector<int>& coins, short index, int cnt, int target){
        long sum = (long) coins[index]*cnt;//相乘可能超出int的范围
        if (sum==target) return true;//如果数量刚好，就是可以用cnt个硬币
        else if (sum > target) {//如果sum超过了，就要换个计划
            if (index == 0) return false;//没有剩下的硬币类型了，不可能了
            for (short i = cnt; i>0; i--){//预计给之后的硬币类型 i个来搞定，自己留下cnt-i个
                long take = target - (long)coins[index]*(cnt-i);
                //take是预计之后的硬币类型要达成的数量
                //为什么cnt-i会==0，因为可能不用这个硬币
                if (take < 0) break;
    //为什么自己留下的cnt-i要从小到大遍历？因为cnt-i大了，take小于0，更大的cnt-i就更不用看了
                int r =  take;//隐性的类型转换也要时间，所以这里多一步
                if (check(coins, index-1, i, r)) return true;    
            }
        }
        return false;
    }
public:
    int coinChange(vector<int>& coins, int amt) {
        if (amt&1){//如果是双数
            short i=0;
            for (;i<coins.size();i++){
                if(coins[i]&1)break;
            }
            if (i==coins.size()) return -1;  
        }
        sort(coins.begin(), coins.end());
        int best = amt/coins.back();//个数最少的
        int worst = amt/coins.front();//个数最多的
        for(short i=best; i<=worst;i++)//预计i个硬币
            if (check(coins, coins.size()-1, i, amt)) 
                return i;
        return -1;
    }
};

347. Top K Frequent Elements

题意：返回k个出现次数最多的数

我的思路

哈希，nlogn

map默认是按key值从小到大排序的，不能更改sort方式，所以用vector<pii>的方式了

遇到的问题：错误解决方法：error: reference to non-static member function must be called

要在cmp函数前面加上static

代码 Runtime 8 ms Beats 93.30% Memory13.7 MB Beats 59.82%

class Solution {
public:
    # define pii pair<int,int> 
     static bool cmp(pii &a,pii &b){
        return a.first>b.first;
    }
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int,int>mp;
        vector<pii> cnt; vector<int> ans;
        int n=nums.size();
        for(int i=0;i<n;i++)
            mp[nums[i]]++;
        for(auto&q:mp) 
            cnt.push_back({q.second,q.first});
        sort(cnt.begin(),cnt.end(),cmp);
        for(int i=0;i<k;i++)
            ans.push_back(cnt[i].second);
        return ans;
    }
};

标答是map+优先队列，我觉得差不多