目录
一,目标和
1.题意
2.例子
3.题目接口
4.解题思路及代码
二,组合总和
1.题意
2.例子
3.题目接口
4.解题思路及代码
三,字母大小写全排列
1.题意
2.例子
3.题目接口
4.解题思路及代码
一,目标和
1.题意
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加
'+'或'-',然后串联起所有整数,可以构造一个 表达式 :例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。
2.例子
3.题目接口
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
}
};4.解题思路及代码
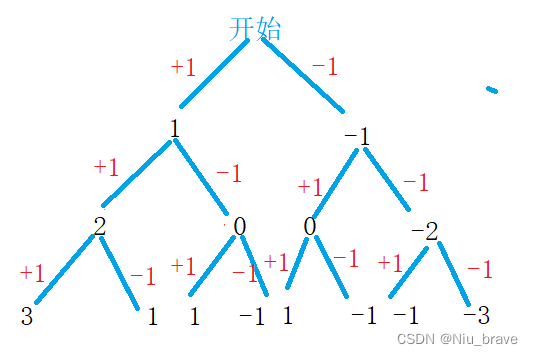
举个例子:如果我的数组里面有三个1,我要得到运算结果为1的组合。我们该如何操作呢?画出决策树如下:
从这张图里面我们可以看到,这里只要深度优先搜索就行了。那什么时候回退到上一层呢?答案显而易见,只有走到最后一层才能回退。函数体应该怎么写呢?关注节点,可知道我们在一个节点上有两种选择。别的不说先写代码如下:
class Solution { public: int count;//记录符合条件的情况 int path;//记录路径上的和 int findTargetSumWays(vector<int>& nums, int target) { dfs(nums,target,0); return count; } void dfs(vector<int>& nums, int target,int pos) { if(pos == nums.size()) { if(path == target) { count++; } return; } path+=nums[pos];//加的情况 dfs(nums,target,pos+1); path-=nums[pos]; path-=nums[pos];//减的情况 dfs(nums,target,pos+1); path+=nums[pos]; } };这是一个采用了全局变量的写法,但是你会发现这玩意过不了:
所以,我们就得改变一下策略了。这个时候我们就不能用全局变量了,而是改用参数变量,代码如下:
class Solution { public: int count;//记录符合条件的情况 int findTargetSumWays(vector<int>& nums, int target) { dfs(nums,target,0,0); return count; } void dfs(vector<int>& nums, int target,int pos,int path) { if(pos == nums.size()) { if(path == target) { count++; } return; } dfs(nums,target,pos+1,path+nums[pos]);//加的情况 dfs(nums,target,pos+1,path-nums[pos]);//减的情况 } };这样代码就过掉了:
为什么将path变成函数参数后便能过呢?其实原因就是将path改为dfs的参数以后就能够减少+,-的运算了。加减运算在运行时可是很耗时间的。
二,组合总和
1.题意
给你一个 无重复元素 的整数数组
candidates和一个目标整数target,找出candidates中可以使数字和为目标数target的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。对于给定的输入,保证和为
target的不同组合数少于150个。
2.例子
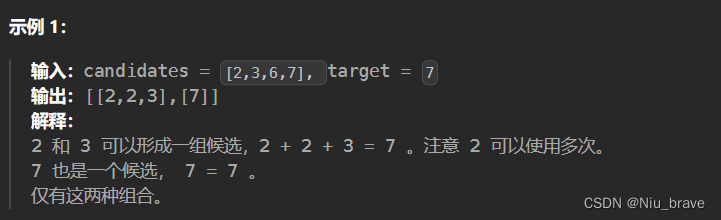
3.题目接口
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
}
};4.解题思路及代码
其实这道题和前面我们见过的那道全排列的题的思路差不多。但是,不同点在于:
1.在这道题里面我们每一组的个数是不定的,只要找出的数组值的和可以等于目标值。
2.在这道题里的同一条路径里的同一个数可以重复使用,但是在一条路劲里使用了以后另一条路劲就不能再使用了。
在这里再来说一下递归的结束条件,当加到的和大于或者等于target的时候便可以收网返回了。所以写出的代码如下:
class Solution { public: vector<int>path; vector<vector<int>>ret; int aim;//来一个aim来作target的全局变量 int sum;//计算路径上的数值的和 vector<vector<int>> combinationSum(vector<int>& candidates, int target) { aim = target;//给aim赋值 dfs(candidates,0); return ret; } void dfs(vector<int>&candidates,int pos) { if(sum==aim) { ret.push_back(path); return; } if(sum>aim) { return; } for(int i = pos;i<candidates.size();i++)//当同一层有多个树要遍历时便可以使用for循环 { sum+=candidates[i]; path.push_back(candidates[i]); dfs(candidates,i);//下一层还是从当前位置开始遍历 sum-=candidates[i]; path.pop_back(); } } };
三,字母大小写全排列
1.题意
给定一个字符串
s,通过将字符串s中的每个字母转变大小写,我们可以获得一个新的字符串。返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。
2.例子
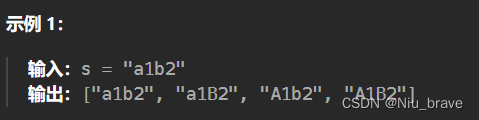
3.题目接口
class Solution {
public:
vector<string> letterCasePermutation(string s) {
}
};4.解题思路及代码
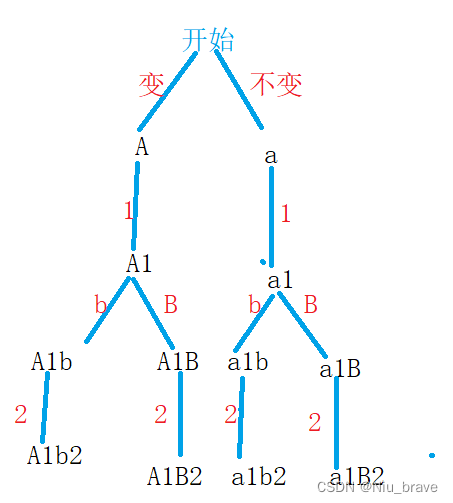
首先举个例子,比如s = "a1b2"。先画出决策树如下:
首先,从这个决策树里面可以判断的是我们不会遇到一层要把所有的树遍历一遍的情况。但是在遇到字母时又要考虑两种情况也就是会遇到大小写字母转换的问题。我们的递归结束条件就是当我们每一个path里的节点个数等于原数组时便要结束条件返回到上一层。根据这个思想写出的代码如下:
class Solution { public: string path;//记录路径节点 vector<string>ret;//记录每一条路径 vector<string> letterCasePermutation(string s) { dfs(s,0); return ret; } void dfs(string& s,int pos) { if(path.size()==s.size()) { ret.push_back(path); return; } //不变的情况 char ch = s[pos];//记录一下,因为元素会在后面被删除掉 path.push_back(s[pos]); dfs(s,pos+1); path.pop_back(); //变的情况 if(ch>'9'||ch<'0') { char tmp = change(ch); path.push_back(tmp); dfs(s,pos+1); path.pop_back(); } } char change(char& ch)//大小写转换函数 { if(ch>='a'&&ch<='z') { ch = ch-32; } else { ch = ch+32; } return ch; } };