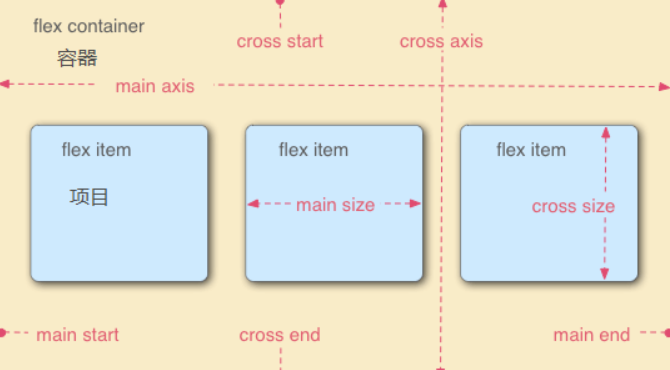
文章目录
- 前言
- 一、小批量梯度下降 mini-batch
- 1、batch gradient descent
- 2、stochastic gradient descent
- 3、mini-batch gradient descent
- 二、指数加权平均
- 1.什么是指数加权平均
- 2、理解指数加权平均
- 3、与普通求平均值的区别
- 4、指数加权平均的偏差修正
- 三、gradient descent with momentum
- 四、RMSprop
- 五、适应性矩估计 Adam
- 六、学习率衰减
- 七、局部最优解问题。
前言
一、小批量梯度下降 mini-batch
如果一个数据集有500w个数据,那我们迭代一次花费的时间就太久,且对所有训练集遍历一次也只是梯度逼近一步,但如果我们采用小批量梯度下降,大小为1000,那我们每迭代一次在1000个数据上就能逼近w一步,迭代完所有数据就梯度逼近5000步,能够提高效率。

向前传播 损失函数的计算 向后传播都要相应改变。
1、batch gradient descent
如果 mini-batch size=m
则就相当于普通的梯度下降了。
如果数据集不大的情况下,这是一种好的算法。一般而言<2000
2、stochastic gradient descent
随机梯度下降
如果 mini-batch size=1
这时候我们便失去了矢量化使计算加速的优点了
因为每次只有一个样本。
3、mini-batch gradient descent
如果 1<mini-batch size<m
我们一般取2的n次方,与计算机存储有关,一般取64-512
这样的好处是:既可以使用矢量计算的好处
又可以不必每次在所有数据遍历完一遍之后在梯度逼近
二、指数加权平均
exponentially weighted averages
1.什么是指数加权平均
这里以温度为例
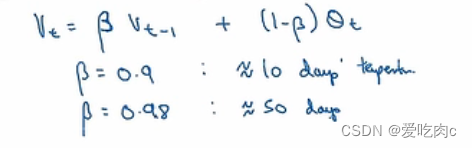
Vt 为加权后的温度,
theta t:是当天的真实温度
β:是系数,也相当于一个超参数,一般取0.9
当β=0.9时,我们说取的近似是10的平均温度。
1/1-β。
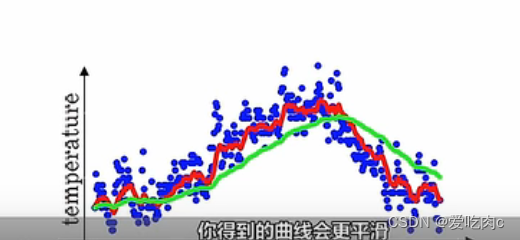
红色是β=0.9
绿色是β=0.98
我们可以看出β=0.98时,绿色线向右移动,
通过公式我们可以看出,那是因为之前的权重变大了而当天的权重减小了。
2、理解指数加权平均
 对于V100 我们可以一步一步拆解开来,可以看到对于每天的温度都有不同的权重。
对于V100 我们可以一步一步拆解开来,可以看到对于每天的温度都有不同的权重。
0.9的10次方≈1/e 约等于最大值的三分之一
即当10天之后的温度会下降到最大权重的三分之一,可以忽略。
即就相当于β=0.9时,我们相当于计算的是10天的平均气温。
3、与普通求平均值的区别
①普通求平均值我们都是相当于一样的权值,比如语文100,数学99,英语98。那么三科平均值就是99.
但是对于指数平均我们相当于给了不同的值不同的权重,例如温度,我们肯定是离今天近的权重大,离今天太远的,我们可以忽略。
②代码简单,且需要的存储空间小。
比如想要求n天的平均值,那么我们只要有前n-1天的值和当天的值即可,
若是普通求平均值,则需要把n天的值都存储起来。
4、指数加权平均的偏差修正
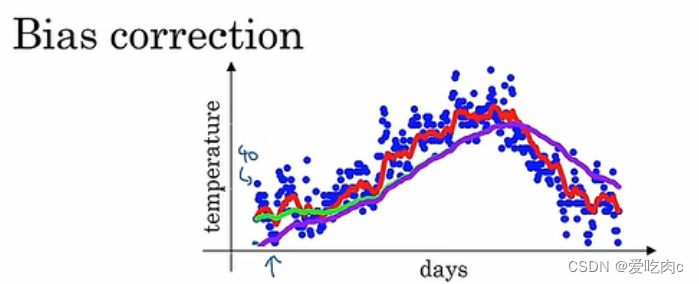
当β=0.98时,我们实际得到的是紫色这条线
刚开始V0=0
V1=βV0+(1-β)θ1 =0.02θ1
V2=0.980.02*θ1+0.02θ2
因为前面的系数太小,所以导致V1,V2这些得到的并不是前几天的平均值。
比平均值小。
但是当往后时,迭代次数增多之后,紫色与绿色线几乎重合。
所以在批量梯度下降时,由于迭代次数多,所以几乎可以不用偏差修正。
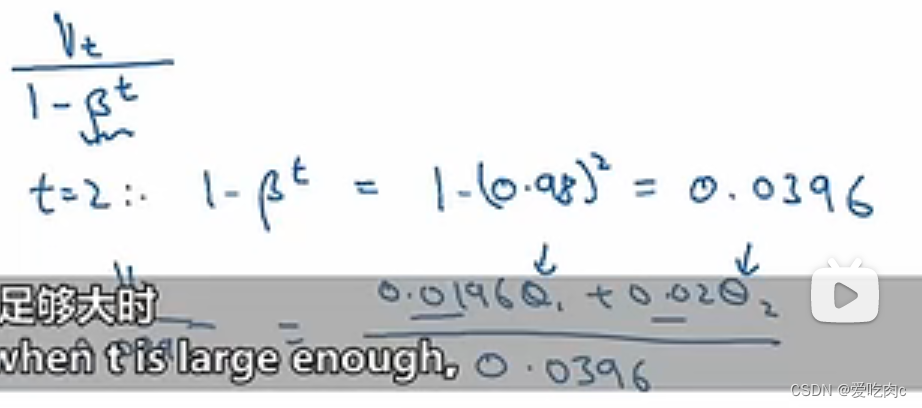
我们可以采用第一个公式进行偏差修正,当t很大时,βt≈0,此时紫色与绿色线又几乎重合。
三、gradient descent with momentum

一般的 对于我们的梯度下降算法来说,如果我们的学习率太小,迭代一次效率就会过低,但是如果学习率太大,就会造成我们的损失函数并没有朝着 减小的方向前进。
我们既希望在水平方向上朝着最小值前进,又希望在垂直方向上不要太过跌宕。
动量梯度下降
我们采用了指数加权平均的方法
如果我们的学习率过大,我们在垂直方向上可能如图:

虽然水平方向上一直还是沿着最小值,但是水平方向可能太过跌宕,如下图绿色线。

画的太丑 可以忽略。不过我觉得这个更直观
红色的是我们希望的 水平方向沿着最小值前进 且垂直方向不会太跌宕
采用了指数加权平均后,我们在垂直方向上的平均值就会平缓许多,平且在水平方向上还是沿着最小值方向前进。
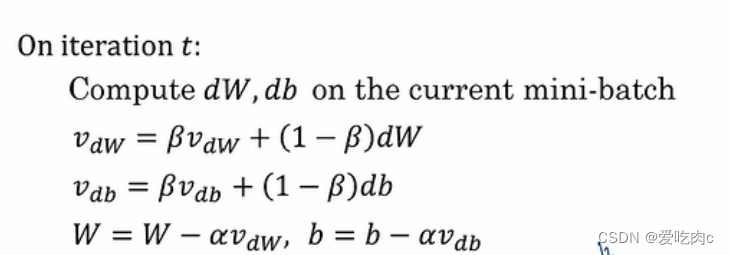
吴老师这个公式我觉得不太对…公式右边为什么还是Vdw呢?那移到左边不是可以抵消了吗?心存疑惑…希望知道的可以解答一下~~
四、RMSprop
root mean square prop

我们希望在垂直方向上数值不要太大,水平方向上数值不要太小。
在垂直方向上 的值会过大,db也就会大,相对而言水平方向的值小。
除以之后就会变化,w会大,b会小。
rmsprop 和动量梯度一样可以降低我们梯度下降中的震荡,同时使我们可以以一个大的学习率α,从而提高算法的效率。
五、适应性矩估计 Adam

Adam结合了动量梯度下降和RMSprop的好处。
Adam一般都需要偏差修正!!!
超参数:

六、学习率衰减
learning rate decay

蓝色:是我们学习率固定时,由于学习率固定,在最后阶段我们在最小值周围绕,且这个范围较大。
此时,如我们采取学习率衰减,刚开始仍能以较大的步长梯度下降,最后我们可以以小的步长来接近最小值。如绿色。
学习率衰减的公式:

dacay-rate是一个超参数。
其他公式:

t是批处理中 批处理的t,每一次遍历中学习率α都随t的变化而变化,并且每次遍历都与之前遍历的α相同。就导致如左下图的学习率。
七、局部最优解问题。
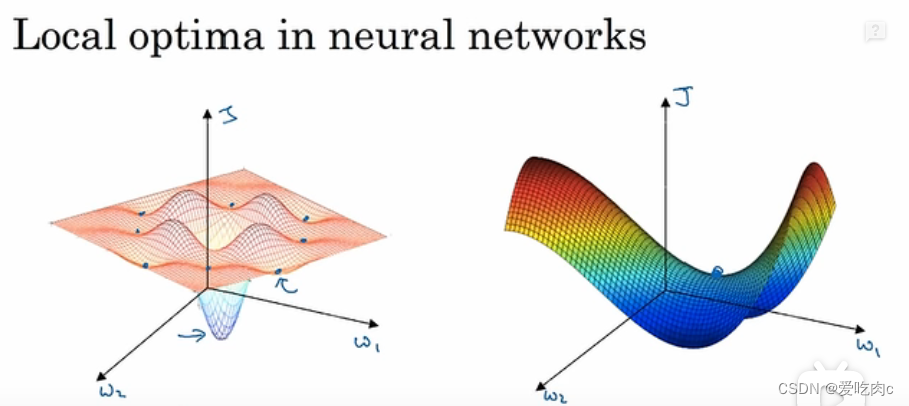
比如左边图,这是一个低维图,我们很容易可以看出这个图有很多局部最优,而不是全局最优。
但是对于高维图,这种局部最优是很难的,它需要每一个方向上都是凹函数,对于一个200维的,这种局部最优概率是1/2的200平方。
所以对于高维图,是很难出现多个局部最优的,出现的大多都是右图这种,叫做鞍点。
每个方向的凹凸不一定都一致,这不是局部最优点。
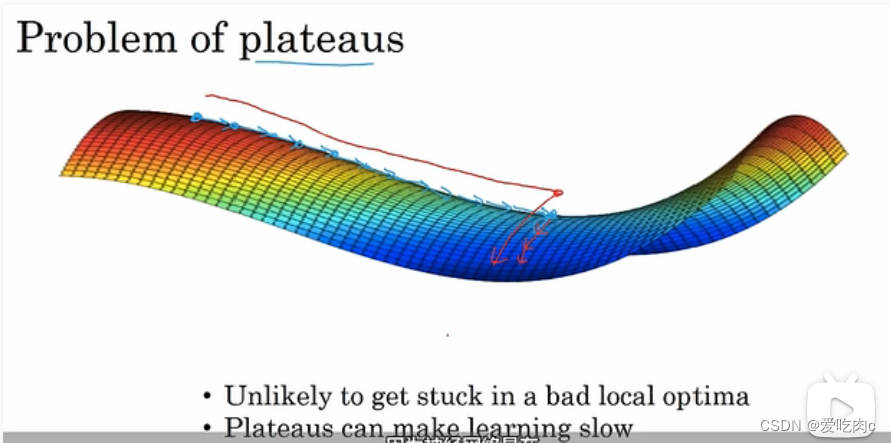
对于高维我们要解决的不是多个局部最优的问题,更应该解决的是停滞区的问题,梯度逼近太慢。
但是通过adam和动量梯度下降可以解决这个问题。

![[附源码]Python计算机毕业设计公司办公自动化系统Django(程序+LW)](https://img-blog.csdnimg.cn/8b98ec712c304b919f6e94b3f2e0c24b.png)