使用TensorFlow完成线性回归

1. 导入TensorFlow库

# 导入相关库
%matplotlib inline
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

2. 构造数据集

# 产出样本点个数
n_observations = 100
# 产出-3~3之间的样本点
xs = np.linspace(-3, 3, n_observations) 
# sin扰动
ys = np.sin(xs) + np.random.uniform(-0.5, 0.5, n_observations) 

xs

array([-3. , -2.93939394, -2.87878788, -2.81818182, -2.75757576,
-2.6969697 , -2.63636364, -2.57575758, -2.51515152, -2.45454545,
-2.39393939, -2.33333333, -2.27272727, -2.21212121, -2.15151515,
-2.09090909, -2.03030303, -1.96969697, -1.90909091, -1.84848485,
-1.78787879, -1.72727273, -1.66666667, -1.60606061, -1.54545455,
-1.48484848, -1.42424242, -1.36363636, -1.3030303 , -1.24242424,
-1.18181818, -1.12121212, -1.06060606, -1. , -0.93939394,
-0.87878788, -0.81818182, -0.75757576, -0.6969697 , -0.63636364,
-0.57575758, -0.51515152, -0.45454545, -0.39393939, -0.33333333,
-0.27272727, -0.21212121, -0.15151515, -0.09090909, -0.03030303,
0.03030303, 0.09090909, 0.15151515, 0.21212121, 0.27272727,
0.33333333, 0.39393939, 0.45454545, 0.51515152, 0.57575758,
0.63636364, 0.6969697 , 0.75757576, 0.81818182, 0.87878788,
0.93939394, 1. , 1.06060606, 1.12121212, 1.18181818,
1.24242424, 1.3030303 , 1.36363636, 1.42424242, 1.48484848,
1.54545455, 1.60606061, 1.66666667, 1.72727273, 1.78787879,
1.84848485, 1.90909091, 1.96969697, 2.03030303, 2.09090909,
2.15151515, 2.21212121, 2.27272727, 2.33333333, 2.39393939,
2.45454545, 2.51515152, 2.57575758, 2.63636364, 2.6969697 ,
2.75757576, 2.81818182, 2.87878788, 2.93939394, 3. ])

ys

array([-0.62568008, 0.01486274, -0.29232541, -0.05271084, -0.53407957,
-0.37199581, -0.40235236, -0.80005504, -0.2280913 , -0.96111433,
-0.58732159, -0.71310851, -1.19817878, -0.93036437, -1.02682804,
-1.33669261, -1.36873043, -0.44500172, -1.38769079, -0.52899793,
-0.78090929, -1.1470421 , -0.79274726, -0.95139505, -1.3536293 ,
-1.15097615, -1.04909201, -0.89071026, -0.81181765, -0.70292996,
-0.49732344, -1.22800179, -1.21280414, -0.59583172, -1.05027515,
-0.56369191, -0.68680323, -0.20454038, -0.32429566, -0.84640122,
-0.08175012, -0.76910728, -0.59206189, -0.09984673, -0.52465978,
-0.30498277, 0.08593627, -0.29488864, 0.24698113, -0.07324925,
0.12773032, 0.55508531, 0.14794648, 0.40155342, 0.31717698,
0.63213964, 0.35736413, 0.05264068, 0.39858619, 1.00710311,
0.73844747, 1.12858026, 0.59779567, 1.22131999, 0.80849061,
0.72796849, 1.0990044 , 0.45447096, 1.15217952, 1.31846002,
1.27140258, 0.65264777, 1.15205186, 0.90705463, 0.82489198,
0.50572125, 1.47115594, 0.98209434, 0.95763951, 0.50225094,
1.40415029, 0.74618984, 0.90620692, 0.40593222, 0.62737999,
1.05236579, 1.20041249, 1.14784273, 0.54798933, 0.18167682,
0.50830766, 0.92498585, 0.9778136 , 0.42331405, 0.88163729,
0.67235809, -0.00539421, -0.06219493, 0.26436412, 0.51978602])

# 可视化图长和宽
plt.rcParams["figure.figsize"] = (6,4)
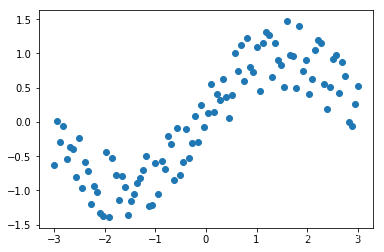
# 绘制散点图
plt.scatter(xs, ys) 
plt.show()

3. 定义基本模型

# 占位
X = tf.placeholder(tf.float32, name='X')
Y = tf.placeholder(tf.float32, name='Y')

# 随机采样出变量
W = tf.Variable(tf.random_normal([1]), name='weight') 
b = tf.Variable(tf.random_normal([1]), name='bias')

# 手写y = wx+b
Y_pred = tf.add(tf.multiply(X, W), b) 

# 定义损失函数mse
loss = tf.square(Y - Y_pred, name='loss') 

# 学习率
learning_rate = 0.01
# 优化器，就是tensorflow中梯度下降的策略
# 定义梯度下降,申明学习率和针对那个loss求最小化
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) 

4. 训练模型

# 去样本数量
n_samples = xs.shape[0]
init = tf.global_variables_initializer()
with tf.Session() as sess:
    # 记得初始化所有变量
    sess.run(init) 
    writer = tf.summary.FileWriter('../graphs/linear_reg', sess.graph)
    # 训练模型
    for i in range(50):
        #初始化损失函数
        total_loss = 0
        for x, y in zip(xs, ys):
            # 通过feed_dic把数据灌进去
            _, l = sess.run([optimizer, loss], feed_dict={X: x, Y:y}) #_是optimizer的返回，在这没有用就省略
            total_loss += l #统计每轮样本的损失
        print('Epoch {0}: {1}'.format(i, total_loss/n_samples)) #求损失平均

    # 关闭writer
    writer.close() 
    # 取出w和b的值
    W, b = sess.run([W, b]) 

Epoch 0: [0.48447946]
Epoch 1: [0.20947962]
Epoch 2: [0.19649307]
Epoch 3: [0.19527708]
Epoch 4: [0.19514856]
Epoch 5: [0.19513479]
Epoch 6: [0.19513334]
Epoch 7: [0.19513316]
Epoch 8: [0.19513315]
Epoch 9: [0.19513315]
Epoch 10: [0.19513315]
Epoch 11: [0.19513315]
Epoch 12: [0.19513315]
Epoch 13: [0.19513315]
Epoch 14: [0.19513315]
Epoch 15: [0.19513315]
Epoch 16: [0.19513315]
Epoch 17: [0.19513315]
Epoch 18: [0.19513315]
Epoch 19: [0.19513315]
Epoch 20: [0.19513315]
Epoch 21: [0.19513315]
Epoch 22: [0.19513315]
Epoch 23: [0.19513315]
Epoch 24: [0.19513315]
Epoch 25: [0.19513315]
Epoch 26: [0.19513315]
Epoch 27: [0.19513315]
Epoch 28: [0.19513315]
Epoch 29: [0.19513315]
Epoch 30: [0.19513315]
Epoch 31: [0.19513315]
Epoch 32: [0.19513315]
Epoch 33: [0.19513315]
Epoch 34: [0.19513315]
Epoch 35: [0.19513315]
Epoch 36: [0.19513315]
Epoch 37: [0.19513315]
Epoch 38: [0.19513315]
Epoch 39: [0.19513315]
Epoch 40: [0.19513315]
Epoch 41: [0.19513315]
Epoch 42: [0.19513315]
Epoch 43: [0.19513315]
Epoch 44: [0.19513315]
Epoch 45: [0.19513315]
Epoch 46: [0.19513315]
Epoch 47: [0.19513315]
Epoch 48: [0.19513315]
Epoch 49: [0.19513315]

print(W,b)
print("W:"+str(W[0]))
print("b:"+str(b[0]))

[0.23069778] [-0.12590201]
W:0.23069778
b:-0.12590201

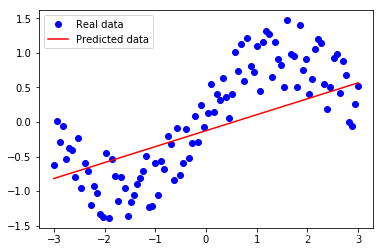
5. 线性回归图

# 线性回归图
plt.plot(xs, ys, 'bo', label='Real data')
plt.plot(xs, xs * W + b, 'r', label='Predicted data')
plt.legend()
plt.show()