文章目录
- 前言
- 一、62.不同路径
- 二、63.不同路径II
- 总结
前言
动态规划
一、62.不同路径
- 深搜
- 动态规划
- 数论
深搜:
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
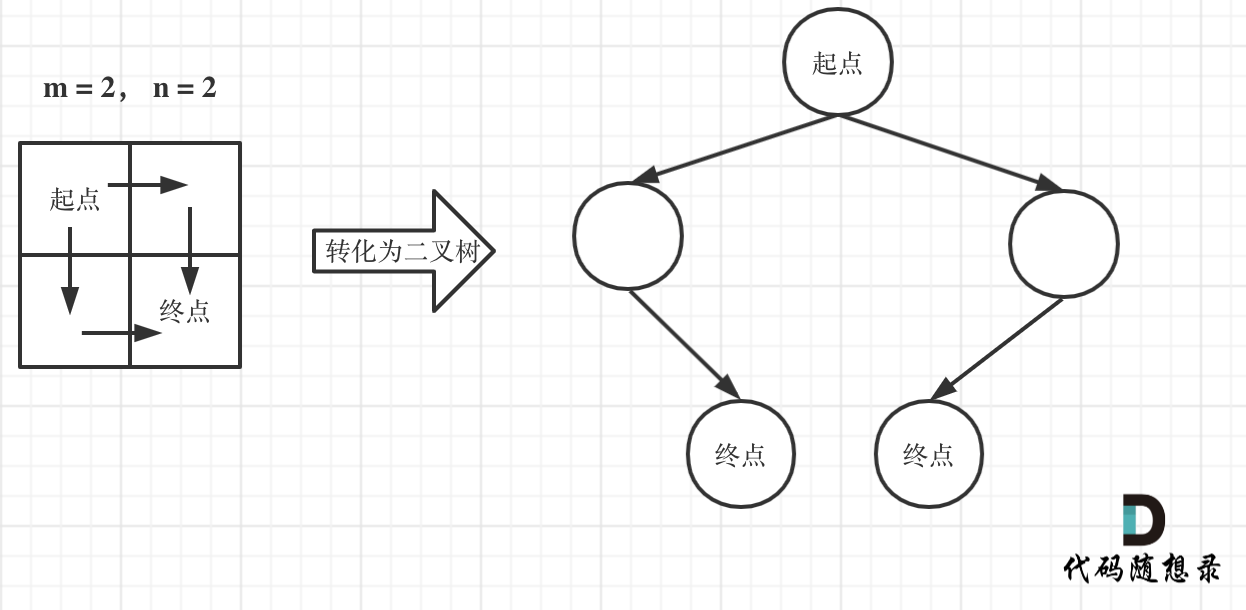
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:
int dfs(int i, int j, int m, int n) {
if (i > m || j > n) return 0; // 越界了
if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
}
public:
int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);
}
};
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
动态规划:
- 定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
- 举例推导dp数组
如图所示:
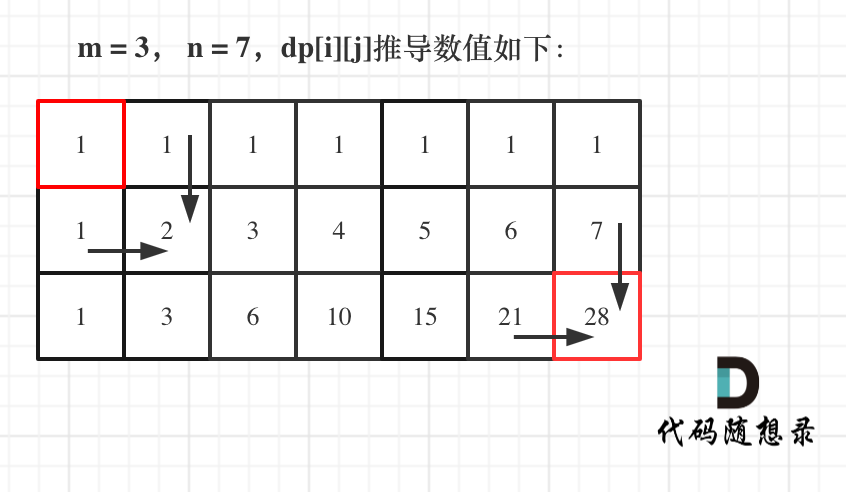
代码:
class Solution {
public int uniquePaths(int m, int n) {
int dp[][] = new int[m][n];
for(int i = 0;i<m;i++){
dp[i][0] = 1;
}
for(int j = 0;j<n;j++){
dp[0][j] = 1;
}
for(int i = 1;i<m;i++){
for(int j = 1;j<n;j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}数论:
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
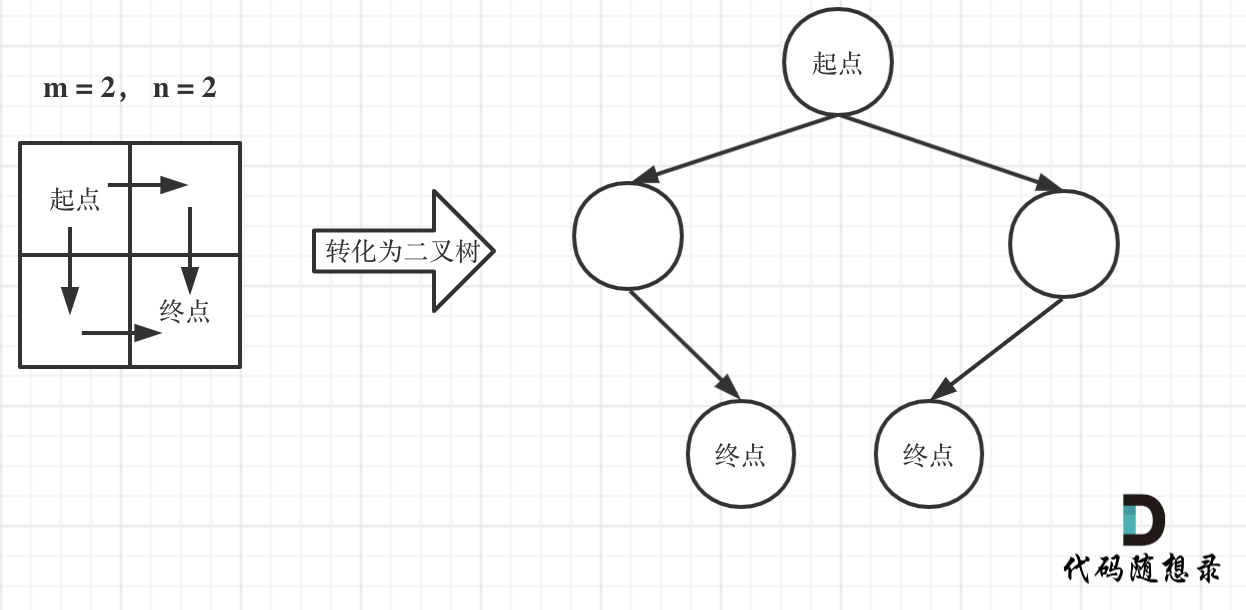
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。

求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
二、63.不同路径II
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
在62.不同路径
(opens new window)不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
如图:
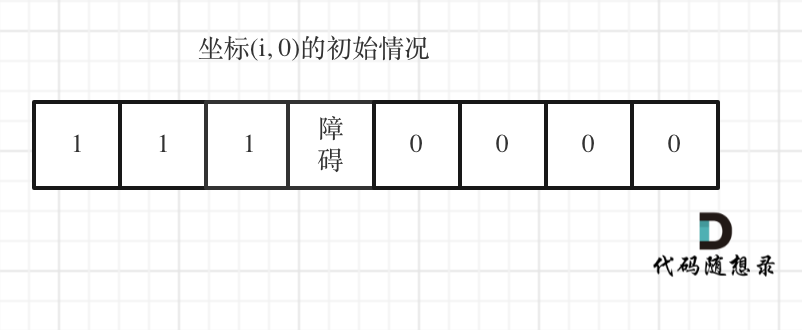
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
- 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
- 举例推导dp数组
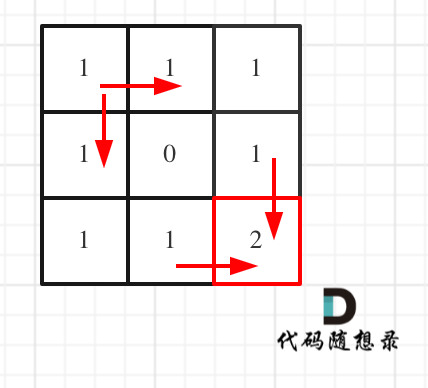
拿示例1来举例如题:
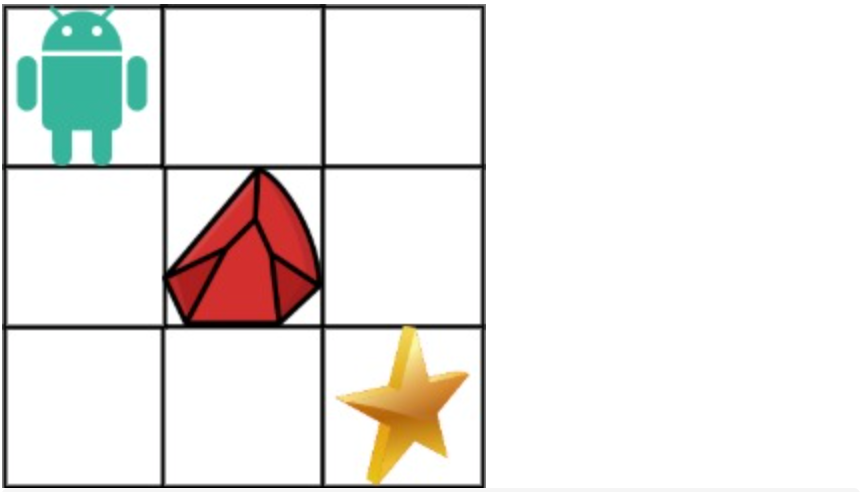
对应的dp table 如图:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int dp[][] = new int[m][n];
if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1){
return 0;
}
for(int i = 0;i<m && obstacleGrid[i][0] ==0;i++){
dp[i][0] = 1;
}
for(int i = 0;i<n && obstacleGrid[0][i] ==0;i++){
dp[0][i] = 1;
}
for(int i = 1;i<m;i++){
for(int j =1;j<n;j++){
if(obstacleGrid[i][j] ==0){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}else{
dp[i][j] = 0;
}
}
}
return dp[m-1][n-1];
}
}
总结
今天去看《奥本海默》。




![[Linux]套接字通信](https://img-blog.csdnimg.cn/8f49149f69d44df98f78bff0cdc6beeb.png)