摘要
我们使用扩散概率模型提出了高质量的图像合成结果,这是一类latent variable模型,灵感来自非平衡热力学。我们最好的结果是通过训练weighted variational bound ,根据新颖的连接扩散概率模型和去噪分数匹配朗之万动力学进行设计,而且我们的模型自然admit一个渐进的lossy decompression scheme,可以解释为autoregressive decoding的泛化。
假设图像符合高斯分布?
我们使用q想表达的p是?如何表达?这里的pq就是前向传播和逆向传播吗?为什么要用前向传播拟合逆向传播?
猜测:难道说,我们是想拟合出每一个xt?是想把前向传播和逆向传播的每一个节点都对齐?
weighted variational bound \ autoregressive decoding \ VAE \ autoregressive model
什么是变分推断?variational inference
首先,我们的原始目标是,需要根据已有数据推断需要的分布p;当p不容易表达,不能直接求解时,可以尝试用变分推断的方法, 即,寻找容易表达和求解的分布q,当q和p的差距很小的时候,q就可以作为p的近似分布,成为输出结果了。在这个过程中,我们的关键点转变了,从“求分布”的推断问题,变成了“缩小距离”的优化问题。举生活中的例子太难了,还是看图说话容易些
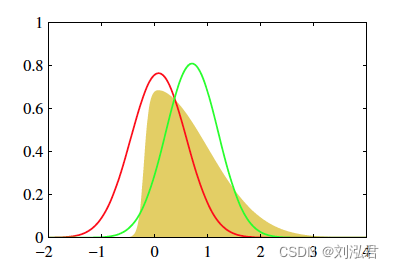
黄色的分布是我们的原始目标p,不好求。它看上去有点像高斯,那我们尝试从高斯分布中找一个红q和一个绿q,分别计算一下p和他们重叠部分面积,选更像p的q作为p的近似分布
1. 介绍

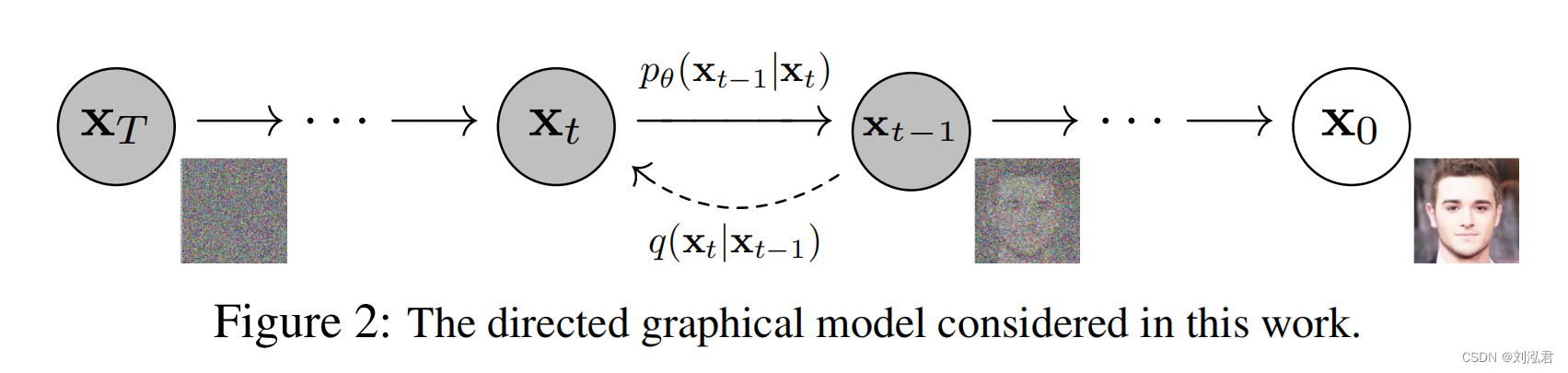
- 扩散模型是一个马尔科夫链;当扩散包含少量的高斯噪声时,将采样链转换设置为条件高斯噪声就足够了,允许一个特别简单的神经网络参数化。
- 能生成高质量照片。
- 此外,我们还证明了扩散模型的一些参数化揭示了在训练过程中denoising score matching over multiple noise levels during training和 annealed Langevin dynamics during sampling的等价性。
每个状态x都是latent
2. 背景
逆过程可以被定义为一个,可学习的Gaussian transition
这里Gausssian transition没搜到指的是啥,我理解的是从一个高斯分布,变成了另一个高斯分布;其中pθ中的μθ就是可学习的参数,有的论文里把方差也设置成可学习。
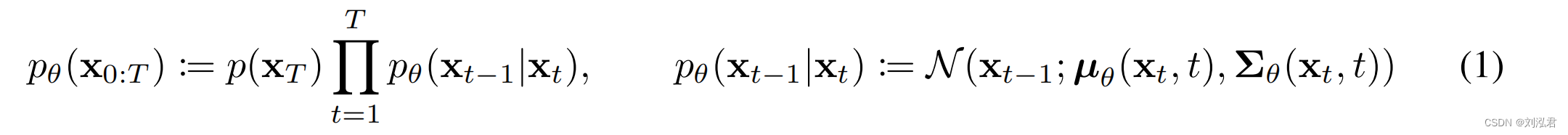
训练的损失函数为:Training is performed by optimizing the usual variational bound on negative log likelihood:
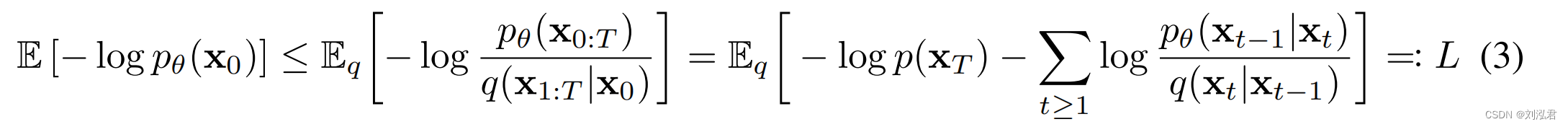
正向过程的一个值得注意的特性是,它允许在任意时间步长t以封闭形式采样:
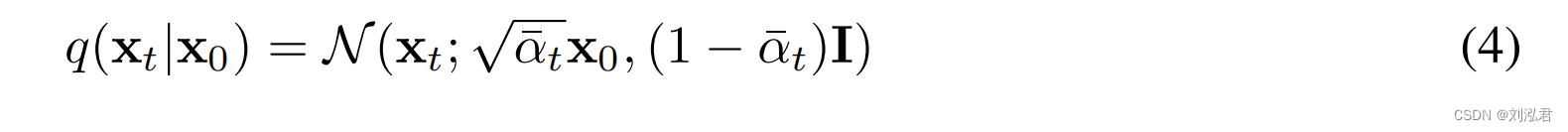
因此,通过使用随机梯度下降来优化L的随机项,可以进行有效的训练。进一步的改进来自于通过改写L (3)来减少方差:
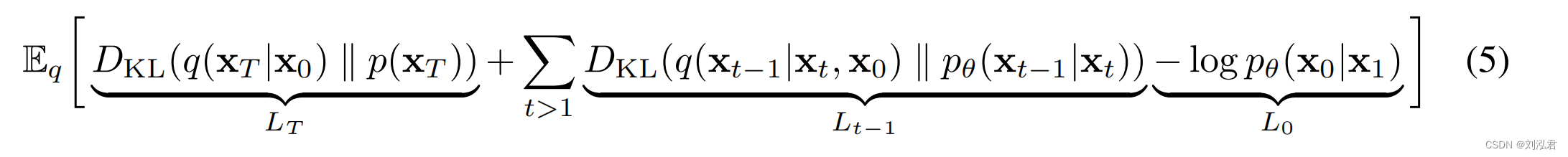
式(5)使用KL散度直接比较pθ(xt−1|xt)与前向过程后端,这在x0条件下是可处理的:
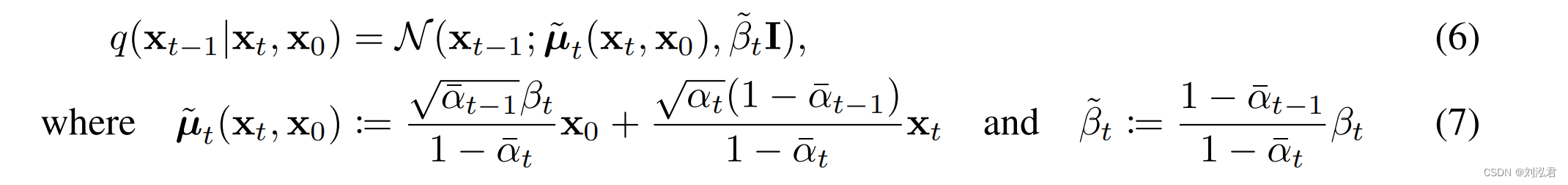
因此,等式中的所有KL差异(5)是高斯分布之间的比较,因此它们可以用封闭形式表达式的Rao-Blackwellized fashion计算,而不是高方差蒙特卡罗估计。
3. 方法
为了guide our choice,我们在扩散模型和denoise score matching之间建立了一个新的显式联系,成功添加了扩散模型的一个简化的variational bound objective。
our choice 指的是?
denoise score matching 指的是?
variational bound objective指的是?
“此外,我们还证明了扩散模型的一定参数化揭示了在训练过程中在多个噪声水平上的去噪分数匹配和在采样过程中使用退火的朗之万动力学的等价性”
这种等价性指的是?introduction中说这是他的最大贡献
首先,设定方差为不可学习;
其次,为了表示平均µθ(xt,t),我们提出了一个特定的参数化,由以下的Lt分析驱动。使用pθ(xt−1|xt)=N(xt−1;µθ(xt,t),σt 2 I),我们可以写:
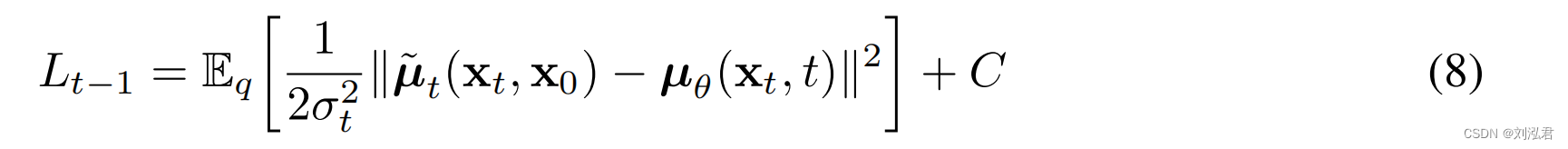
因此,我们可以看到µθ最直接的参数化是一个预测˜µt的模型,即正向过程的后验均值。但是,我们可以扩展等式(8)进一步通过重新参数化等式(4)如xt(x0,)=√¯αtx0+√1−¯αtfor∼N(0,I),并应用前向过程后向公式(7):
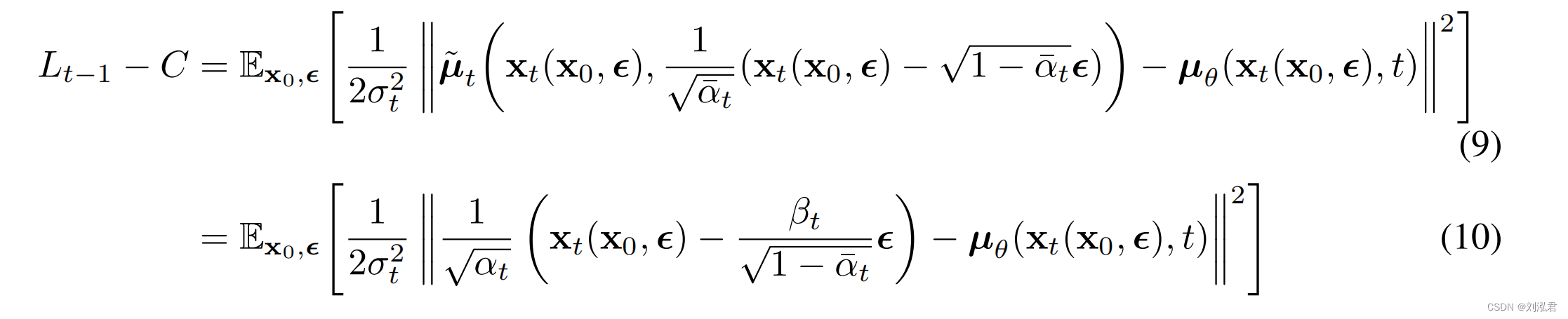

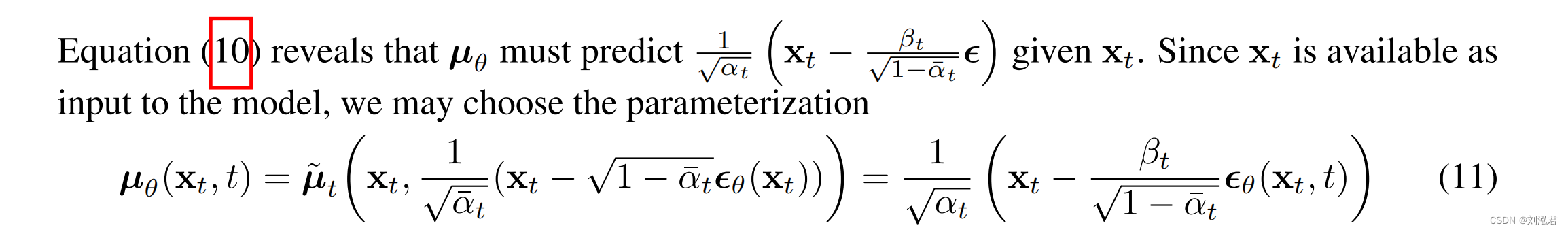
其中εθ是一个用来从xt预测epsilon的函数近似器。
这个epsilon是可学习的吗?它是指啥?N是啥?
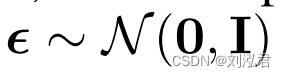

![[附源码]Node.js计算机毕业设计黑格伯爵国际英语贵族学校官网Express](https://img-blog.csdnimg.cn/ea11f0c2b11345ff950825ba5fb52fe0.png)