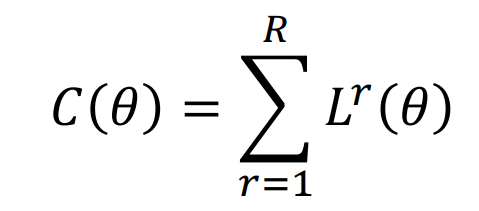M-P_神经元模型、激活函数、神经网络结构、学习网络参数、代价定义
文章目录
- M-P_神经元模型、激活函数、神经网络结构、学习网络参数、代价定义
- M-P 神经元模型
- 激活函数(Activation function)
- 神经网络结构
- 举例
- 训练神经网络
- 学习网络参数
- 代价定义
- 均方误差
- 交叉熵(Cross Entropy)
- 总代价
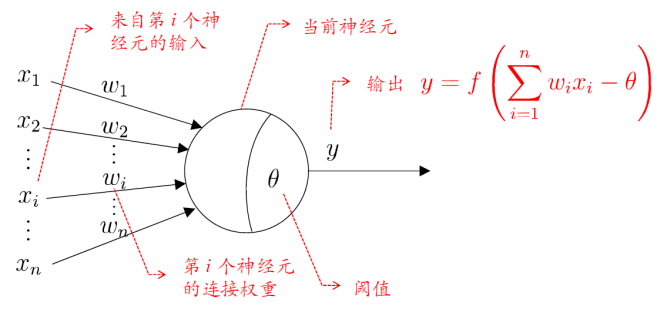
M-P 神经元模型
⚫ 输入:来自其它n个神经元传递过来的输入信号
⚫ 处理:输入信号通过带权重的连接进行传递, 神经元接受到总输入值将与神经元的阈值进行比较
⚫ 输出:通过激活函数的处理以得到输出
激活函数(Activation function)
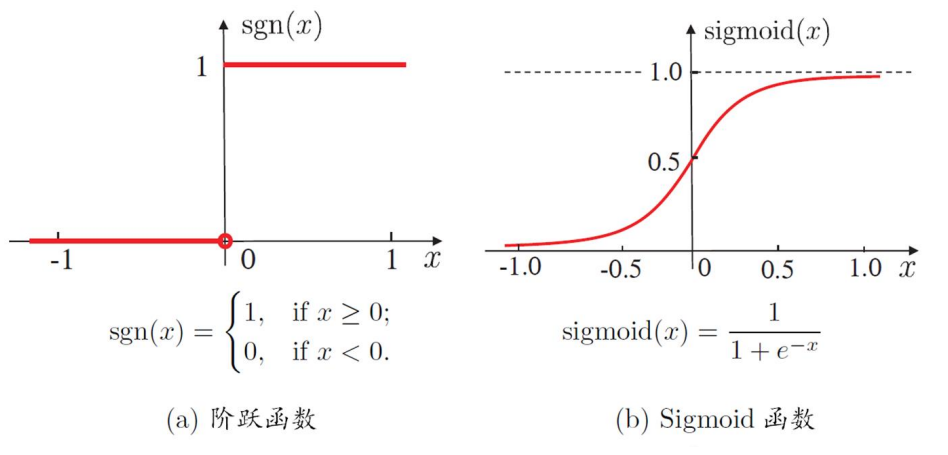
⚫ 理想激活函数是阶跃函数, 0表示抑制神经元而1表示激活神经元
⚫ 阶跃函数具有不连续、不光滑等不好的性质, 常用的是 Sigmoid 函数
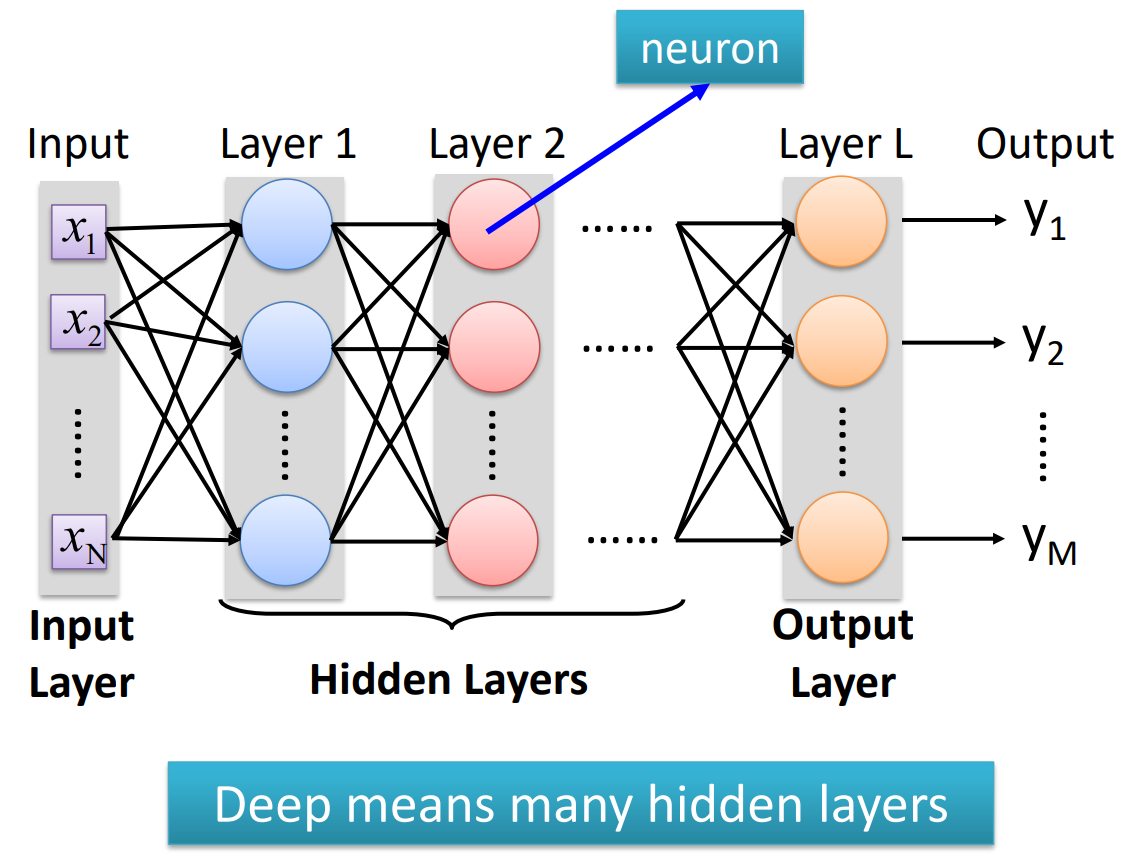
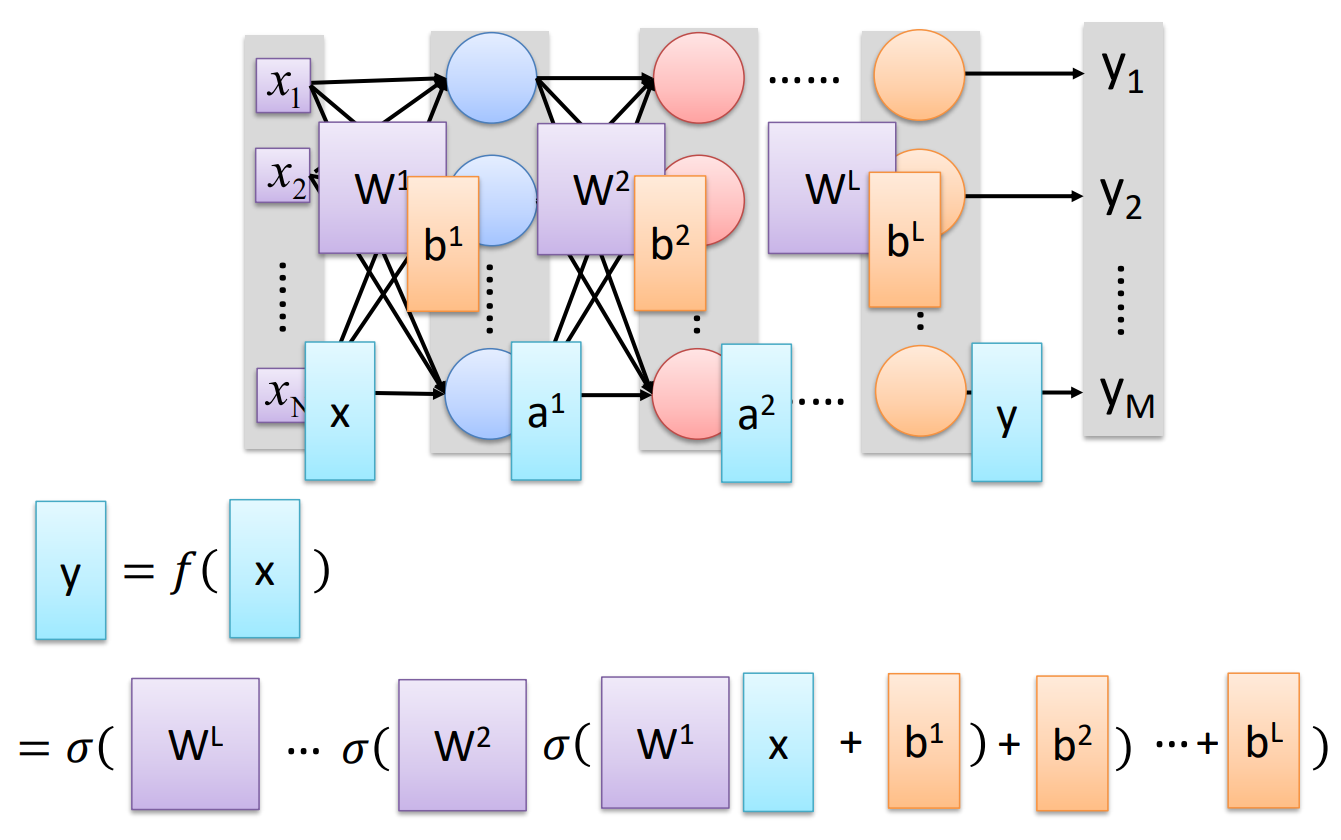
神经网络结构
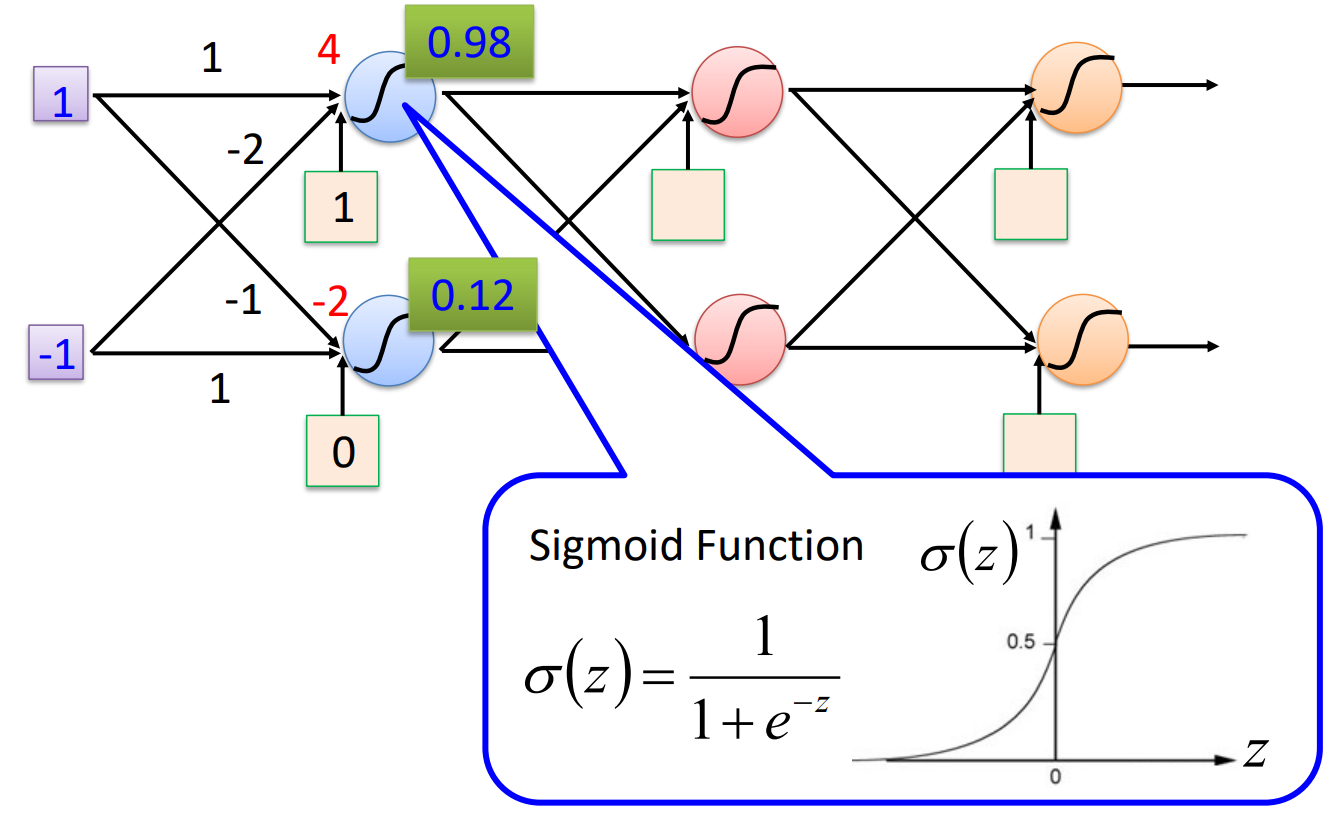
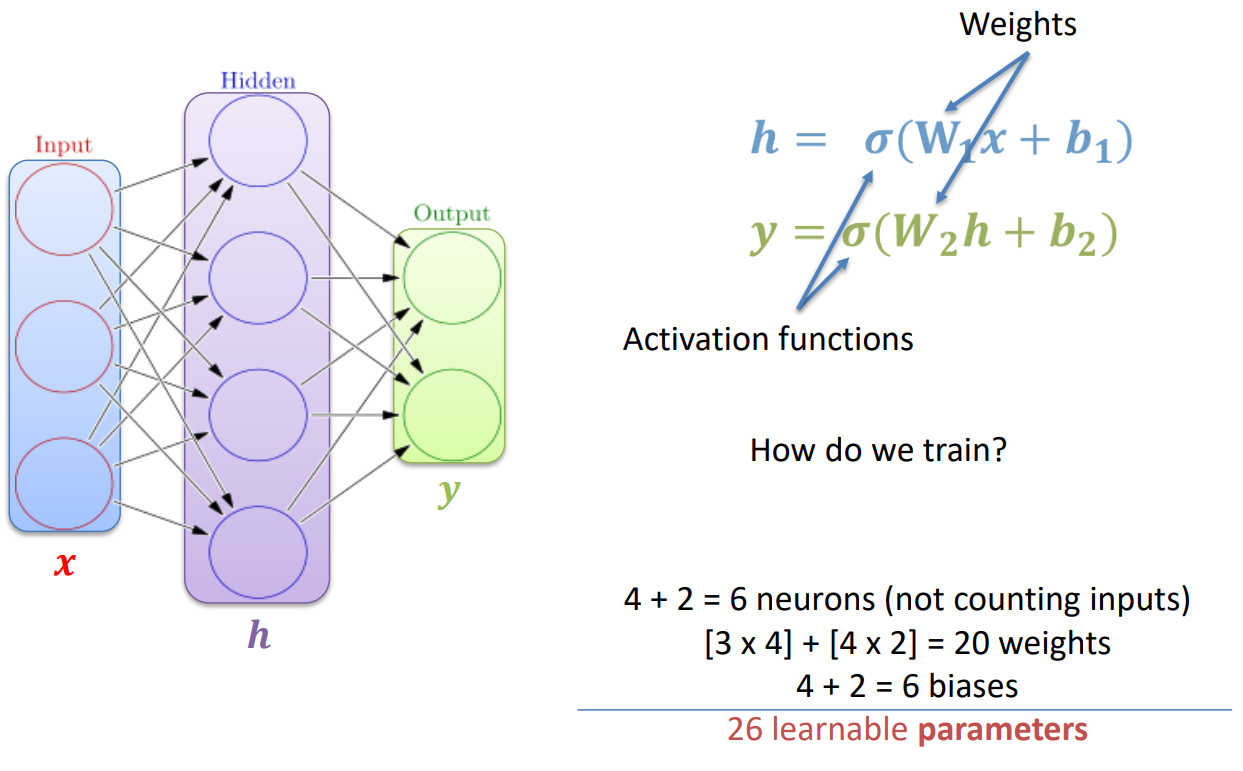
举例
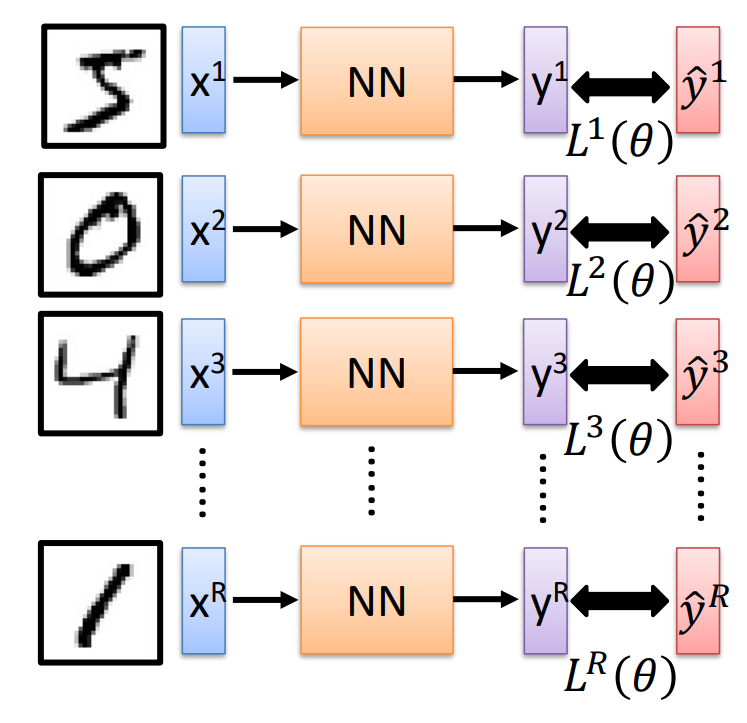
训练神经网络
学习网络参数
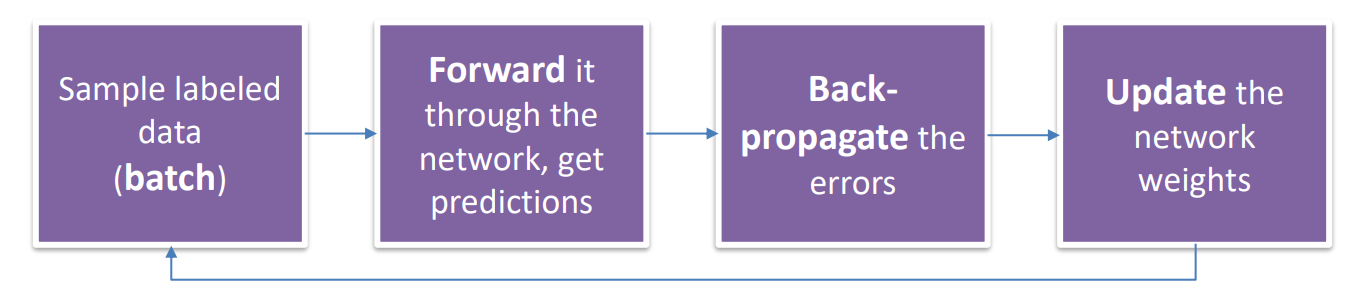
- 使用标记的样本数据(批量)
- 将其输入神经网络,获取预测结果
- 反向传播误差
- 更新神经网络的权重
这是神经网络训练的基本步骤。首先,将一批标记的样本数据输入到神经网络中,通过前向传播计算得到预测结果。然后,通过与真实标签进行比较,计算出预测结果与真实结果之间的误差。接下来,使用反向传播算法将误差从输出层向后传播,逐层计算并更新每个神经元的梯度和权重。最后,根据更新后的权重继续进行下一轮的训练,不断迭代优化神经网络的性能,直到达到预定的停止条件。
代价定义
成本函数(Cost)的定义可以是网络输出与目标之间的欧氏距离或交叉熵。
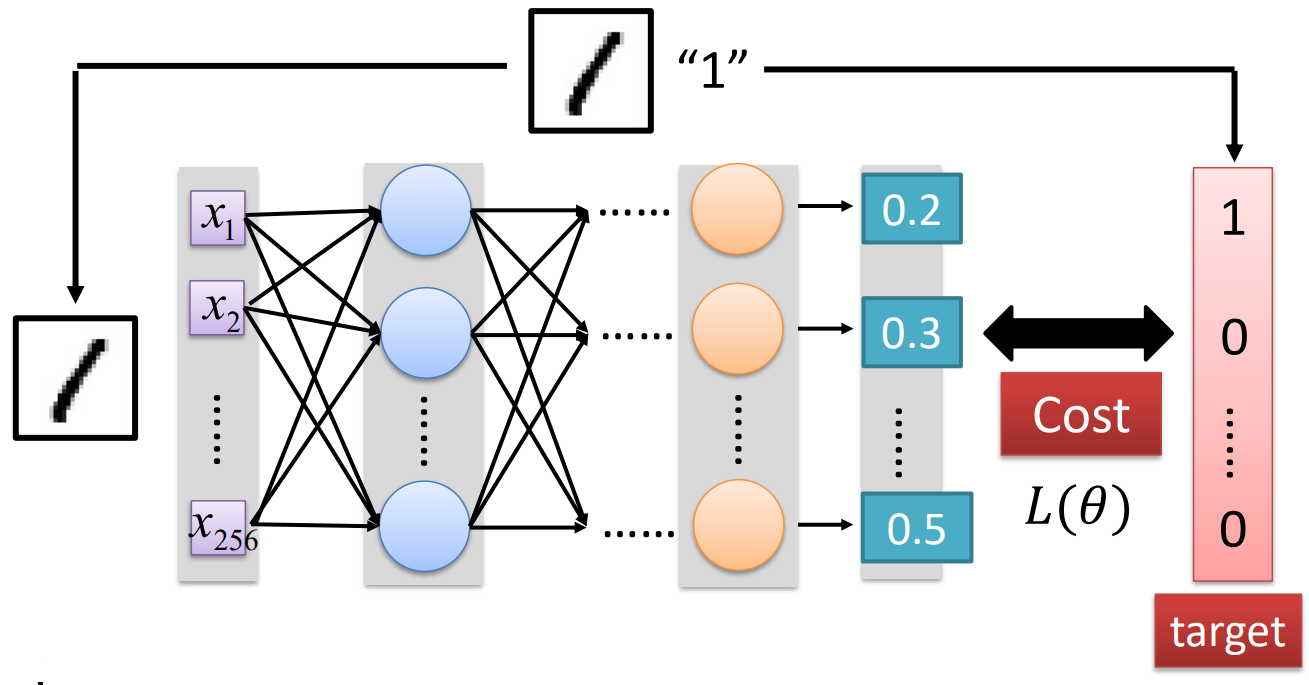
在神经网络训练中,成本函数用于衡量神经网络的预测结果与真实标签之间的差异。成本函数的选择取决于具体的任务和网络结构。
均方误差
欧氏距离也称为均方误差(Mean Squared Error,MSE)。它计算预测结果与真实标签之间的差的平方的平均值。
交叉熵(Cross Entropy)
交叉熵特别适用于分类问题。对于每个样本,成本函数的计算公式为:
C o s t = − ( 1 / N ) ∗ Σ ( y t r u e ∗ log ( y p r e d ) + ( 1 − y t r u e ) ∗ log ( 1 − y p r e d ) ) Cost = -(1/N) * Σ (y_{true}* \log(y_{pred}) + (1 - y_{true}) * \log(1 - y_{pred})) Cost=−(1/N)∗Σ(ytrue∗log(ypred)+(1−ytrue)∗log(1−ypred))
其中,N是样本数量,y_pred是神经网络的预测结果(经过激活函数处理),y_true是真实标签。
总代价
总成本(Total Cost)衡量了神经网络参数 𝜃 在该任务上的拟合程度或性能表现的好坏。
在神经网络训练中,我们通过最小化总成本来寻找最优的参数 𝜃。