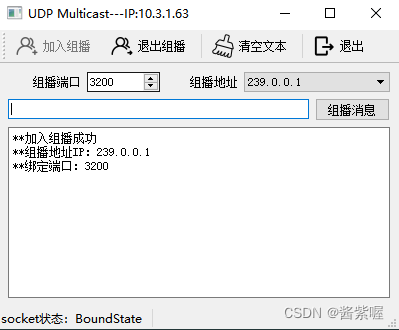
目录
题目:
示例:
分析:
代码:
题目:

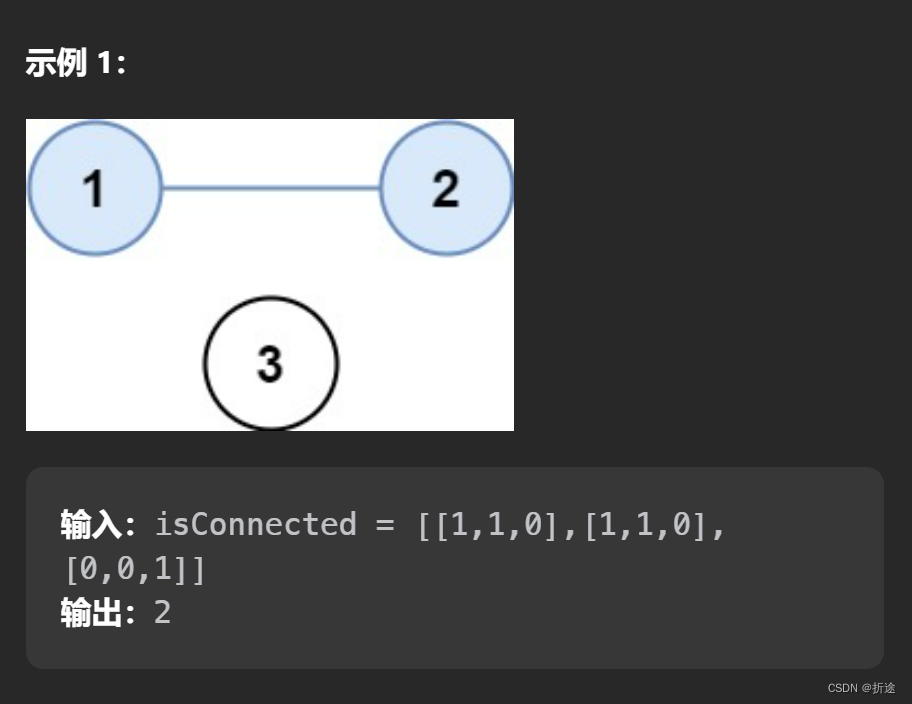
示例:
分析:
给我们一个二维数组,表示城市之间的连通情况,连在一起的城市为一个省份,问我们一共有多少个省份。
这是一道很经典很纯粹的并查集题目。按照我自己的话来说,并查集就是给将相连的元素都设置一个共同的源头,在本题中,我们让相连的城市都有一个共同的源头,那么最后我们统计一下所有城市一共有多少个不同的源头即可确定是有多少个城市了。
这代码就是很标准的并查集模板,大家记住并且理解即可。
首先我们需要定义一个长度和城市数量一样的数组,用来存放每个城市的源头。
并且需要将每个城市的源头初始化成自己。
接着遍历城市之间的连通情况。如果城市之间是连通的,那么我们需要将他们联系在一起,即把他们的源头改成同一个。
首先是先找出他们各自的源头,再把其中一个的源头的源头改成对方的源头。其中找出各自源头这一步是不断寻找源头列表里对应位置,如果一个城市的源头不是自己,那么我们就接着找这个城市的源头的源头,直到找到源头是自己的城市,那么这座城市就是我们需要寻找的城市的最终源头。
这对应了代码中的find函数。
记录完所有城市的连通情况之后,我们再看看所有城市一共有几个最终源头,将最终源头的数量返回出去即可。
代码:
class Solution {
public:
int find(int c,vector<int>& city){ //寻源
if(c==city[c]) return c; //自己就是源头,直接返回
city[c]=find(city[c],city); //接着往上寻找源头
return city[c];
}
void join(int i,int j,vector<int>& city){ //添加关系
i=find(i,city);
j=find(j,city);
if(i==j) return; //如果源头一样return
city[i]=j; //源头不一样就添加为一样,这边改成city[j]=i也是可以的
}
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int>city(isConnected.size()); //用来记录每个城市的源头
for(int i=0;i<isConnected.size();i++) city[i]=i; //初始化成每个城市都是自己的源头
for(int i=0;i<isConnected.size();i++){
for(int j=0;j<isConnected.size();j++){
if(isConnected[i][j]==1) join(i,j,city); //如果城市间是相连的,则添加关系为源头一致
}
}
//统计所有城市一共有多少个源头
unordered_set<int>res;
for(int& c:city){
res.insert(find(c,city));
}
return res.size();
}
};