题目

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

• 选择二叉树中 任意 节点和一个方向（左或者右）。
• 如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
• 改变前进方向：左变右或者右变左。
• 重复第二步和第三步，直到你在树中无法继续移动。

交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。

请你返回给定树中最长 交错路径 的长度。

示例 1：

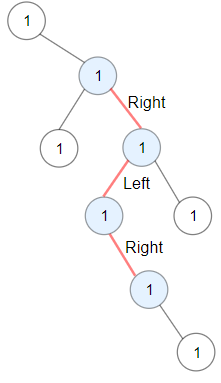
输入：root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
输出：3
解释：蓝色节点为树中最长交错路径（右 -> 左 -> 右）。

示例 2：

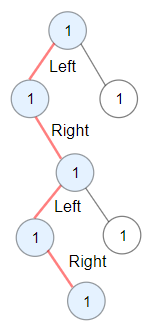
输入：root = [1,1,1,null,1,null,null,1,1,null,1]
输出：4
解释：蓝色节点为树中最长交错路径（左 -> 右 -> 左 -> 右）。

示例 3：

输入：root = [1]
输出：0

题解

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int maxlen;
    public int longestZigZag(TreeNode root) {
        if (root == null) {
            return 0;
        }
        dfs(root.left, 1, 1);
        dfs(root.right, 1, 2);
        return maxlen;
    }
    //定义一个int类型 1为左 2为右
    private void dfs(TreeNode root, int cnt, int direct) {
        if (root == null) {
            return;
        }
        maxlen = Math.max(maxlen,cnt);
        //如果没有调转方向 cnt归1
        dfs(root.left, direct == 1 ? 1 : cnt + 1, 1);
        dfs(root.right, direct == 2 ? 1 : cnt + 1, 2);
    }
}