（leetcode802，拓扑排序，深搜+三色标记）找到最终的安全状态-------------------Java实现

题目表述

有一个有 n 个节点的有向图，节点按 0 到 n - 1 编号。图由一个索引从 0 开始的 2D 整数数组 graph表示， graph[i]是与节点 i 相邻的节点的整数数组，这意味着从节点 i 到 graph[i]中的每个节点都有一条边。

如果一个节点没有连出的有向边，则该节点是终端节点。如果从该节点开始的所有可能路径都通向终端节点，则该节点为安全节点。

返回一个由图中所有安全节点组成的数组作为答案。答案数组中的元素应当按升序排列。

样例

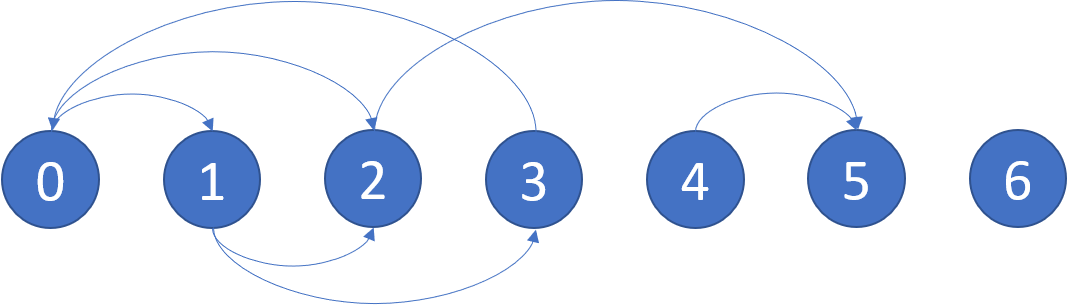
在这里插入图片描述
(上图)输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出：[4]

条件

n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
0 <= graph[i][j] <= n - 1
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 $1,4*10^4]$ 内。

思路

1、答案学习思路：深搜+三色标记法。主要思路是，根据边深搜，递归查询，发现环路之后，整条路上的其实都可以认定为不安全结点。只有所有的边都通往安全节点才是安全节点。
2、拓扑排序(容易想到)

注意点

ac代码

Java:

package leetcode802;

import java.util.*;

class Solution802 {   //拓扑排序
    public List<Integer> eventualSafeNodes(int[][] graph) {

        Set<Integer>[] Source_graph = new HashSet[graph.length];
        int[] Target_graph = new int[graph.length];
        List<Integer> result = new ArrayList<>();
        for (int i=0;i<graph.length;i++) {
            Source_graph[i] = new HashSet<>();
            Target_graph[i] = graph[i].length;
        }
        for (int i=0;i< graph.length;i++)
        for (int j=0;j<graph[i].length;j++)
            Source_graph[graph[i][j]].add(i);
        Queue<Integer> q = new ArrayDeque<>();
        for (int i=0;i<Target_graph.length;i++) {
            if (Target_graph[i]==0) {
                q.offer(i);
                result.add(i);
            }
        }
        while(!q.isEmpty()){
            int now_source = q.poll();
            for (Integer i :Source_graph[now_source])
            {
                Target_graph[i]--;
                if (Target_graph[i]==0)
                {q.offer(i);result.add(i);}
            }
        }
        Collections.sort(result);

    return result;
    }
}
class Solution802_2 {  //深搜+三色标记
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int[] color = new int[graph.length];
        List<Integer> ans = new LinkedList<Integer>();
        for (int i=0;i<graph.length;i++)
            if (safe(graph,color,i))
                ans.add(i);
    Collections.sort(ans);
    return ans;
    }
    public boolean safe(int[][] graph,int[] color,int x)
    {
        if (color[x]!=0)
            return color[x]==2;
        color[x] = 1;
        for (int i:graph[x])
            if (!safe(graph,color,i))
                return false;
        color[x] = 2;
        return true;
    }
}
public class leetcode802 {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int n = cin.nextInt();
        cin.nextLine();
        int[][] graph = new int[n+1][];
        for (int i =0;i<=n;i++){
            String line = cin.nextLine();
            if (line.isEmpty()) {
             graph[i] = new int[0];
                continue;
            }
            String[] numbers = line.split(" ");
            graph[i] = new int[numbers.length];
            for (int j=0;j<numbers.length;j++)
                graph[i][j] = Integer.parseInt(numbers[j]);

            }
    cin.close();
//        Solution802 s = new Solution802();
        Solution802_2 s_2 = new Solution802_2();
//        System.out.println(s.eventualSafeNodes(graph));
        System.out.println(s_2.eventualSafeNodes(graph));
        // input
//        6
//        1 2
//        2 3
//        5
//        0
//        5



    }
}