《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 简化农场” ,链接: http://oj.ecustacm.cn/problem.php?id=1879
题目描述
【题目描述】 约翰的农场可以看做一个图,农田代表图中顶点,田间小路代表图中的边,每条边有一定的长度。
约翰发现自己的农场中最多有三条小路有着相同的长度。
约翰想删除一些小路使得农场成为一棵树,使得两块农田间只有一条路径。
约翰想把农场设计成最小生成树,也就是农场道路的总长度最短。
请帮助约翰找出最小生成树的总长度,同时请计算出总共有多少种最小生成树。
【输入格式】 输入第一行为两个正整数 N 和 M ,表示点数和边数(1 <= N <= 40,000; 1 <= M <= 100,000)。
接下来 M 行,每行三个整数 ai, bi, ci,表示点 ai 和 bi 之间存在长度为 ci 的无向边。(1 <= ai, bi <= N; 1 <= ci <= 1,000,000)
【输出格式】 输出一行包含两个整数,分别表示最小生成树的长度和最小生成树的数目。
数目对 1,000,000,007 求余.
【输入样例】
4 5
1 2 1
3 4 1
1 3 2
1 4 2
2 3 2
【输出样例】
4 3
题解
有两种最小生成树(MST)算法:kruskal、prim。Kruskal的思路是对边贪心,“最短的边一定在MST上”;prim的思路是对点贪心,“最近的邻居点一定在MST上”。
本题描述中比较特殊的地方是:(1)最多有三条小路(边)有相同长度;(2)计算总共有多少种最小生成树。着重点在边上,所以用kruskal算法。
kruskal算法执行步骤是:(1)对边排序;(2)从最短的边开始,从小到大依次把边加入到MST中;(3)加边的过程中用并查集判断是否产生圈,如果形成了圈就丢弃这个边;(4)所有边处理完后结束,或者加边的数量等于n-1时结束。
如果所有的边长都不同,那么只有一种最小生成树。题目指出“最多有三条边的长度相同”,从样例可知,有等长的两条边,也有等长的三条边。对边排序时,这些相等的边会挨在一起。
处理等长边,设cnt是合法(所谓合法,是指这个边加入到MST,不会产生圈)的边的数量,num是这几个等长边有几个能同时加入到MST。sum是最小生成树的数目。
(1)有两条等长边。
若cnt=1,只有一条边是合法的,也就是说这条边别无选择,那么sum不变。
若cnt=2,有2条边合法,继续讨论:
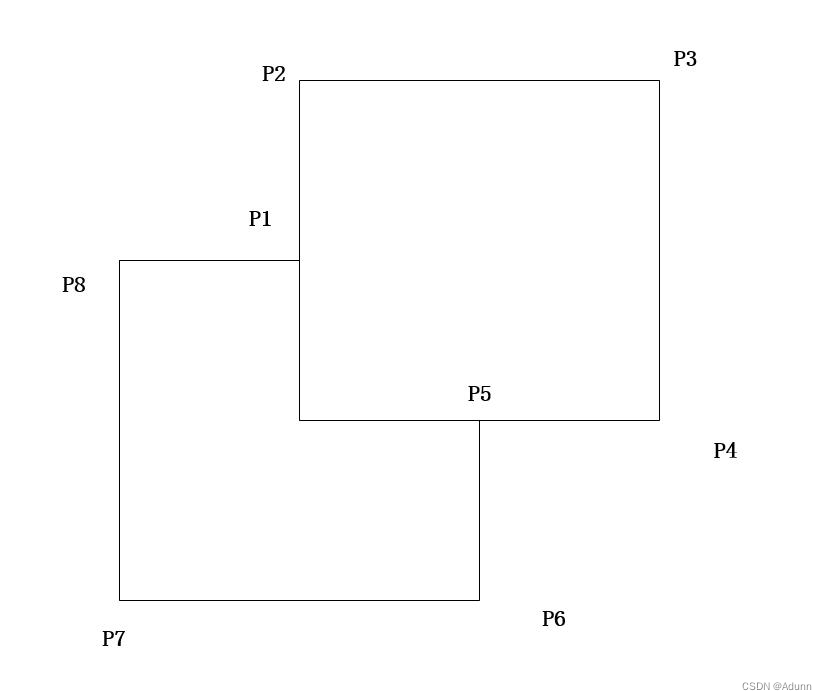
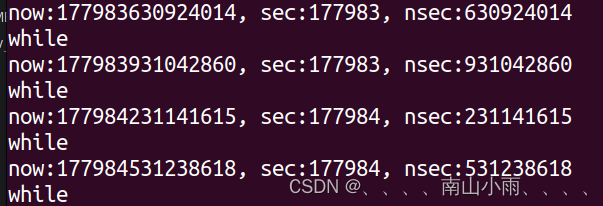
1)num=1,即这两条等长边只有一条能加入到MST中。那么sum = sumcnt,即sum=sum2。以下图为例,s1和s2是两棵已经加入到MST的子树,它们内部没有圈。现在加两条等长边(x1,y1)、(x2,y2),它们单独加入MST都是合法的,但是同时加入就会形成圈。
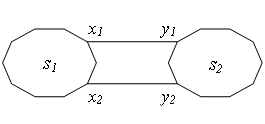
2)num=2,即这两条等长边都应该加入到MST中。那么sum不变,即sum=sum1。以下图为例。
(2)有三个等长边。
若cnt=1,只有一条边合法,sum不变。
若cnt=2,有两条边合法,和(1)有两条等长边,且cnt=2的情况一样。
若cnt=3,有三条边合法,那么:
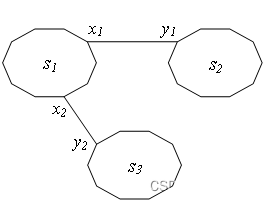
1)num = 1,只有一条边能加入到MST中,sum = sumcnt=sum3。以下图为例,三条边任选一条,有3种情况。
2)num = 2,有两条边能加入到MST中,且其中一条边必须加,sum = sum2。以下图为例,三条边任选两条,有2种情况。
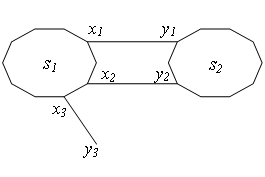
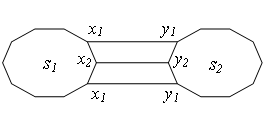
3)num = 2,有两条边能加入到MST中,且是任意两条,sum = sum*3。以下图为例,三条边任选两条,有3种情况。
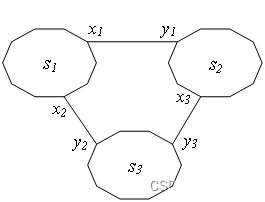
3)num = 3,三条边都应该加入到MST中,sum不变。
【重点】 kruskal 。
C++代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+10;
const int mod = 1e9+7;
struct Node{int x,y,val;}e[N<<1];
bool cmp(Node a,Node b){return a.val<b.val;}//按边权排序
int n,m;
int s[N]; //并查集
int ans=0,sum=1; //ans: MST的总长度, sum:最小生成树的数目
int find_set(int x){ //查询并查集,返回x的根
if(x != s[x]) s[x] = find_set(s[x]); //路径压缩
return s[x];
}
void kruscal(){
for(int i=1;i<=n;i++) s[i] = i; //并查集初始化
sort(e+1,e+m+1,cmp); //边:升序排序
for(int i=1;i<=m;){ //遍历所有边,每次处理其中的等长边
int cnt = 0; //这次的等长边中,有几个可以加入MST
set<pair<int,int> >st; //set用于存储并去重
int j; //第i~j个边等长
for(j=i;j<=i+2 && e[i].val==e[j].val;j++){ //枚举等长边,最多3个相同。更新j
int s1 = find_set(e[j].x); //边的一个端点属于哪个集?
int s2 = find_set(e[j].y); //边的另一个端点属于哪个集?
if(s1 > s2) swap(s1,s2);
if(s1 != s2){ //两个集不等,这个边可以加入到MST中
cnt ++; //cnt: 允许加入MST的边的数量
st.insert(make_pair(s1,s2)); //这个边的两端点所属的集存到st中
}
} //第i~j个边是等长的
int num = 0;
for(;i<j;i++){ //开始时第i~j个边是等长的。i=j时退出
int s1 = find_set(e[i].x);
int s2 = find_set(e[i].y);
if(s1 != s2){ //不属于一个集,可以加入到树里
s[s2] = s1; //并查集合并
num++; //这几个等长边有num个可以同时加入树
}
}
ans += e[i-1].val*num; //这几个等长边最后有num个可以加入到MST,计算MST总长
if(num == 1) sum = sum*cnt%mod; //只有一条边能加入树,直接乘以cnt
if(cnt == 3 && num==2 && st.size() == 2) sum = 2*sum%mod;
if(cnt == 3 && num==2 && st.size() == 3) sum = 3*sum%mod;
//其他情况方案数都不变
}
}
signed main(){
scanf("%lld%lld",&n,&m); //读点,边
for(int i=1;i<=m;i++) //存边,用最简单的“边集数组”存边
scanf("%lld%lld%lld",&e[i].x,&e[i].y,&e[i].val);
kruscal(); //最小生成树
printf("%lld %lld\n",ans,sum);
}
Java代码
Python代码