目录

题目：

示例：

分析：

代码：

---

题目：

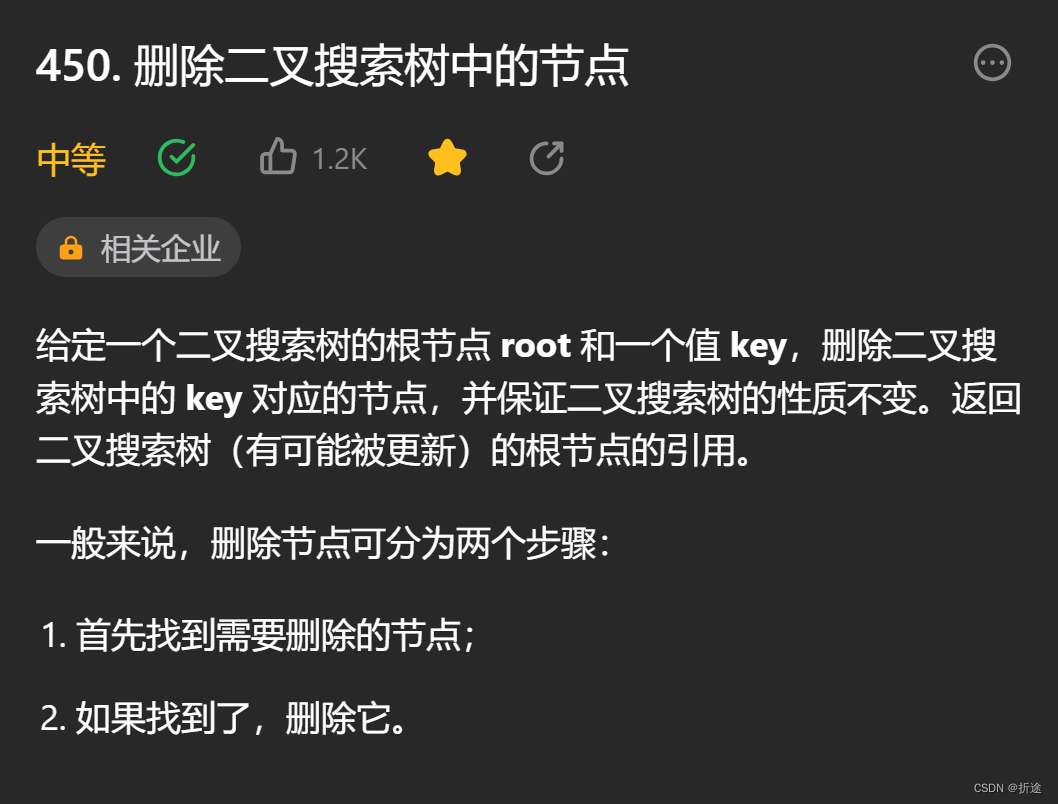
示例：

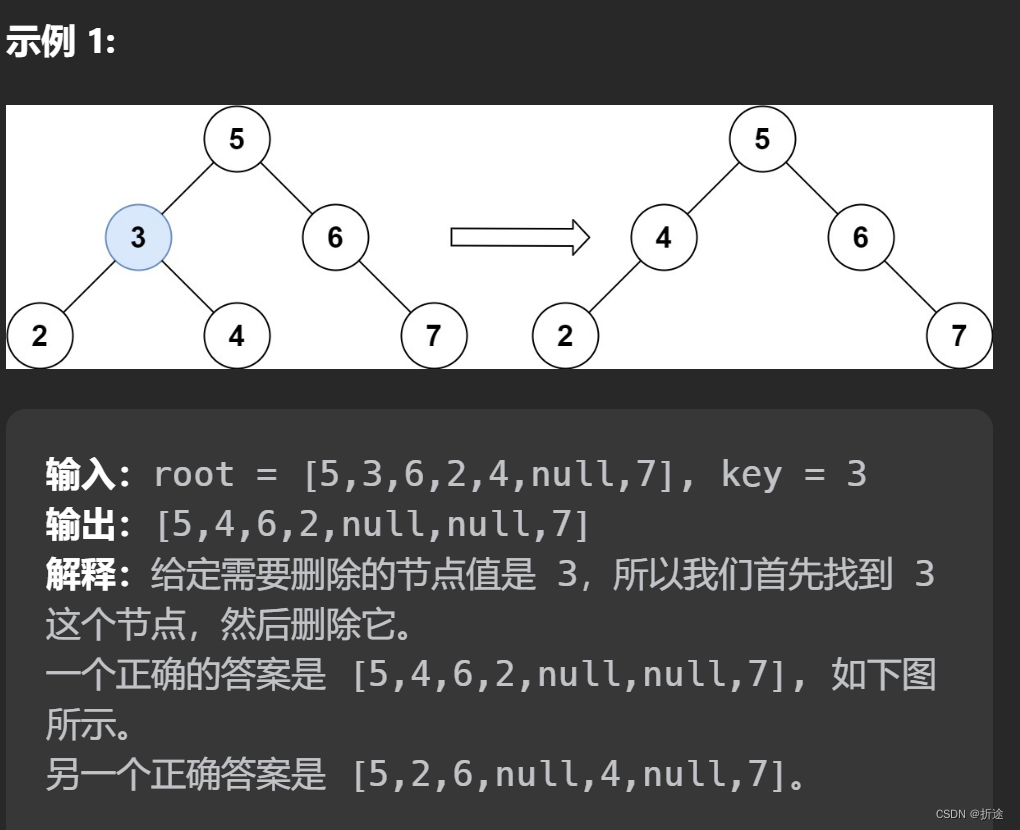
分析：

题目给我们一棵二叉搜索树，给我们一个目标值，让我们删除节点值等于目标值的节点，并且删除之后需要保持二叉搜索树的定义，也就是任意一个节点的左子树上的所有节点的值都小于该节点的值，右子树上的所有节点的值都大于该节点的值。

删除一个节点我们首先需要先找到这个节点，根据二叉搜索树的定义，我们遍历二叉树，如果当前节点的值大于目标值，那么目标值只能存在与当前节点的左子树，我们就接着向左子树遍历，反之向右子树遍历。

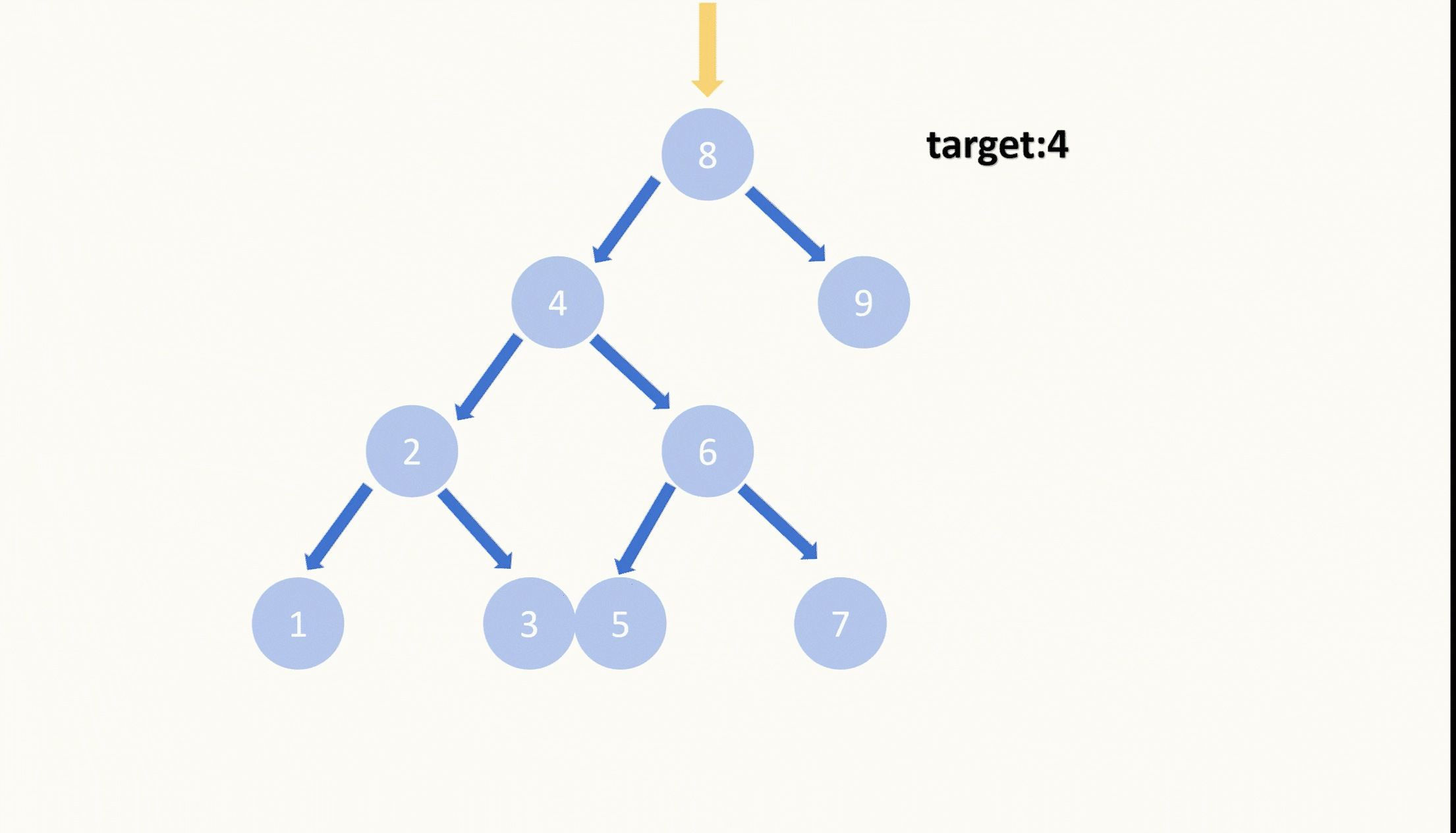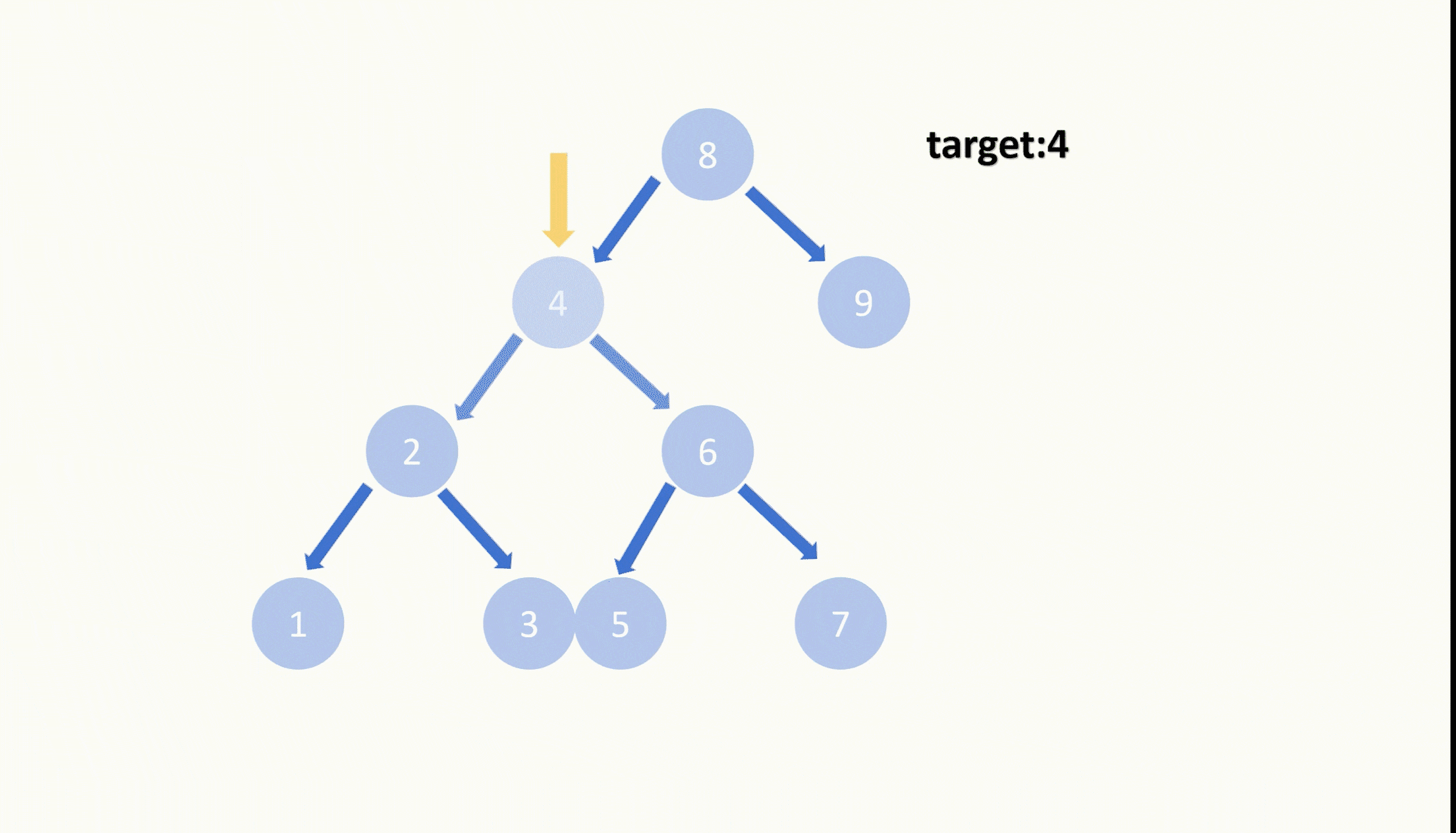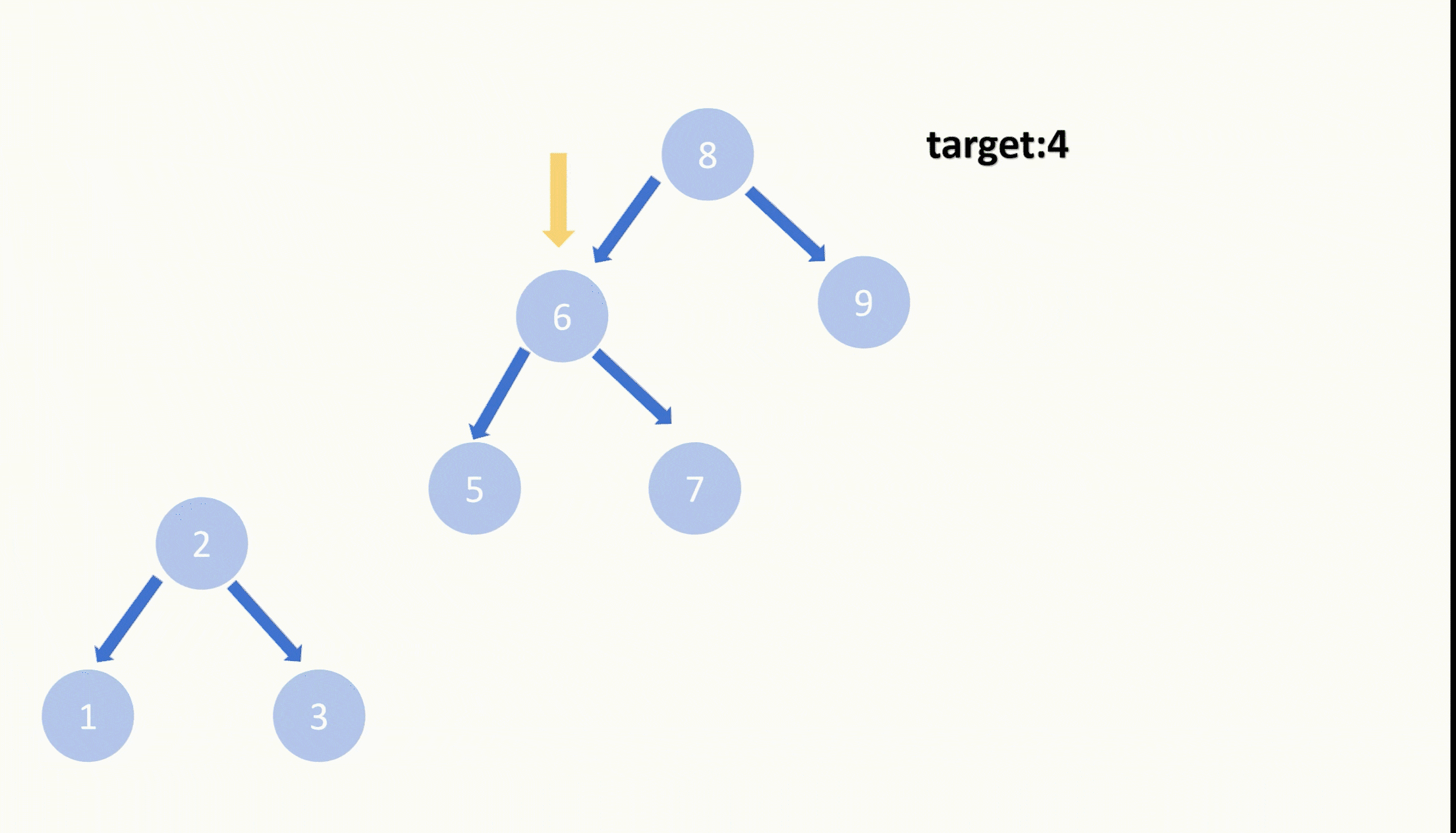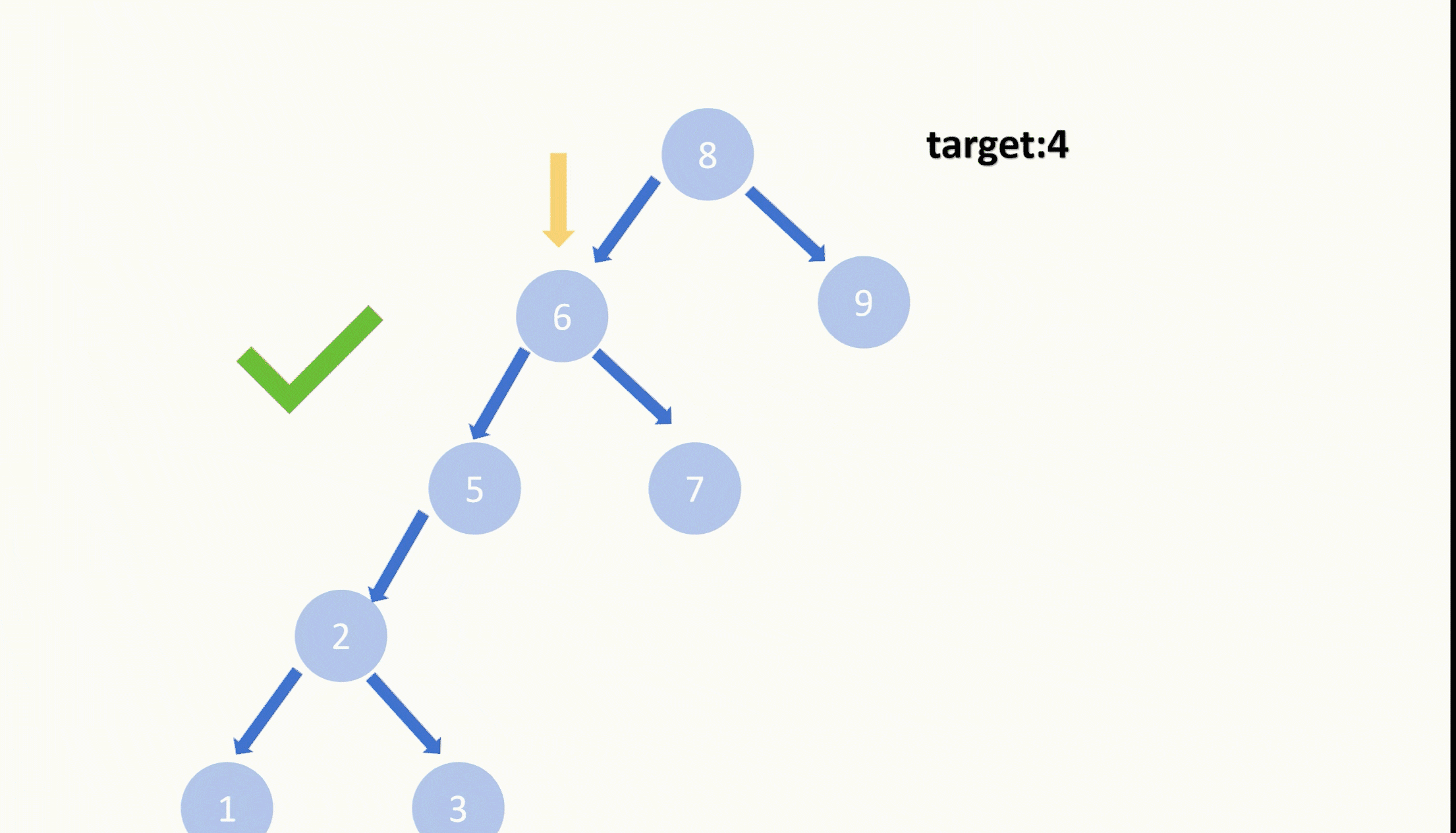
直到我们找到了目标节点，我们需要把它删除，并且还需要保持这是一棵二叉搜索树。我们可以知道目标节点的右子树上任意一个节点的值都比目标节点的左子树上任意一个节点的值更大，所以我们可以把目标节点的右子树接到目标节点的左子树的最大的节点的右子树上，再让目标节点的左子树顶替上原先目标节点的位置，这样就完成了删除目标节点的这样的操作。

我们也可以是让目标节点的右子树顶替上原先目标节点的位置，再在右子树里最小的节点的左子树接上目标节点的左子树，这样也是可以的。都是满足二叉搜索树的定义。

代码：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root==nullptr) return root;
        if(root->val==key){
            if(root->right==nullptr) return root->left;
            if(root->left==nullptr) return root->right;
            TreeNode* node=root->left;
            while(node->right) node=node->right;
            node->right=root->right;
            root=root->left;
        }else if(root->val<key) root->right=deleteNode(root->right,key);
        else if(root->val>key) root->left=deleteNode(root->left,key);
        return root;
    }
};